微分ランダム問題集

【難易度★】
　高校数学の教科書の基本的な例題レベルの難易度です。
　基本を理解できているかのチェックをしたい方向けです。

【難易度★★】
　高校数学の教科書の演習・章末問題のレベルの難易度です。
　数学の定期試験の対策がしたい方向けです。

【難易度★★★】
　高校数学の教科書の問題と比べ、やや難しい難易度です。
　入試問題の基礎的なレベルの問題を解きたい人向けです。

【ランダムに出題】
従来の問題集では、問題の種類ごとに整理されている形式が一般的であるため、解き始める前に『解法のパターン』を分かった上で解くことになります。

そのため、従来の問題集では問題文から解法を見抜く力を養うことができないという欠点があります。

本問題集では、問題をランダムに出題することで定期テスト・入試問題で必須となる "問題文から解法を見抜く力" が付くように意図しています。

また、本ページの下部に問題の一覧も掲載しているため、通常の問題集としても活用できます。

【ヒントボタン】
本問題集では、問題の下のヒントボタンを押すことで解答のヒントが見れるようにしています。

『自力で解けそうな場合はヒントなしで解く』、『手も足も出ない場合にヒントを見る』とすることで "段階的にレベルアップ" できることを意図しています。

【問題数】
本問題集では、高校数学Ⅱ・Ⅲの微分に関連する問題を98問掲載しています。

【平均変化率・導関数の定義】

問題1 : 関数$\hspace{2pt}f(x)=ax^2+1\hspace{2pt}$の${\hspace{2pt}x=1\hspace{2pt}}$から${\hspace{2pt}x=3\hspace{2pt}}$における平均変化率が$\hspace{1pt}12\hspace{1pt}$であるとき、$\hspace{1pt}a\hspace{1pt}$の値を求めよ

問題2 : 関数$\hspace{2pt}f(x)=2x^2-3x\hspace{2pt}$の${\hspace{2pt}x=1\hspace{2pt}}$における微分係数を定義に従って求めよ

問題3 : 関数$\hspace{2pt}y=x^2-x\hspace{2pt}$の導関数を定義に従って求めよ

問題4 : 関数$\hspace{2pt}y=2x^3+4\hspace{2pt}$の導関数を定義に従って求めよ

問題5 : $f(x)+x f'(x) = 2x^2 +x -1\hspace{3pt}$を満たす二次関数$\hspace{2pt}f(x)\hspace{2pt}$を求めよ

【接線の方程式】

問題6 : $\displaystyle y=\frac{1}{3}x^3-4x\hspace{3pt}$上に接点を持つ、傾きが$\hspace{1pt}5\hspace{1pt}$の接線の方程式を求めよ

問題7 : 点$\hspace{1pt}(2,-4)\hspace{1pt}$から関数$\displaystyle\hspace{1pt}y=-\frac{1}{3}x^3-x-2\hspace{3pt}$に引いた接線の方程式を求めよ

【最大値・最小値】

問題8 : 関数$\hspace{1pt}y=x^3+3x^2 -9x-5\hspace{3pt}$の区間$\hspace{1pt}-4 \leqq x \leqq 2\hspace{1pt}$における最大値・最小値を求めよ

【三次関数のグラフ】

問題9 : 関数$\hspace{1pt}y=2x^3-6x\hspace{2pt}$のグラフをかけ

問題10 : 関数$\hspace{1pt}y=-x^3+3x^2+9x+5\hspace{2pt}$のグラフをかけ

問題11 : 関数$\hspace{1pt}y=|x^3 -3x^2 +2|\hspace{2pt}$のグラフをかけ

【三次方程式】

問題12 : 方程式$\hspace{3pt}x^3+3x^2-4=0\hspace{2pt}$の実数解の個数を求めよ

問題13 : 方程式$\hspace{3pt}x^3-6x+4=0\hspace{2pt}$の実数解の個数を求めよ

【三次不等式】

問題14 : $\hspace{1pt}x \geqq 0\hspace{1pt}$のとき、不等式$\hspace{3pt}2x^3-6x^2+8 \geqq 0\hspace{2pt}$が成り立つことを証明せよ

問題15 : $\hspace{1pt}x \geqq 0\hspace{1pt}$のとき、不等式$\hspace{3pt}x^3 \geqq 3x^2 -4\hspace{2pt}$が成り立つことを証明せよ

【平均変化率・導関数の定義】

問題1 : $\displaystyle \hspace{3pt}\lim_{h \rightarrow 0}{ \frac{f(a+2h) - f(a-4h)}{h}}\hspace{4pt}$を$\hspace{3pt}f'(a)\hspace{2pt}$で表せ

【三次関数への応用】

問題2 : 関数$\hspace{1pt}y=ax^3+bx^2 +cx\hspace{3pt}$が$\hspace{1pt}x=-2\hspace{1pt}$で極大値、$\hspace{1pt}x=1\hspace{1pt}$で極小値、極大値と極小値の差が$\hspace{1pt}27\hspace{1pt}$であるとき、定数$\hspace{1pt}a,b,c\hspace{1pt}$を求めよ

問題3 : 関数$\hspace{1pt}y=2x^3 + ax^2 + x -1\hspace{1pt}$が常に増加するための定数$\hspace{1pt}a\hspace{1pt}$の条件を求めよ

問題4 : 関数$\hspace{1pt}y=x^3 + ax^2 - ax +2\hspace{1pt}$が極値を持つための定数$\hspace{1pt}a\hspace{1pt}$の条件を求めよ

【最大値・最小値】

問題5 : 関数$\hspace{2pt}y=2x^3 -3ax^2+b\hspace{2pt}$の$\hspace{2pt} 0 \leqq x \leqq 1\hspace{1pt}$における最大値・最小値を求めよ。ただし、$a > 0\hspace{2pt}$とする。

問題6 : 関数$\hspace{2pt}y=-x^3 +3ax+b\hspace{2pt}$の$\hspace{2pt} 0 \leqq x \leqq 1\hspace{1pt}$における最大値・最小値を求めよ。ただし、$a > 0\hspace{2pt}$とする。

問題7 : 縦, 横, 高さの三辺の和が$\hspace{1pt}12\hspace{1pt}$であり、底面が正方形である直方体の体積の最大値を求めよ。また、そのときの三辺の長さを求めよ。

問題8 : 半径$\hspace{1pt}a\hspace{1pt}$の球に内接する直円柱の体積の最大値と、そのときの直円柱の高さを求めよ

【三次方程式】

問題9 : 方程式$\hspace{3pt}x^3 -3x^2 -9x -a=0\hspace{2pt}$の実数解の個数を求めよ

問題10 : 方程式$\hspace{3pt}-x^3 +3x+a=0\hspace{2pt}$の実数解の個数を求めよ

問題11 : 方程式$\hspace{3pt}2x^3-3x^2 -a=0\hspace{2pt}$が異なる$\hspace{1pt}3\hspace{1pt}$個の実数解を持つとき、定数$\hspace{1pt}a\hspace{1pt}$の値を求めよ

問題12 : 方程式$\hspace{3pt}x^3+3x^2 -9x-a=0\hspace{2pt}$が異なる$\hspace{1pt}2\hspace{1pt}$個の実数解を持つとき、定数$\hspace{1pt}a\hspace{1pt}$の値を求めよ

【平均変化率・導関数の定義】

問題1 : $\displaystyle \hspace{3pt}\lim_{x \rightarrow a}{ \frac{x^2 f(a)- a^2f(x)}{x^2-a^2}}\hspace{4pt}$を$\hspace{3pt}f(a),f'(a)\hspace{2pt}$で表せ

【三次関数】

問題2 : 関数$\hspace{1pt}y=x^3 + ax^2 - bx +3\hspace{1pt}$が極値を持たないための条件を求めよ。また、その極値を持たないときの$\hspace{1pt}(a,b)\hspace{1pt}$の領域を図示せよ。

【最大値・最小値】

問題3 : 関数$\hspace{2pt}y = 4 \sin^3 x + 3 \cos^2 x\hspace{3pt}$$(0 \leqq x \leqq \pi\hspace{2pt})$ の最大値と最小値を求めよ

問題4 : 関数$\hspace{2pt}y = \sin^3x + \cos^3x\hspace{4pt}$$(0 \leqq x \leqq 2\pi\hspace{2pt})$ の最大値と最小値を求めよ

問題5 : 関数$\hspace{2pt} y = 3^{3x-1} -2 \cdot 3^{2x+1} + 3^{x+3} +2\hspace{4pt}$$\hspace{1pt}(x \geqq 0 )\hspace{2pt}$の最大値と最小値を求めよ

問題6 : 縦, 横, 高さの三辺の和が$\hspace{1pt}5\hspace{1pt}$、表面積が$\hspace{1pt}16\hspace{1pt}$である直方体の体積の最小値・最大値を求めよ。また、そのときの縦,横,高さの三辺の長さを求めよ。

【三次方程式】

問題7 : 方程式$\hspace{1pt}x^3-3ax^2 +4a = 0\hspace{1pt}$の異なる実数解の個数を調べよ。ただし、$a > 0\hspace{1pt}$とする。

問題8 : 方程式$\hspace{1pt}x^3-3kx +k = 0\hspace{1pt}$が異なる$\hspace{1pt}3\hspace{1pt}$個の実数解を持つときの定数$\hspace{1pt}k\hspace{1pt}$の値を求めよ

【三次不等式】

問題9 : 不等式$\hspace{2pt}4 \cos^3 x + \sin^2 x -2 \cos x +2 \geqq 0\hspace{4pt}$$(0 \leqq x \leqq 2\pi\hspace{2pt})$ を証明せよ

問題10 : $x > 0\hspace{3pt}$のとき 不等式$\hspace{2pt}8^x + a > 3\cdot 2^{2+x} \hspace{4pt}$を満たす定数$\hspace{1pt}a\hspace{1pt}$の条件を求めよ

【導関数の定義】
　以下の関数の導関数を、定義に従って求めよ
　必要であれば$\displaystyle\hspace{2pt}\lim_{h \to 0} \frac{\sin h}{h}=1\hspace{2pt}$を用いてよい

問題1 : $\displaystyle \hspace{3pt}y=\sqrt{x}$

問題2 : $\displaystyle \hspace{3pt}y=\frac{1}{x+1}$

問題3 : $\displaystyle \hspace{3pt}y=\sin x$

問題4 : $\displaystyle \hspace{3pt}y=\cos x$

問題5 : $\displaystyle \hspace{3pt}y=\tan x$

【微分の計算】
　以下の関数を微分せよ

問題6 : $\displaystyle \hspace{3pt}y=\sqrt{x+2}(x^5+1)$

問題7 : $\displaystyle \hspace{3pt}y=\frac{x^2}{x^4+1}$

問題8 : $\displaystyle \hspace{3pt}y=\sqrt{\frac{x-1}{x+1}}$

問題9 : $\displaystyle \hspace{3pt}y=\sin^2(5x+1)$

問題10 : $\displaystyle \hspace{3pt}y=\sqrt{1+\cos x}$

問題11 : $\displaystyle \hspace{3pt}y=\sqrt[3]{x^2-2x}$

問題12 : $\displaystyle \hspace{3pt}y=\sin x \cos^3 x$

問題13 : $\displaystyle \hspace{3pt}y=\frac{1}{\tan^3 x}$

問題14 : $\displaystyle \hspace{3pt}y=\log |\sin x|$

問題15 : $\displaystyle \hspace{3pt}y=\log_2 (x^2+2x+3)$

問題16 : $\displaystyle \hspace{3pt}y=(\log (2+\sin x))^2$

問題17 : $\displaystyle \hspace{3pt}y=\frac{e^x}{x^3+1}$

問題18 : $\displaystyle \hspace{3pt}y=e^x \cos x$

問題19 : $\displaystyle \hspace{3pt}y=x^x\hspace{8pt}(x>0)$

問題20 : $\displaystyle \hspace{3pt}y=x^{\sin x}\hspace{8pt}(x>0)$

　次の方程式において$\displaystyle\hspace{1pt}\frac{dy}{dx}\hspace{1pt}$を求めよ

問題21 : $\displaystyle \hspace{3pt}\frac{x^2}{9} +\frac{y^2}{4} =1$

問題22 : $\displaystyle \hspace{3pt}x^\frac{1}{3} +y^\frac{1}{3} =1$

$x\hspace{2pt}$の関数$\hspace{2pt}y\hspace{2pt}$が媒介変数$\hspace{2pt}t\hspace{2pt}$により次の式で表されるとき, $\displaystyle\hspace{1pt}\frac{dy}{dx}\hspace{1pt}$を$\hspace{1pt}t\hspace{1pt}$の関数で表せ

問題23 : $\displaystyle \hspace{3pt}x=t^2 +2t\hspace{1pt},\hspace{3pt}y=t^3-3t+1$

問題24 : $\displaystyle \hspace{3pt}x=2(t-\sin t)\hspace{1pt},\hspace{2pt}y=2 (1-\cos t)$

問題25 : $\displaystyle \hspace{3pt}x=\frac{1-t^2}{1+t^2}\hspace{1pt},\hspace{2pt}y=\frac{2t}{1+t^2}$

【関数のグラフ】

　次の関数のグラフの凹凸,変曲点を調べてグラフをかけ

問題26 : $\hspace{1pt}y=x^4-2x^2$

問題27 : $\displaystyle\hspace{1pt}y=\frac{2x}{x^2+1}$

【最大値・最小値】
　次の関数の最大値・最小値を求めよ

問題28 : $\displaystyle\hspace{1pt}y= \frac{\sin x}{2 -\cos x} \hspace{3pt}(0 \leqq x \leqq 2\pi)$

問題29 : $\displaystyle\hspace{1pt}y= \frac{\log x}{x} \hspace{3pt}\left(\hspace{1pt}\frac{1}{e} \leqq x \leqq e^2 \right)$

【方程式への応用】
　次の方程式の実数解の個数を求めよ

問題30 : $\hspace{3pt}2 \sin x - x = 0\hspace{2pt}$$\hspace{3pt}( 0 \leqq x \leqq 2 \pi)\hspace{1pt}$

問題31 : $\hspace{3pt}x^2 e^x= a\hspace{2pt}$(ただし$\displaystyle \lim_{x \rightarrow - \infty} x^2e^x = 0$)

【不等式への応用】
　次の不等式を証明せよ

問題32 : $\displaystyle\hspace{1pt}x > \log (x+1) \hspace{3pt}\left(\hspace{1pt} x > 0 \right)$

問題33 : $\displaystyle\hspace{1pt}\sqrt{x} > \log x \hspace{5pt}\left(\hspace{1pt} x > 0 \right)$

【微分の計算】
　次の関数を微分せよ

問題1 : $\displaystyle \hspace{3pt}y=x^3(x-1)^4(x-2)^5$

問題2 : $\displaystyle \hspace{3pt}y=\sqrt{x + \sqrt{x}}$

問題3 : $\displaystyle \hspace{3pt}y=\log \sqrt{\frac{\cos x}{\sin x + 1}}$

問題4 : $\displaystyle \hspace{3pt}y=\log_x 3$

問題5 : $\displaystyle \hspace{3pt}y=x^{\frac{1}{x}}\hspace{8pt}(x>0)$

問題6 : $\displaystyle \hspace{3pt}y=(\sin x)^{\cos x}\hspace{4pt}(0 < x < \pi)$

問題7 : $\displaystyle \hspace{3pt}y=\frac{1}{x^{x \log x}}\hspace{6pt}(x > 0)$

　次の方程式において$\displaystyle\hspace{1pt}\frac{dy}{dx}\hspace{1pt}$を求めよ

問題8 : $\displaystyle \hspace{3pt}x^2 -xy -y^2 =1$

問題9 : $\displaystyle \hspace{3pt}x^4 + y^4 =xy$

問題10 : $\displaystyle \hspace{3pt}\sin x+ \cos y=1$

　$n\hspace{1pt}$を自然数とするとき以下の式が成り立つことを数学的帰納法から証明せよ

問題11 :$\displaystyle\hspace{1pt}\frac{d^{n}}{dx^{n}} \sin x = \sin \left( x + \frac{n}{2}\pi \right)$

問題12 :$\displaystyle \hspace{1pt}\frac{d^{n}}{dx^{n}} \cos x = \cos \left( x + \frac{n}{2}\pi \right)$

問題13 :$\displaystyle \hspace{1pt}\frac{d^{n}}{dx^{n}} \log x = (-1)^{n-1}\frac{(n-1)!}{x^n}$

【関数のグラフ】
　次の関数のグラフの概形をかけ

問題14 : $\hspace{3pt} \sqrt[3]{x^2} + \sqrt[3]{y^2} = \sqrt[3]{a^2}\hspace{4pt}$$\hspace{1pt}(a > 0)\hspace{1pt}$

問題15 : $\hspace{3pt} y^2=x^2 (4-x^2)$

【最大値・最小値】
　次の関数の最大値・最小値を求めよ
問題16 : $\hspace{1pt}y=e^{-x} \sin x \hspace{3pt}(0 \leqq x \leqq 2\pi)$

問題17 : 半径$\hspace{1pt}r\hspace{2pt}$の円に内接する長方形のうち面積が最大のものを求めよ。また、そのときの各辺の長さを求めよ

【方程式への応用】
　次の方程式の実数解の個数を求めよ

問題18 : $\hspace{3pt} 2\log x - \log 2 = ax\hspace{4pt}$(ただし、$\displaystyle \lim_{x \rightarrow \infty} \frac{\log x}{x} = 0$)

問題19 : $\hspace{3pt} x^2 +x -5 = a e^x\hspace{4pt}$(ただし、$\displaystyle \lim_{x \rightarrow \infty} \frac{x^n}{e^x} = 0$)

【不等式への応用】
　次の不等式を証明せよ

問題20 : $\displaystyle\hspace{1pt}\cos x > 1 -\frac{x^2}{2} \hspace{3pt}\left(\hspace{1pt} x > 0 \right)$

問題21 : $\displaystyle\hspace{1pt}e^x > 1 + x + \frac{x^2}{2}\hspace{3pt}\left(\hspace{1pt} x > 0 \right)$

【導関数の定義】

問題1 : 次の関数の導関数を、定義に従って求めよ
　　$\displaystyle \hspace{3pt} y=x^n \hspace{5pt}$(ただし$\hspace{1pt}n\hspace{1pt}$は自然数)

問題2 : $\hspace{1pt}n\hspace{1pt}$を自然数、$a\hspace{1pt}$と$\hspace{1pt}b\hspace{1pt}$は実数の定数(ただし $a \neq 0\hspace{1pt}$)とするとき、次の関数の第$\hspace{1pt}n\hspace{1pt}$次導関数を求めよ。
　　$\displaystyle \hspace{3pt} y=\frac{1}{ax+b}$

【最大値・最小値】

問題3 : 次の関数の最大値を求めよ
　　$\displaystyle y= \frac{\sin x \cos x}{a \cos x + \sin x }\hspace{3pt}(0 < x < \frac{\pi}{2},\hspace{2pt}a > 0)$

問題4 : 次の関数の最小値を求めよ
　　$\displaystyle f(x,y) = x \log x + y \log y \hspace{3pt}$ $(x+y = 1 , x > 0 , y > 0)$

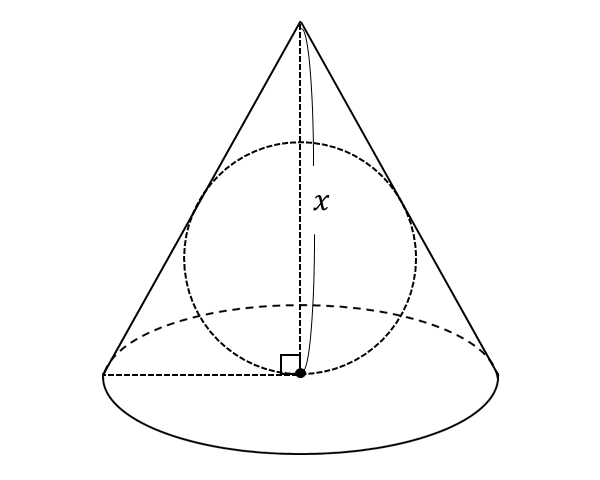
問題5 : 円錐に半径$\hspace{1pt}1\hspace{1pt}$の球が内接しているとき、円錐の表面積の最小値を求めよ

【関数のグラフ】

問題6 : (1) 曲線$\hspace{1pt}C : \sqrt{x} + \sqrt{y} = \sqrt{a}\hspace{1pt}$$\hspace{1pt}(a > 0)\hspace{1pt}$の概形をかけ

　　 　 (2) 曲線$\hspace{1pt}C\hspace{1pt}$上の任意の点における接線が$\hspace{1pt}x\hspace{1pt}$軸,$\hspace{1pt}y\hspace{1pt}$軸と交わる点をそれぞれ$\hspace{1pt}A,B\hspace{1pt}$とするとき、原点$\hspace{1pt}O\hspace{1pt}$との距離の和$\hspace{1pt}OA + OB\hspace{1pt}$が一定となることを証明せよ

【総合問題】

問題7 : (1) 次の不等式を証明せよ
　　 　　$\sqrt{x} \geqq \log x \hspace{5pt}\left(\hspace{1pt} x \geqq 1 \right)$

　　 　 (2) (1)の結果から以下の極限値を求めよ
　　 　　$\displaystyle \lim_{ x \rightarrow \infty} \frac{\log x}{x}$

　　 　 (3) $\displaystyle y = \frac{\log x}{x}\hspace{1pt}$のグラフをかけ

　　 　 (4) (3)の結果から、$e^\pi\hspace{1pt}$と$\hspace{1pt}\pi^e\hspace{1pt}$の大小関係を調べよ