三次関数が極値を持たないための条件
◆第問目!
関数\(\hspace{1pt}f(x)\hspace{1pt}\)の極値では、\(f'(x)=0\hspace{1pt}\)を満たす解\(\hspace{1pt}x\hspace{1pt}\)の前後で\(f'(x)\hspace{1pt}\)の符号の正負が変化します。
よって『関数\(\hspace{1pt}f(x)\hspace{1pt}\)が極値を持たないための条件』とは、\(f'(x)=0\hspace{1pt}\)を満たす解\(\hspace{1pt}x\hspace{1pt}\)の前後で\(f'(x)\hspace{1pt}\)の符号が変化しないことになります。
【答え】
\(\displaystyle \hspace{1pt}b \leqq -\frac{a^2}{3}\hspace{1pt}\)
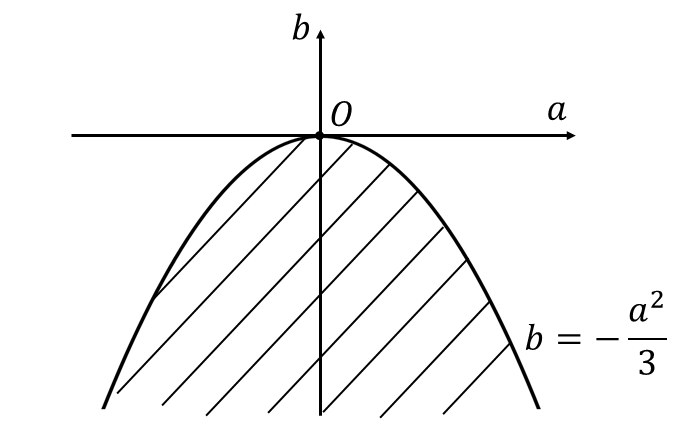
極値をもたないときの\(\hspace{1pt}(a,b)\hspace{1pt}\)の領域は以下の斜線部(ただし、境界線は含む)
【解答のポイント】
関数\(\hspace{1pt}f(x)\hspace{1pt}\)の極値では、\(f'(x)=0\hspace{1pt}\)を満たす解\(\hspace{1pt}x\hspace{1pt}\)の前後で\(f'(x)\hspace{1pt}\)の符号の正負が変化します。
よって『関数\(\hspace{1pt}f(x)\hspace{1pt}\)が極値を持たないための条件』とは、\(f'(x)=0\hspace{1pt}\)を満たす解\(\hspace{1pt}x\hspace{1pt}\)の前後で\(f'(x)\hspace{1pt}\)の符号が変化しないということになります。
\(f'(x)=0\hspace{1pt}\)は二次方程式となるため、判別式を利用して条件を求めます。
【解答】
\(f(x)=x^3 + ax^2 - bx +3\hspace{1pt}\)とすると
$${f'(x) = 3x^2 +2ax-b}$$
となります。
関数\(\hspace{1pt}f(x)\hspace{1pt}\)が極値を持たないための条件は、\(f'(x)=0\hspace{1pt}\)を満たす解\(\hspace{1pt}x\hspace{1pt}\)の前後で\(f'(x)\hspace{1pt}\)の符号が変化しないことになります。
つまり、二次方程式\(\hspace{1pt}3x^2 +2ax-b=0\hspace{1pt}\)が重解を持つか、解を持たないときに極値を持たないことから、二次方程式の判別式\(\hspace{1pt}D\hspace{1pt}\)に対して $${D \leqq 0}$$ が求める条件となります。
したがって $${a^2 +3b \leqq 0}$$ すなわち $${b \leqq -\frac{a^2}{3}}$$ となります。
また、極値をもたないときの\(\hspace{1pt}(a,b)\hspace{1pt}\)の領域を図示すると、以下の斜線部(ただし、境界線は含む)となります。
