三角関数を含む分数関数の最大最小

【解答のポイント】
最大値・最小値を求める問題は、定義域の両端や極大値・極小値の値を増減表に整理して求めます。

本問は、最大値をとる\(\hspace{1pt}x\hspace{1pt}\)の値を具体的に求めることができませんが、三角関数の定義を利用することで最大値を求めることができます。

【解答】
\(\displaystyle {f(x)= \frac{\sin x \cos x}{a \cos x + \sin x }}\) とすると

となります。

次に \({f'(x)=0}\) を満たす\(\hspace{1pt}x\hspace{1pt}\)を求めると $$\begin{aligned} \hspace{10pt} a \cos^3 x -\sin^3 x & = 0\hspace{10pt}\\[0.5em] \tan^3 x & = a\hspace{10pt}\\[0.5em] \tan x & = \sqrt[3]{a}\hspace{10pt}\\[0.5em] \end{aligned}$$

このとき、\(a > 0\hspace{1pt}\)すなわち\(\hspace{1pt} \sqrt[3]{a} > 0\hspace{1pt}\)であることから\(\hspace{1pt}x\hspace{1pt}\)は $$0 < x < \frac{\pi}{2}$$ の範囲に一つの解を持ちます。

\({f'(x)=0}\) を満たす\(\hspace{1pt}x\hspace{1pt}\)を\(\hspace{1pt}x = \alpha\hspace{1pt}\)とおくと、角度\(\hspace{1pt} \alpha\hspace{1pt}\)を持つ直角三角形の三辺は以下の図のようになります。

よって、角度\(\hspace{1pt}\alpha\hspace{1pt}\)に対して $$\begin{aligned} \hspace{10pt} \sin \alpha & = \frac{\sqrt[3]{a}}{\sqrt{1+\sqrt[3]{a^2}}}\hspace{10pt}\\[0.5em] \cos \alpha & = \frac{1}{\sqrt{1+\sqrt[3]{a^2}}}\hspace{10pt}\\[0.5em] \end{aligned}$$ が成り立ちます。

関数\(\hspace{1pt}f(x)\hspace{1pt}\)の増減表を書くと以下のようになります。

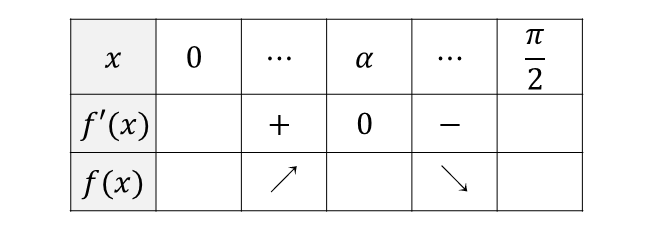
上記の増減表から最大値は $$\begin{aligned} \hspace{10pt} f(\alpha) & = \frac{\sin \alpha \cos \alpha}{a \cos \alpha + \sin \alpha }\hspace{10pt}\\[1.2em] & = \frac{\frac{\sqrt[3]{a}}{\sqrt{1+\sqrt[3]{a^2}}} \cdot \frac{1}{\sqrt{1+\sqrt[3]{a^2}}}}{a \frac{1}{\sqrt{1+\sqrt[3]{a^2}}} + \frac{\sqrt[3]{a}}{\sqrt{1+\sqrt[3]{a^2}}} }\hspace{10pt}\\[1.7em] & = \frac{\sqrt[3]{a}}{\sqrt{1+\sqrt[3]{a^2}} (a + \sqrt[3]{a}) }\hspace{10pt}\\[1em] & = \frac{1}{\sqrt{1+\sqrt[3]{a^2}} (1 + \sqrt[3]{a^2}) }\hspace{10pt}\\[1em] & = \frac{1}{ (1 + \sqrt[3]{a^2})^{\frac{3}{2}} }\hspace{10pt}\\[1em] \end{aligned}$$

となります。