三次関数のグラフ

【解答】

\(\displaystyle {f(x)=2x^3-6x}\) とすると $${f'(x)=6x^2-6}$$ となります。

\({f'(x)=0}\) を解くと $$\begin{aligned} 6x^2-6 & =0\\[0.5em] 6(x^2-1) & =0\\[0.5em] 6(x-1)(x+1) & =0\\[0.5em] \end{aligned}$$ よって、\(x = \pm 1\hspace{1pt}\)となります。

ここで、\({x=\pm 1}\) の前後における \(\displaystyle{f'(x)}\) の符号の変化を調べます。

\({f'(x)=6(x-1)(x+1)}\) より
　　\({x < -1}\)　　 のとき \({f'(x)>0}\)
　　\({-1 < x < 1\hspace{2pt}}\) のとき \({f'(x)< 0}\)
　　\({ x > 1}\) 　　　のとき \({f'(x) > 0}\)
となります。

よって、関数\(\displaystyle {f(x)}\) は\({x=-1}\) で極大値、\({x=1}\) で極小値をとります。

以上から、増減表を作ると 以下のようになります。

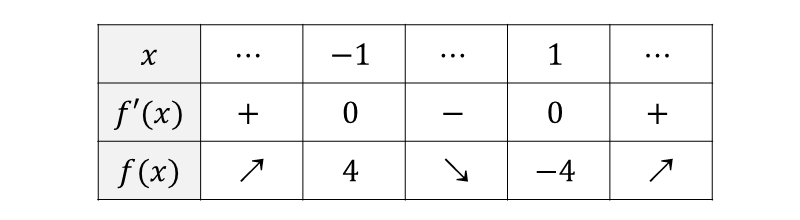
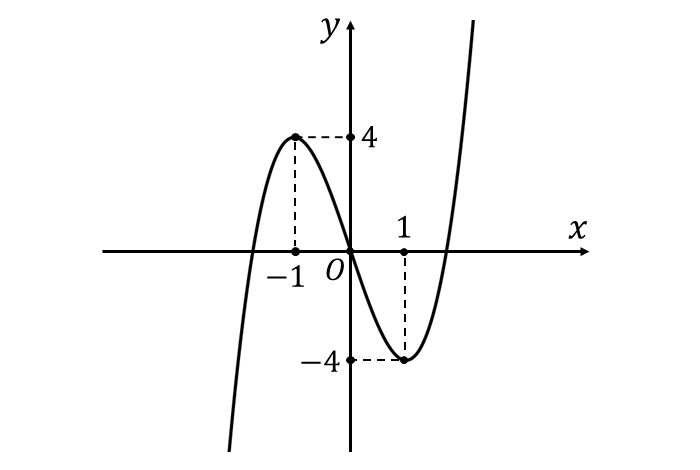
この増減表からグラフを描くと、以下のようになります。