定数分離できない三次方程式の実数解の個数

【解答のポイント】

文字の定数\(\hspace{1pt}a\hspace{1pt}\)を含む場合は定数分離による解法が定石ですが、本問は定数項以外にも文字\(\hspace{1pt}a\hspace{1pt}\)が含まれているため、定数項を移項する定数分離ができません。

(数Ⅲの分数関数の微分を用いると、\(\hspace{1pt}\frac{x^3}{3x^2-4}=a\hspace{1pt}\)と変形することで、定数分離から解の個数を求めることもできます。)

そこで、関数\(\hspace{1pt}y=f(x)\hspace{1pt}\)が\(\hspace{1pt}x=\alpha,\beta\hspace{1pt}\)に極値をもつときに、極値の積\(\hspace{1pt}f(\alpha)f(\beta)\hspace{1pt}\)の符号が実数解の個数に対応するという性質を利用して解きます。

\(f(\alpha)f(\beta) < 0\hspace{1pt}\)のときは、以下のように\(\hspace{1pt}x\hspace{1pt}\)軸と\(\hspace{1pt}3\hspace{1pt}\)個の共有点を持つため、方程式\(\hspace{1pt}f(x)=0\hspace{1pt}\)は\(\hspace{1pt}3\hspace{1pt}\)個の実数解を持ちます。
(グラフは\(\hspace{1pt}x^3\hspace{1pt}\)の係数が正ですが、係数が負の場合も同様になります。)

\(f(\alpha)f(\beta) = 0\hspace{1pt}\)のときは、以下のように\(\hspace{1pt}x\hspace{1pt}\)軸と\(\hspace{1pt}2\hspace{1pt}\)個の共有点を持つため、方程式\(\hspace{1pt}f(x)=0\hspace{1pt}\)は\(\hspace{1pt}2\hspace{1pt}\)個の実数解を持ちます。

\(f(\alpha)f(\beta) > 0\hspace{1pt}\)のときは、以下のように\(\hspace{1pt}x\hspace{1pt}\)軸と\(\hspace{1pt}1\hspace{1pt}\)個の共有点を持つため、方程式\(\hspace{1pt}f(x)=0\hspace{1pt}\)は\(\hspace{1pt}1\hspace{1pt}\)個の実数解を持ちます。

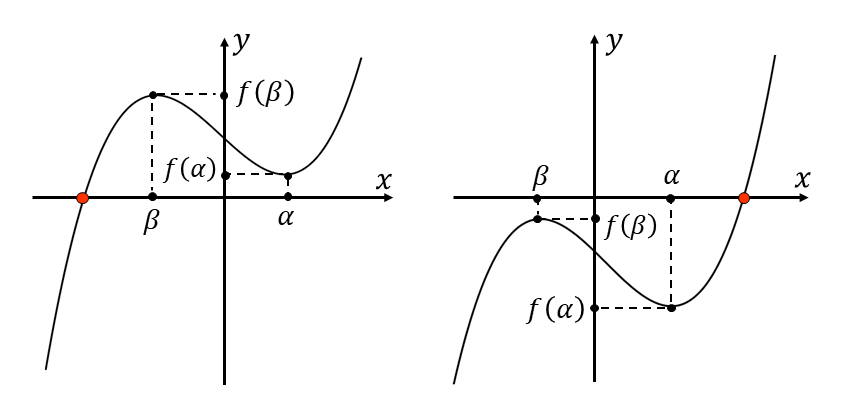
上記の性質を整理すると、方程式\(\hspace{1pt}f(x)=0\hspace{1pt}\)の実数解の個数は
　\(\hspace{1pt}f(\alpha)f(\beta) < 0\hspace{1pt}\)のときに\(\hspace{1pt}3\hspace{1pt}\)個
　\(\hspace{1pt}f(\alpha)f(\beta) = 0\hspace{1pt}\)のときに\(\hspace{1pt}2\hspace{1pt}\)個
　\(\hspace{1pt}f(\alpha)f(\beta) > 0\hspace{1pt}\)のときに\(\hspace{1pt}1\hspace{1pt}\)個
となります。

【解答】
\(f(x)=x^3-3ax^2 +4a\hspace{1pt}\)とすると $${f'(x) = 3x^2 -6ax }$$ となります。

\({f'(x)=0}\) を解くと $$\begin{aligned} 3x^2 -6ax & =0\\[0.5em] 3x(x-2a) & =0\\[0.5em] \end{aligned}$$ よって\(\displaystyle\hspace{3pt}x = 0 ,2a\hspace{1pt}\)となります。

ここで、\(\displaystyle x =0,2a\hspace{1pt}\)の前後における \(\displaystyle{f'(x)}\) の符号の変化を調べます。

\({f'(x)=3x(x-2a) }\) より
　　\({\displaystyle x < 0}\)　　　 のとき \({f'(x) > 0}\)
　　\({\displaystyle 0 < x < 2a\hspace{2pt}}\)　のとき \({f'(x) < 0}\)
　　\({ x > 2a}\) 　　　のとき \({f'(x) > 0}\)
となります。

よって、関数\(\displaystyle {f(x)}\) は \({\displaystyle x = 0}\) で極大値\(\hspace{1pt}f(0)=4a\hspace{1pt}\)、\({x=2a}\) で極小値\(\hspace{1pt}f(2a)=4a(1-a^2)\hspace{1pt}\)をとります。

ここで、極値の積を考えると $$\begin{aligned} & f(0)f(2a) \\[0.5em] & =4a \cdot 4a (1-a^2)\\[0.5em] & =16a^2 (1-a^2)\\[0.5em] \end{aligned}$$ \(a > 0\hspace{1pt}\)であることから、極値の積の符号は\(\hspace{1pt}(1-a^2)\hspace{1pt}\)により決まります。

よって、実数解の数は定数\(\hspace{1pt}a\hspace{1pt}\)によって以下のようになります。

\(\hspace{1pt}1-a^2< 0 \hspace{1pt}\)すなわち\(\hspace{1pt} a > 1\hspace{1pt}\)のとき、\(f(0)f(2a) < 0\hspace{1pt}\)となることから、実数解の個数は\(\hspace{1pt}3\hspace{1pt}\)個

\(\hspace{1pt}1-a^2 = 0 \hspace{1pt}\)すなわち\(\hspace{1pt} a = 1\hspace{1pt}\)のとき、\(f(0)f(2a) = 0\hspace{1pt}\)となることから、実数解の個数は\(\hspace{1pt}2\hspace{1pt}\)個

\(\hspace{1pt}1-a^2 > 0 \hspace{1pt}\)すなわち\(\hspace{1pt} 0 < a < 1\hspace{1pt}\)のとき、\(f(0)f(2a) > 0\hspace{1pt}\)となることから、実数解の個数は\(\hspace{1pt}1\hspace{1pt}\)個

となります。