球が内接する円錐の表面積の最小値
◆第問目!
(1) 以下の図のように、円錐の高さを\(\hspace{1pt}x\hspace{1pt}\)とするとき円錐の表面積を\(\hspace{1pt}x\hspace{1pt}\)で表せ。
(2) 円錐の表面積の最小値を求めよ。
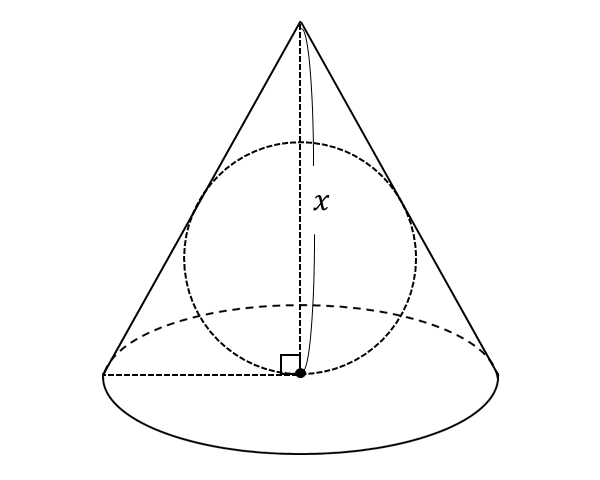
まず、円錐の底面の中心を通り、底面に垂直な平面における断面図を書きます。

円錐の表面積を求めるためには、底面の円の半径が必要であるため、まずは図の\(\hspace{1pt}BQ\hspace{1pt}\)の長さを求めることを目指します。
そこで、三角形\(\hspace{1pt}ABQ\hspace{1pt}\)と\(\hspace{1pt}APO\hspace{1pt}\)が相似であることを利用して、\(\hspace{1pt}BQ\hspace{1pt}\)の長さを求めます。
円錐を展開した扇形の中心角\(\hspace{1pt}\theta\hspace{1pt}\)(ラジアン)、半径\(\hspace{1pt}R\hspace{1pt}\)、円弧の長さ\(\hspace{1pt}L\hspace{1pt}\)の関係式 $${ R \theta = L}$$ から中心角は $${ \theta = \frac{L}{R}}$$ となります。
扇形の中心角\(\hspace{1pt}\theta\hspace{1pt}\)と半径\(\hspace{1pt}R\hspace{1pt}\)、円錐の底面の半径\(\hspace{1pt}r\hspace{1pt}\)から、円錐の表面積\(\hspace{1pt}S\) $${S = \frac{1}{2} R^2 \theta + \pi r^2}$$ から表面積を\(\hspace{1pt}x\hspace{1pt}\)で表すことができます。
問題(1)で求めた円錐の表面積を\(\hspace{1pt}x\hspace{1pt}\)で微分して増減表を作り、表面積の最小値を求めます。
【答え】
(1) \(\displaystyle \pi\frac{x^2}{x -2} \hspace{1pt}\)
(2) \(8 \pi \hspace{1pt}\)
【解答のポイント】
本問では、円錐の底面の中心を通り、底面に垂直な平面の断面を書いて、内接する球との関係を整理します。
断面の図中に相似な三角形あることから、他の辺の長さを\(\hspace{1pt}x\hspace{1pt}\)で表すことができます。
『円錐に球が内接している』という条件の問題は『断面に相似な三角形があることを利用する』ことが多いため、パターンとして覚えておくと他の問題でも役に立ちます。
【(1)の解答】
円錐の底面の中心を通り、底面に垂直な平面の断面を図にすると以下のようになります。

断面の三角形の頂点を\(\hspace{1pt}A,B,C\hspace{1pt}\)とします。
また、内接する円の中心を点\(\hspace{1pt}O\hspace{1pt}\)、点\(\hspace{1pt}O\hspace{1pt}\)から辺\(\hspace{1pt}AB\hspace{1pt}\)に垂直に引いた垂線の足を点\(\hspace{1pt}P\hspace{1pt}\)、点\(\hspace{1pt}O\hspace{1pt}\)から辺\(\hspace{1pt}BC\hspace{1pt}\)に垂直に引いた垂線の足を点\(\hspace{1pt}Q\hspace{1pt}\)とします。
線分\(\hspace{1pt}AO\hspace{1pt}\)の長さが\(\hspace{1pt}x-1\hspace{1pt}\)、線分\(\hspace{1pt}PO\hspace{1pt}\)の長さが\(\hspace{1pt}1\hspace{1pt}\)であることから、線分\(\hspace{1pt}AP\hspace{1pt}\)の長さは
$$\sqrt{(x-1)^2 - 1^2}= \sqrt{x^2 -2x}$$ となります。
このとき、\(x\hspace{1pt}\)の定義域は\(\hspace{2pt} x > 0\hspace{2pt}\)かつ\(\hspace{2pt}x^2 -2x > 0\hspace{2pt}\)であるので $${ x > 2}$$ となります。
ここで、底面の半径を\(\hspace{1pt}r\hspace{1pt}\)として相似な三角形\(\hspace{1pt}ABQ\hspace{1pt}\)と\(\hspace{1pt}APO\hspace{1pt}\)に注目すると $${r : x = 1 : \sqrt{x^2 -2x} }$$ すなわち $$\begin{aligned} x & = r\sqrt{x^2 -2x} \\[0.7em] r & = \frac{x}{\sqrt{x^2 -2x}} \\[0.7em] & = \sqrt{\frac{x}{x -2} }\\[0.5em] \end{aligned}$$ となります。
ここで、円錐を展開した扇形の中心角を\(\hspace{1pt}\theta\hspace{1pt}\)(ラジアン)とすると、半径\(\hspace{1pt}\sqrt{r^2 + x^2}\hspace{1pt}\)、円弧の長さは円錐の底面の円周と一致することから\(\hspace{1pt}2 \pi r\hspace{1pt}\)であるため $$\begin{aligned} \sqrt{r^2 + x^2} \times \theta & = 2 \pi r \\[0.7em] \theta & = \frac{ 2 \pi r }{\sqrt{r^2 + x^2}} \\[0.7em] \end{aligned}$$ したがって、円錐の表面積を\(\hspace{1pt}f(x)\hspace{1pt}\)とすると
となります。
\(\displaystyle r = \sqrt{\frac{x}{x -2} }\hspace{1pt}\)であることから
\(\displaystyle x > 2 \hspace{1pt}\)であることから、円錐の表面積は
となります。
【(2)の解答】
関数\(\hspace{1pt}f(x)\hspace{1pt}\)の一次導関数を求めると
となります。
\(\displaystyle x > 2 \hspace{1pt}\)において\({\hspace{1pt} f'(x)=0}\) を満たす\(\hspace{1pt}x\hspace{1pt}\)を求めると $${ \pi\frac{x(x - 4)}{(x -2)^2} = 0}$$ から $${x = 4 }$$ となります。
ここで、\(\displaystyle x=4 \hspace{1pt}\)の前後における \(\displaystyle{f'(x)}\) の符号の変化を調べます。
\(\displaystyle f'(x)=\pi\frac{x(x - 4)}{(x -2)^2} \) より
\({\displaystyle 2 < x < 4}\) のとき \({f'(x) < 0}\)
\({ x > 4 \hspace{2pt}}\) のとき \({f'(x) > 0}\)
となります。
よって、関数\(\displaystyle {f(x)}\) は \({\displaystyle x=4 }\) で極小値をとります。
関数\(\hspace{1pt}f(x)\hspace{1pt}\)の増減表を書くと以下のようになります。
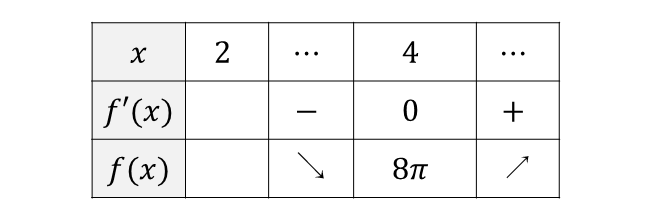
上記の増減表から、円錐に半径\(\hspace{1pt}1\hspace{1pt}\)の球が内接しているときの円錐の表面積の最小値は\(\hspace{1pt}8 \pi\hspace{1pt}\)となります。
【関連するページ】
・増減表の作り方