三辺の和と表面積が与えられた直方体の体積

【解答のポイント】
本問では縦、横、高さの三辺が未知数であるため、三辺の長さをそれぞれ\(\hspace{1pt}(X,Y,Z)\hspace{1pt}\)とおきます。

与えられた条件から、体積を\(\hspace{1pt}V\hspace{1pt}\)とすると $$ \begin{aligned} X+Y+Z & = 5\\[0.7em] 2(XY+YZ+XZ) & = 16\\[0.7em] XYZ & = V\\[0.7em] \end{aligned} $$ とおくことができます。

ここで、三次方程式\(\hspace{1pt}x^3 + ax^2 +bx +c = 0\hspace{1pt}\)の解が\(\hspace{1pt}\alpha,\beta,\gamma\hspace{1pt}\)であるとき、解と係数の関係から $$ \begin{aligned} \alpha + \beta + \gamma & = -a\\[1em] \alpha\beta + \beta\gamma + \gamma\alpha & = b\\[1em] \alpha \beta \gamma & = -c\\[1em] \end{aligned} $$ であることから\(\hspace{1pt}X,Y,Z\hspace{1pt}\)は三次方程式 $${t^3 -5 t^2 + 8t - V = 0}$$ の解となります。

【解答】
縦, 横, 高さの三辺をそれぞれ\(\hspace{1pt}(X,Y,Z)\hspace{1pt}\)とおきます。

三辺の和が\(\hspace{1pt}5\hspace{1pt}\)であることから $${X+Y+Z = 5}$$ となります。

また、表面積が\(\hspace{1pt}16\hspace{1pt}\)であることから $${2(XY+YZ+XZ) = 16}$$ となります。

また、体積を\(\hspace{1pt}V\hspace{1pt}\)とすると $${XYZ = V}$$ となります。

ここで、解と係数の関係から\(\hspace{1pt}X,Y,Z\hspace{1pt}\)は三次方程式 $${t^3 -5 t^2 + 8t - V = 0 \cdots (1)}$$ の解となります。

ここで、\(\hspace{1pt}V\hspace{1pt}\)を右辺に移項します。 $${t^3 -5 t^2 + 8t = V}$$ 次に、左辺と右辺をそれぞれ $$\begin{aligned} y & =t^3 -5 t^2 + 8t\\[0.5em] y & =V\\[0.5em] \end{aligned}$$ とします。このとき、上記の2つの関数の交点の個数が、方程式(1)の実数解の個数となります。

\(f(t)=t^3 -5 t^2 + 8t\hspace{1pt}\)とすると $${f'(t) = 3t^2 -10t + 8}$$ となります。

\({f'(t)=0}\) を解くと $$\begin{aligned} 3t^2 -10t + 8& =0\\[0.5em] (3t-4)(t-2) & =0\\[0.5em] \end{aligned}$$ よって\(\displaystyle\hspace{3pt}t = \frac{4}{3},2\hspace{1pt}\)となります。

ここで、\(\displaystyle t = \frac{4}{3},2\hspace{1pt}\)の前後における \(\displaystyle{f'(t)}\) の符号の変化を調べます。

\({f'(t)=(3t-4)(t-2) }\) より
　　\({\displaystyle t < \frac{4}{3}}\)　　 のとき \({f'(t) > 0}\)
　　\({\displaystyle \frac{4}{3} < t < 2\hspace{2pt}}\) のとき \({f'(t) < 0}\)
　　\({ t > 2}\) 　　　のとき \({f'(t) > 0}\)
となります。

よって、関数\(\displaystyle {f(t)}\) は \({\displaystyle t = \frac{4}{3}}\) で極大値、\({t=2}\) で極小値をとります。

以上から、増減表を作ると 以下のようになります。

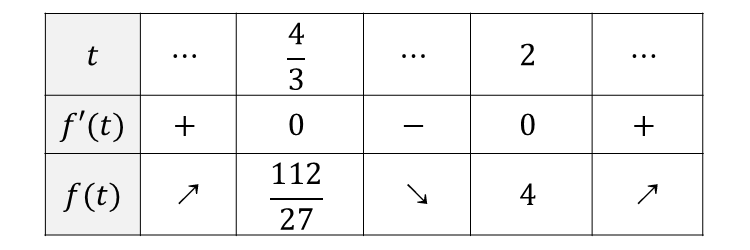
上記の増減表から、\(y=t^3 -5 t^2 + 8t\hspace{1pt}\)のグラフは以下のようになります。

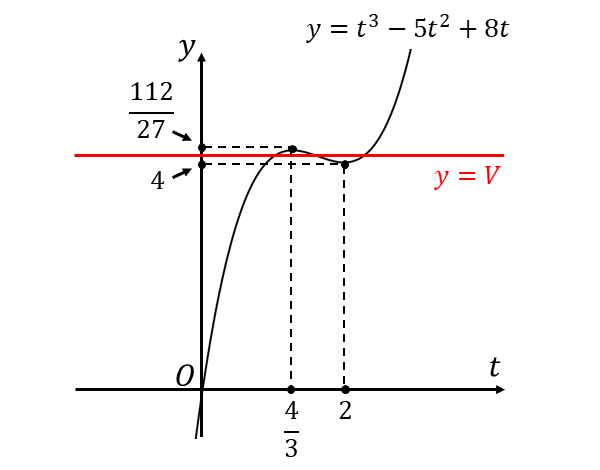
ここで、\(y=t^3 -5 t^2 + 8t\hspace{2pt}\)と\(\hspace{2pt}y=V\hspace{2pt}\)が\(\hspace{1pt}3\hspace{1pt}\)つの交点を持つとき、\(\hspace{1pt}V\hspace{1pt}\)の範囲は $${ 4 \leqq V \leqq \frac{112}{27}}$$ となります。

したがって
\(\displaystyle t = \frac{4}{3}\hspace{1pt}\)のとき最大値\(\displaystyle \hspace{1pt}\frac{112}{27}\hspace{1pt}\)
\(t = 2\hspace{1pt}\)のとき最小値\(\hspace{1pt}4\hspace{1pt}\)
となります。

最小値をとるとき\(\hspace{2pt}t = 2\hspace{2pt}\)で重解となることから、残りの一つの解は $${5-2-2 = 1}$$ すなわち、求める縦,横,高さの三辺の長さは\(\displaystyle\hspace{1pt}1 , 2, 2\hspace{1pt}\)(ただし、順不動)となります。

また、最大値となる三辺の長さを求めると
最大値をとるとき\(\hspace{2pt}t = \frac{4}{3}\hspace{2pt}\)で重解となることから、残りの一つの解は $${5-\frac{4}{3}-\frac{4}{3} = \frac{7}{3}}$$ すなわち、求める縦,横,高さの三辺の長さは\(\displaystyle\hspace{1pt}\frac{4}{3},\frac{4}{3},\frac{7}{3}\hspace{1pt}\)(ただし、順不動)となります。

以上から、
縦,横,高さの三辺の長さが\(\displaystyle\hspace{1pt}1 , 2, 2\hspace{1pt}\)(ただし、順不動)のとき最小値\(\hspace{1pt}4\hspace{1pt}\)
縦,横,高さの三辺の長さが\(\displaystyle\hspace{1pt}\frac{4}{3},\frac{4}{3},\frac{7}{3}\hspace{1pt}\)(ただし、順不動)のとき最大値\(\displaystyle\hspace{1pt}\frac{112}{27}\hspace{1pt}\)
となります。