y=logx/xの最大値と最小値

【解答】
\(\displaystyle {f(x)=\frac{\log x}{ x}}\) とすると

となります。

次に \({f'(x)=0}\) を満たす\(\hspace{1pt}x\hspace{1pt}\)を求めると

$${1 - \log x = 0}$$ すなわち $$\begin{aligned} \hspace{10pt}\log x & =1\hspace{10pt}\\[0.5em] x & = e\\[0.5em] \end{aligned}$$ となります。

ここで、\(\displaystyle x = e \hspace{1pt}\)の前後における\(\displaystyle{\hspace{1pt}f'(x)\hspace{1pt}}\)の符号を調べます。

　\({\displaystyle \frac{1}{e} < x < e}\)　　のとき \({f'(x) > 0}\)

　\({\displaystyle e < x < e^2}\) 　 のとき \({f'(x) < 0}\)

以上から、関数 \(\displaystyle {f(x)}\) は\(\displaystyle {\hspace{2pt}x=e}\) で極大値をとります。

以上から、増減表を作ると 以下のようになります。

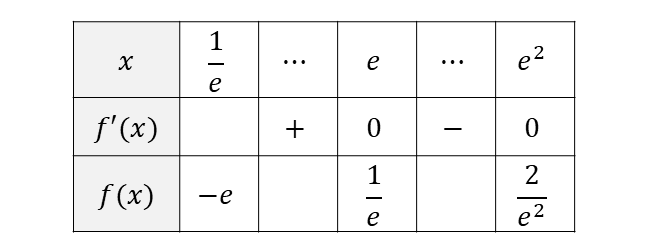
上記の増減表から問題の関数は

\({\displaystyle\hspace{1pt}x=e\hspace{1pt}}\)で最大値\(\displaystyle\hspace{1pt}\frac{1}{e}\hspace{1pt}\)

\({\displaystyle\hspace{1pt}x= \frac{1}{e}\hspace{1pt}}\)で最小値\(\displaystyle\hspace{1pt}-e\hspace{1pt}\)

をとります。