三辺の和が与えられた直方体の体積

【解答】
まず、底面の一辺の長さを変数\(\hspace{1pt}x\hspace{1pt}\)とおくと、高さは\(\hspace{2pt}12-2x\hspace{2pt}\)となります。

変数\(\hspace{1pt}x\hspace{1pt}\)の範囲は、\(\hspace{1pt}x>0\hspace{1pt}\)かつ\(\hspace{1pt}12-2x > 0\hspace{1pt}\)であることから $${ 0 < x < 6}$$ となります。

問題の直方体の体積を\(\hspace{1pt}y\hspace{1pt}\)とすると $$ \begin{aligned} y & = x^2 (12-2x)\\[1em] & = -2x^3 + 12x^2\\[1em] \end{aligned} $$ となります。

また、上式を微分すると $$y' = -6x^2 + 24x $$ となります。

\(y'=0\hspace{1pt}\)を計算すると $$\begin{aligned} -6x^2 + 24x & =0\\[0.5em] -6x(x-4) & =0\\[0.5em] \end{aligned}$$

となることから、\( 0 < x < 6\hspace{1pt}\)の範囲で解を求めると $$ x = 4 $$ となります。

ここで、\( 0 < x < 6\hspace{1pt}\)の範囲で増減表を作ると以下のようになります。

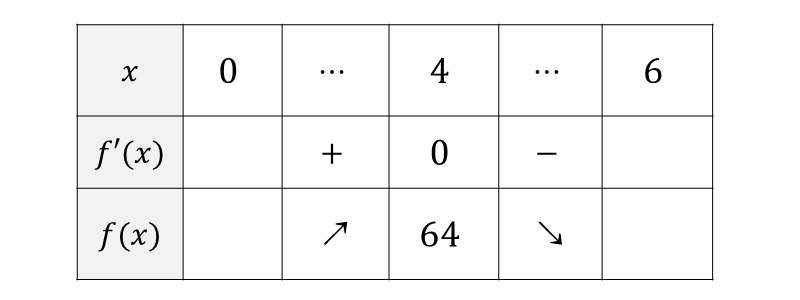
したがって、\(y=-2x^3 + 12x^2\hspace{2pt}\)は\(\displaystyle\hspace{1pt}x= 4 \hspace{1pt}\)において最大値\(\displaystyle\hspace{1pt}64\hspace{1pt}\)をとります。

以上から、問題の直方体の体積の最大値は\(\displaystyle\hspace{1pt}64\hspace{1pt}\)、そのときの直方体は三辺が\(\displaystyle\hspace{1pt}4\hspace{1pt}\)の立方体となります。