三次の三角関数の不等式を示す問題

【解答のポイント】
ある区間において\(\hspace{1pt}f(x) \geqq a\hspace{1pt}\)であることを証明するには、その区間で関数\(\hspace{1pt}f(x)\hspace{1pt}\)の最小値が\(\hspace{1pt}a\hspace{1pt}\)であることを示します。

本問では、\(\cos x =t\hspace{1pt}\)とおき、\(\hspace{1pt}t\hspace{1pt}\)に関する三次関数の最小値が\(\hspace{1pt}0\hspace{1pt}\)以上であることを示します。

【解答】
まず、不等式の左辺を\(\hspace{1pt}f(x)\hspace{1pt}\)とおいて変形すると

となります。

ここで\(\hspace{2pt}\cos x =t\hspace{1pt}\)とすると $${f(t) = 4 t^3 - t^2 -2 t +3 }$$ となります。

このとき、\( 0 \leqq x \leqq 2\pi\hspace{2pt}\)であることから、\(\hspace{1pt}t\hspace{1pt}\)の範囲は $${ -1 \leqq t \leqq 1}$$ となります。

\(t\hspace{1pt}\)について微分すると $${f'(t) = 12 t^2 -2t -2 }$$ となります。

\({f'(t)=0}\) を解くと $$\begin{aligned} 12 t^2 -2t -2 & =0\\[0.5em] 2 (6 t^2 -t -1) & =0\\[0.5em] 2 (2t -1)(3t+1) & =0\\[0.5em] \end{aligned}$$ よって\(\displaystyle\hspace{3pt}t = -\frac{1}{3} , \frac{1}{2}\hspace{1pt}\)となります。

ここで、\(\displaystyle t = -\frac{1}{3} , \frac{1}{2}\hspace{1pt}\)の前後における \(\displaystyle{f'(t)}\) の符号の変化を調べます。

\({\displaystyle f'(t)=2 (2t -1)(3t+1) }\) より
　\({\displaystyle t < -\frac{1}{3}}\)　　　のとき \({f'(t) > 0}\)
　\({\displaystyle -\frac{1}{3} < t < \frac{1}{2} \hspace{2pt}}\)　のとき \({f'(t) < 0}\)
　\({\displaystyle t > \frac{1}{2}}\) 　　　　のとき \({f'(t) > 0}\)
となります。

よって、関数\(\displaystyle {f(t)}\) は \({\displaystyle t = \frac{1}{2}}\) で極小値、\({\displaystyle t= -\frac{1}{3}}\) で極大値をとります。

以上から、増減表を作ると 以下のようになります。

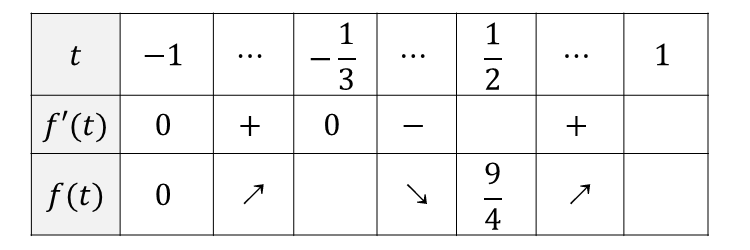
上記の増減表から、\(\hspace{1pt}-1 \leqq t \leqq 1\hspace{1pt}\)における関数\(\displaystyle \hspace{1pt} f(t)= 4 t^3 - t^2 -2 t +3\hspace{1pt}\) は
　\(\displaystyle t = -1\hspace{1pt}\)で最小値\(\displaystyle\hspace{1pt}0\hspace{1pt}\)
となります。

したがって、問題の\(\hspace{3pt}0 \leqq x \leqq 2\pi\hspace{2pt}\hspace{1pt}\)における不等式

の左辺が\(\hspace{1pt}x = \pi\hspace{1pt}\)において最小値\(\hspace{1pt}0\hspace{1pt}\)を取ることから、不等式は成り立ちます。