条件付きの二変数の関数の最小値

【解答のポイント】
本問は二変数\(\hspace{1pt}(x,y)\hspace{1pt}\)を含む関数の最小値を求める問題です。

与えられた条件式\(\hspace{1pt}x+y = 1\hspace{1pt}\)から変数の数を減らし、\(x\hspace{1pt}\)のみの関数に変形して最小値を求めます。

変数を置き換えるときに、定義域の確認を忘れないように注意が必要です。

【解答】
条件式\(\hspace{1pt}x + y = 1\hspace{1pt}\)から $$ { y = 1 -x}$$ となります。

このとき、\(y > 0\hspace{1pt}\)から\(\hspace{1pt}x\hspace{1pt}\)の定義域は\(\hspace{1pt} 0 < x < 1\hspace{1pt}\)となります。

問題の関数を\(\hspace{1pt}x\hspace{1pt}\)で表すと $${f(x) = x \log x + (1-x) \log (1-x)}$$ となります。

一次導関数を求めると

となります。

\({f'(x)=0}\) を満たす\(\hspace{1pt}x\hspace{1pt}\)を求めると $${ \log \frac{x}{1-x} = 0}$$ すなわち $${ \frac{x}{1-x} = 1}$$ $${x = \frac{1}{2}}$$ となります。

ここで、\(\displaystyle\frac{1}{2}\hspace{1pt}\)の前後における \(\displaystyle{f'(x)}\) の符号の変化を調べます。

\(\displaystyle f'(x)=\log \frac{x}{1-x} \) より
　\({\displaystyle 0 < x < \frac{1}{2}}\)　 のとき \({f'(x) < 0}\)
　\({ \displaystyle \frac{1}{2} < x < 1\hspace{2pt}}\)　のとき \({f'(x) > 0}\)
となります。

よって、関数\(\displaystyle {f(x)}\) は \({\displaystyle x=\frac{1}{2}}\) で極小値をとります。

関数\(\hspace{1pt}f(x)\hspace{1pt}\)の増減表を書くと以下のようになります。

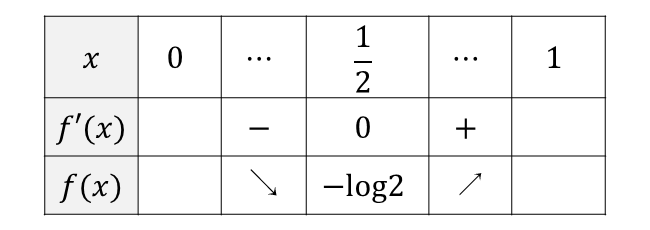
上記の増減表から、\(\displaystyle x = \frac{1}{2}\hspace{1pt}\)のとき関数\(\hspace{1pt}f(x)\hspace{1pt}\)は最小値\(\hspace{1pt} -\log 2\hspace{1pt}\)となります。

条件式\(\hspace{1pt}x+y=1\hspace{1pt}\)から \(\displaystyle x = \frac{1}{2} , y = \frac{1}{2}\hspace{1pt}\)のとき関数\(\hspace{1pt}f(x,y)\hspace{1pt}\)は最小値\(\hspace{1pt} -\log 2\hspace{1pt}\)となります。