リサジュー曲線の作図

【解答のポイント】
陰関数のグラフを描く問題は、まず『対称性』と『定義域』を調べることから始めます。

陰関数$\hspace{1pt}f(x,y)=0\hspace{1pt}$に対して

　・$f(-x,y) = f(x,y)\hspace{1pt}$であれば$\hspace{1pt}y\hspace{1pt}$軸対称

　・$f(x,-y) = f(x,y)\hspace{1pt}$であれば$\hspace{1pt}x\hspace{1pt}$軸対称

となります。

対称性がある場合、グラフの形状を調べる象限を限定することで計算が簡単になります。

【解答】
まず、問題の関数の対称性について調べると $${(-x)^2} = x^2$$ $${ (-y)^2 = y^2}$$ であることから、$x\hspace{1pt}$軸と$\hspace{1pt}y\hspace{1pt}$軸に関して対称であることが分かります。

そのため、$x \geqq 0 , y \geqq 0\hspace{1pt}$の範囲で調べます。

また、問題の関数を変形した$\hspace{1pt} y = x \sqrt{4-x^2} \hspace{3pt}$から $$\begin{aligned} \hspace{10pt}4-x^2 & \geqq 0\hspace{10pt}\\[0.5em] x^2 & \leqq 4 \hspace{10pt}\\[0.5em] \end{aligned}$$ よって、$x\hspace{1pt}$の定義域は $${ 0 \leqq x \leqq 2}$$ となります。

$\displaystyle {f(x)= x (4-x^2)^\frac{1}{2}}$ とすると

となります。

また、第二次導関数を求めると

となります。

$f'(x) = 0\hspace{1pt}$を解くと $${\frac{-2(x + \sqrt{2})(x - \sqrt{2})}{(4-x^2)^\frac{1}{2} } = 0}$$ から$\hspace{1pt}x = \sqrt{2}\hspace{1pt}$となります。

ここで、$x =\sqrt{2}\hspace{1pt}$の前後における $\displaystyle{f'(x)}$ の符号の変化を調べます。

$\displaystyle f'(x)=\frac{-2(x + \sqrt{2})(x - \sqrt{2})}{(4-x^2)^\frac{1}{2} }$ より
　${0 < x < \sqrt{2}}$　　　 のとき ${f'(x) > 0}$
　${ \sqrt{2} < x < 2\hspace{2pt}}$　のとき ${f'(x) < 0}$
となります。

よって、関数$\displaystyle {f(x)}$ は ${x=\sqrt{2}}$ で極大値をとります。

また、第二次導関数$\hspace{1pt}f''(x)\hspace{1pt}$は$\hspace{3pt} 0 < x < 2\hspace{3pt}$において$\hspace{1pt}f''(x) < 0\hspace{1pt}$となります。

以上から、増減表を作ると 以下のようになります。

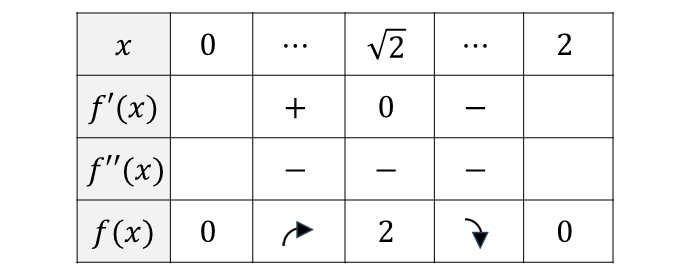
ここで、一次導関数の極限値を調べると $$\begin{aligned} \lim_{x \rightarrow +0} f'(x) & = 2\hspace{10pt}\\[1.2em] \hspace{10pt}\lim_{x \rightarrow 2-0} f'(x) & = - \infty\hspace{10pt}\\[1.2em] \end{aligned}$$ となります。

すなわち、$x = 0\hspace{1pt}$では曲線の接線の傾きが$\hspace{1pt}2\hspace{1pt}$、$x = 2\hspace{1pt}$では曲線の接線の傾きが$\hspace{1pt}y\hspace{1pt}$軸に平行となることが分かります。

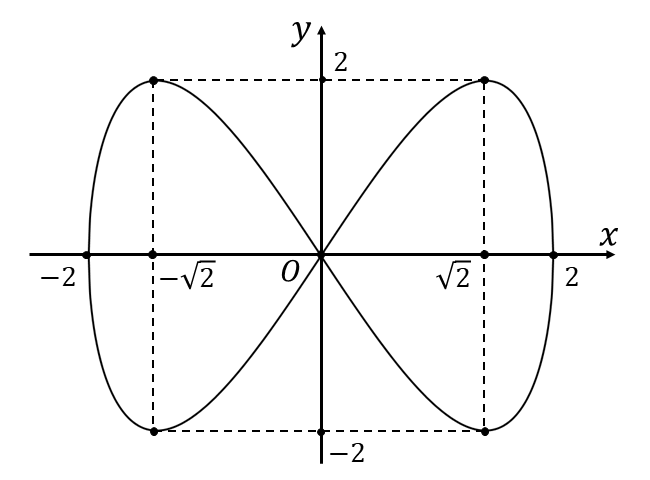
以上から、問題の関数のグラフは以下のようになります。