logx/xのグラフとe^πとπ^eの大小関係
◆第問目!
ある区間において\(\hspace{1pt}f(x) > a\hspace{1pt}\)であることを証明するには、その区間で関数\(\hspace{1pt}f(x)\hspace{1pt}\)の最小値が\(\hspace{1pt}a\hspace{1pt}\)より大きいことを示します。
本問は、両辺に変数\(\hspace{1pt}x\hspace{1pt}\)があるため、移項して\(\hspace{1pt}f(x) > a\hspace{1pt}\)の式に変形して証明します。
はさみうちの原理から、ある関数\(\hspace{1pt}f(x),g(x),h(x)\hspace{1pt}\)について $${f(x) \leqq h(x) \leqq g(x)}$$ が成り立つ場合 $$ \lim_{x \rightarrow \infty} f(x) = \alpha , \lim_{x \rightarrow \infty} g(x) = \alpha $$ であるとき $${\lim_{x \rightarrow \infty} h(x) = \alpha }$$ となります。
【(1)の解答】
\(\sqrt{x} \geqq \log x\hspace{1pt}\)を移項した $${\sqrt{x} - \log x \geqq 0}$$ を証明することで、不等式\(\hspace{1pt} \sqrt{x} \geqq \log x\hspace{1pt}\)を証明します。
\(f(x)=\sqrt{x} - \log x\hspace{1pt}\)とすると $$\begin{aligned} f'(x) & = \frac{1}{2\sqrt{x}} - \frac{1}{x}\\[0.5em] & = \frac{\sqrt{x} - 2}{2x}\\[0.5em] \end{aligned}$$ となります。
\({f'(x)=0}\) を解くと $$\begin{aligned} \sqrt{x} - 2 & =0\\[0.5em] \sqrt{x} & =2\\[0.5em] x & =4\\[0.5em] \end{aligned}$$ となります。
関数\(\hspace{1pt}f(x)\hspace{1pt}\)の増減表を作ると 以下のようになります。
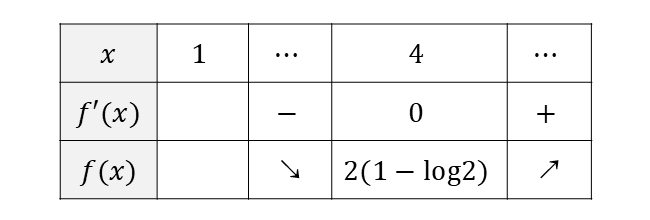
増減表から、関数\(\displaystyle {f(x)}\) は \({x \geqq 1}\) において\(\hspace{1pt}x=4\hspace{1pt}\)で最小値となります。
\(f(4)\hspace{1pt}\)の値は $$\begin{aligned} f(4) & = \sqrt{4} - \log 4\\[0.5em] & =2 - \log 2^2\\[0.5em] & =2 - 2\log 2\\[0.5em] & =2(1 - \log 2)\\[0.5em] \end{aligned}$$ であり、\( 0 < \log 2 < 1\hspace{1pt}\)であることから $${f(4) = 2(1 - \log 2) > 0}$$ となります。
すなわち、関数\(\hspace{1pt}f(x)\hspace{1pt}\)は\(\hspace{3pt}x \geqq 1\hspace{1pt}\)において\(\hspace{1pt}f(x) \geqq 0\hspace{1pt}\)であるため、問題の不等式 $${ \sqrt{x} \geqq \log x \hspace{5pt}\left(\hspace{1pt} x \geqq 1 \right)}$$ は成り立ちます。
【(2)の解答】
(1)の結果を利用し、はさみうちの原理から極限値\(\displaystyle \hspace{1pt}\lim_{x \rightarrow \infty}\frac{\log x}{x} \hspace{1pt}\)を求めます。
\(x \geqq 1\hspace{1pt}\)であるとき、\(\log x \geqq 0\hspace{1pt}\)であるため、(1)の結果から $${ 0 \leqq \log x \leqq \sqrt{x}}$$ すなわち $${ 0 \leqq \frac{\log x}{x} \leqq \frac{\sqrt{x}}{x}}$$ となります。
はさみうちの原理から、\(\displaystyle \lim_{x \rightarrow \infty}\frac{\sqrt{x}}{x}=0\hspace{1pt}\)であることから $${\lim_{x \rightarrow \infty}\frac{\log x}{x} = 0}$$ となります。
【(3)の解答】
(2)の結果を利用して、\(\displaystyle y = \frac{\log x}{ x}\hspace{1pt}\)のグラフをかきます。
\(\displaystyle {f(x)=\frac{\log x}{ x}}\) とすると
となります。
次に \({f'(x)=0}\) を満たす\(\hspace{1pt}x\hspace{1pt}\)を求めると
$${1 - \log x = 0}$$ すなわち $$\begin{aligned} \hspace{10pt}\log x & =1\hspace{10pt}\\[0.5em] x & = e\\[0.5em] \end{aligned}$$ となります。
ここで、\(\displaystyle x = e \hspace{1pt}\)の前後における\(\displaystyle{\hspace{1pt}f'(x)\hspace{1pt}}\)の符号を調べます。
\({\displaystyle 0 < x < e}\) のとき \({f'(x) > 0}\)
\({\displaystyle x > e}\) のとき \({f'(x) < 0}\)
よって、関数 \(\displaystyle {f(x)}\) は\(\displaystyle {\hspace{2pt}x=e}\) で極大値をとります。
以上から増減表を作ると 以下のようになります。
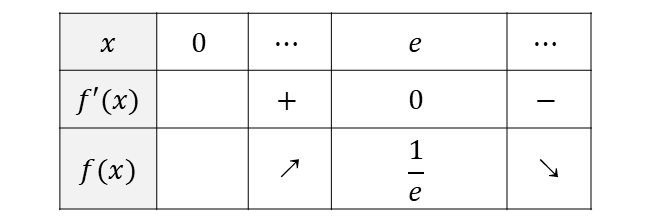
また、(2)の結果から\(\displaystyle \hspace{1pt}\lim_{x \rightarrow \infty}\frac{\log x}{x} = 0\hspace{1pt}\)となります。したがって、\(x\hspace{1pt}\)軸が漸近線となります。
さらに\(\displaystyle \hspace{1pt}\lim_{x \rightarrow +0}\log x = - \infty\)、\(\displaystyle \lim_{x \rightarrow +0}\frac{1}{x}= \infty\) であることから \(\displaystyle \lim_{x \rightarrow +0}\frac{\log x}{x}= -\infty\) となります。
すなわち、\(y\hspace{1pt}\)軸が漸近線となります。
以上から、\(\displaystyle y = \frac{\log x}{ x}\hspace{1pt}\)のグラフは以下のようになります。

【(4)の解答】
(3)のグラフを利用して、\(\displaystyle e^\pi \hspace{1pt}\)と\(\hspace{1pt}\pi^e\hspace{1pt}\)の大小関係を導きます。
\(\displaystyle y = \frac{\log x}{ x}\hspace{1pt}\)のグラフから $${\frac{\log x}{ x} \leqq \frac{\log e}{e}}$$ であり、等号が成り立つのは\(\hspace{1pt}x=e\hspace{1pt}\)のときとなります。
\(\displaystyle {x = \pi}\) とすると $${\frac{\log \pi}{ \pi} < \frac{\log e}{e}}$$ すなわち $${e \log \pi < \pi \log e}$$ $${ \log \pi^e < \log e^\pi}$$ したがって $${ \pi^e < e^\pi}$$ となります。