√x+√y=√a上の接線の問題

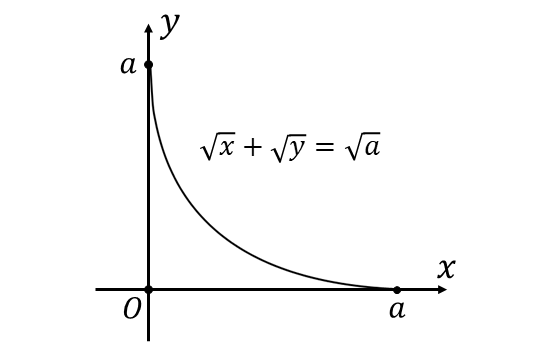
【(1)解答のポイント】
陰関数のグラフを書く問題は、まず『対称性』と『定義域』を調べます。

本問では\(\hspace{1pt}x , y\hspace{1pt}\)は根号に含まれるため\(\hspace{2pt}x \geqq 0 , y \geqq 0\hspace{1pt}\)となります。

また、 $${\sqrt{a} - \sqrt{x} \geqq 0}$$ すなわち $${0 \leqq x \leqq a}$$ また、\(\hspace{1pt}y\hspace{1pt}\)についても同様に $${0 \leqq y \leqq a}$$ と定義域を求めることができます。

求められた定義域の範囲で $${y = (\sqrt{a} - \sqrt{x})^2 }$$ の増減表をかくことでグラフを作成します。

【(2)解答のポイント】
点\(\hspace{1pt}P(x_1 , y_1 )\hspace{1pt}\)における接線の方程式 $${y = f'(x_1)(x - x_1) +y_1 }$$ が\(\hspace{1pt}x\hspace{1pt}\)軸, \(y\hspace{1pt}\)軸と交わる点の座標を求め、\(OA + OB\hspace{1pt}\)が一定であることを確かめます。

【(1)の解答】
まず、曲線\(\hspace{1pt}C : \sqrt{x} + \sqrt{y} = \sqrt{a}\hspace{1pt}\)の定義域を調べます。

\(x , y\hspace{1pt}\)は根号に含まれるため\(\hspace{1pt}x \geqq 0 , y \geqq 0\hspace{1pt}\)となります。

また、問題の曲線の式を変形すると $${\sqrt{y} = \sqrt{a} - \sqrt{x} }$$ \(\sqrt{y} \geqq 0\hspace{1pt}\)であるため $${\sqrt{a} - \sqrt{x} \geqq 0}$$ すなわち $${ x \leqq a}$$ となります。\(\hspace{1pt}x \geqq 0\hspace{1pt}\)と共通部分をとると $${ 0 \leqq x \leqq a}$$ となります。\(\hspace{1pt}y\hspace{1pt}\)についても同様に $${ 0 \leqq y \leqq a}$$ となります。

\(f(x)= (\sqrt{a} - \sqrt{x} )^2\hspace{1pt}\)として関数\(\hspace{1pt}f(x)\hspace{1pt}\)の導関数を求めると $$\begin{aligned} f'(x) & = 2(\sqrt{a} - \sqrt{x} )\cdot \left(-\frac{1}{2 \sqrt{x}} \right)\\[1em] & = -\frac{ \sqrt{a} - \sqrt{x} }{\sqrt{x}} \\[1em] \end{aligned}$$ となります。

また、関数\(\hspace{1pt}f(x)\hspace{1pt}\)の第二次導関数を求めると

すなわち、\( 0 < x < a\hspace{1pt}\)において\(\hspace{1pt}f'(x) < 0\hspace{1pt}\)であるため関数\(\hspace{1pt}f(x)\hspace{1pt}\)は単調に減少します。

また、\( 0 < x < a\hspace{1pt}\)において\(\hspace{1pt}f''(x) > 0\hspace{1pt}\)であるため、関数\(\hspace{1pt}f(x)\hspace{1pt}\)は下に凸のグラフとなります。

ここで、一次導関数の極限値を調べると $$\begin{aligned} \hspace{10pt}\lim_{x \rightarrow +0} f'(x) & = - \infty\hspace{10pt}\\[1.2em] \lim_{x \rightarrow a-0} f'(x) & = 0\hspace{10pt}\\[1.2em] \end{aligned}$$ となります。

すなわち、\(x = 0\hspace{1pt}\)では曲線が\(\hspace{1pt}y\hspace{1pt}\)軸に接し、\(x = a\hspace{1pt}\)では曲線が\(\hspace{1pt}x\hspace{1pt}\)軸に接することが分かります。

以上から、問題の関数のグラフは以下のようになります。

【(2)の解答】

曲線\(\hspace{1pt}\sqrt{x} + \sqrt{y} = \sqrt{a}\hspace{1pt}\)上の接点を\(\hspace{1pt}P(x_1 , y_1)\hspace{1pt}\)とします。

また、接線が\(\hspace{1pt}x\hspace{1pt}\)軸,\(\hspace{1pt}y\hspace{1pt}\)軸と交わる点を以下のようにそれぞれ\(\hspace{1pt}A,B\hspace{1pt}\)とします。

(1)の計算から $$\begin{aligned} y' & = -\frac{ \sqrt{a} - \sqrt{x} }{\sqrt{x}}\\[1em] & = -\sqrt{\frac{ y }{x}}\\[1em] \end{aligned}$$

すなわち、点\(\hspace{1pt}P\hspace{1pt}\)における接線の方程式は $${y = -\sqrt{\frac{y_1}{ x_1}}(x - x_1) +y_1 \cdots (1)}$$ となります。

ここで、(1)式から点\(\hspace{1pt}A\hspace{1pt}\)の座標を求めると、\(y=0\hspace{1pt}\)を代入して $${x = \sqrt{x_1 y_1 } + x_1}$$ となります。

すなわち\(\hspace{1pt}OA\hspace{1pt}\)の長さは $${OA = \sqrt{x_1 y_1 } + x_1}$$ となります。

また、(2)式から点\(\hspace{1pt}B\hspace{1pt}\)の座標を求めると、\(x=0\hspace{1pt}\)を代入して $${y = \sqrt{x_1 y_1 } + y_1}$$ となります。

すなわち\(\hspace{1pt}OB\hspace{1pt}\)の長さは $${OB = \sqrt{x_1 y_1 } + y_1}$$ となります。

したがって、\(OA + OB\hspace{1pt}\)は

であることから、\(\hspace{1pt}OA + OB\hspace{1pt}\)は一定となります。