場合の数・確率ランダム問題集

【難易度★】
　高校数学の教科書の基本的な例題レベルの難易度です。
　基本を理解できているかのチェックをしたい方向けです。

【難易度★★】
　高校数学の教科書の演習・章末問題のレベルの難易度です。
　数学の定期試験の対策がしたい方向けです。

【難易度★★★】
　高校数学の教科書の問題と比べ、やや難しい難易度です。
　入試問題の基礎的なレベルの問題を解きたい人向けです。

【ランダムに出題】
従来の問題集では、問題の種類ごとに整理されている形式が一般的であるため、解き始める前に『解法のパターン』を分かった上で解くことになります。

そのため、従来の問題集では問題文から解法を見抜く力を養うことができないという欠点があります。

本問題集では、問題をランダムに出題することで定期テスト・入試問題で必須となる "問題文から解法を見抜く力" が付くように意図しています。

また、本ページの下部に問題の一覧も掲載しているため、通常の問題集としても活用できます。

【ヒントボタン】
本問題集では、問題の下のヒントボタンを押すことで解答のヒントが見れるようにしています。

『自力で解けそうな場合はヒントなしで解く』、『手も足も出ない場合にヒントを見る』とすることで "段階的にレベルアップ" できることを意図しています。

【問題数】
本問題集では、高校数学の場合の数・確率に関連する問題を59問掲載しています。

【場合の数の基礎】
問題1 : 大小\(\hspace{1pt}2\hspace{1pt}\)個のサイコロを投げるとき、以下の場合の数を求めよ
　(1) 目の和が\(\hspace{1pt}8\hspace{1pt}\)
　(2) 目の和が\(\hspace{1pt}9\hspace{1pt}\)以上
　(3) 目の和が\(\hspace{1pt}5\hspace{1pt}\)の倍数

【順列】
問題2 : 男子\(\hspace{1pt}4\hspace{1pt}\)人,女子\(\hspace{1pt}3\hspace{1pt}\)人が一列に並ぶとき、以下の方法の総数を求めよ
　　(1)男子が両端となる並び方
　　(2)女子\(\hspace{1pt}3\hspace{1pt}\)人が隣り合う並び方
　　(3)男子と女子が交互に並ぶ並び方

問題3 : 男子\(\hspace{1pt}4\hspace{1pt}\)人,女子\(\hspace{1pt}3\hspace{1pt}\)人が並ぶとき、以下の方法の総数を求めよ
　　(1) \(\hspace{1pt}7\hspace{1pt}\)人全員が一列に並ぶ
　　(2) 男子が両端となる並び方
　　(3) 少なくとも一端が女子となる並び方

【順列(数字を並べて整数を作る)】
問題4 : \(1,2,3,4,5\hspace{1pt}\)の\(\hspace{1pt}5\hspace{1pt}\)個の数字から異なる数字を選び並べるとき、以下の整数は何通りできるか求めよ
　　(1) \(4\hspace{1pt}\)桁の偶数
　　(2) \(3\hspace{1pt}\)桁の奇数

問題5 : \(0,1,2,3,4,5\hspace{1pt}\)の\(\hspace{1pt}6\hspace{1pt}\)個の数字から異なる数字を選び並べるとき、以下の数は何通りできるか求めよ
　　(1) \(4\hspace{1pt}\)桁の整数
　　(2) \(4\hspace{1pt}\)桁の奇数

【円順列・じゅず順列】
問題6 : 異なる\(\hspace{1pt}7\hspace{1pt}\)個の宝石から、以下の種類は何通りできるか求めよ
　　(1) 宝石を机の上で円形に並べる
　　(2) 宝石を糸で繋いでネックレスを作る

問題7 : 女子4人と男子2人が円形に並ぶとき、以下の方法は何通りできるか求めよ
　　(1) 男子\(\hspace{1pt}2\hspace{1pt}\)人が向かい合う
　　(2) 男子\(\hspace{1pt}2\hspace{1pt}\)人が隣り合う
　　(3) 男子\(\hspace{1pt}2\hspace{1pt}\)人が隣り合わない

【重複順列】
問題8 : \(8\hspace{1pt}\)人を以下のように分ける方法が何通りか求めよ
　　(1) \(\hspace{1pt}A\hspace{1pt}\)または\(\hspace{1pt}B\hspace{1pt}\)の部屋に分ける
　　　　ただし、\(1\hspace{1pt}\)人も入らない部屋があってもよいとする
　　(2) グループ\(\hspace{1pt}A\hspace{1pt}\)または\(\hspace{1pt}B\hspace{1pt}\)に分ける
　　(3) \(\hspace{1pt}2\hspace{1pt}\)つのグループに分ける

問題9 : 集合\(\hspace{1pt}\{a ,b ,c ,d ,e , f ,g\}\hspace{1pt}\)の部分集合の個数を求めよ

問題10 : \(0,1,2,3,4,5\hspace{1pt}\)の\(\hspace{1pt}6\hspace{1pt}\)個の数字から異なる数字を重複を許して選び並べるとき、以下の数は何通りできるか求めよ
　　(1) \(4\hspace{1pt}\)桁の整数
　　(2) \(4\hspace{1pt}\)桁の偶数
　　(3) \(4\hspace{1pt}\)桁の奇数

【組み合わせ】
問題11 : 男子\(\hspace{1pt}4\hspace{1pt}\)人,女子\(\hspace{1pt}3\hspace{1pt}\)人について以下の方法は何通りか求めよ
　　(1) \(7\hspace{1pt}\)人から\(\hspace{1pt}4\hspace{1pt}\)人を選び並べる
　　(2) \(7\hspace{1pt}\)人から\(\hspace{1pt}4\hspace{1pt}\)人を選ぶ
　　(3) 男子\(\hspace{1pt}2\hspace{1pt}\)人と女子\(\hspace{1pt}2\hspace{1pt}\)人を選ぶ
　　(4) \(4\hspace{1pt}\)人を選ぶとき、少なくとも\(\hspace{1pt}1\hspace{1pt}\)人女子を選ぶ

問題12 : 正七角形について以下の総数を求めよ
　　(1) \(\hspace{1pt}3\hspace{1pt}\)つの頂点を結んで作られる三角形の数
　　(2) \(\hspace{1pt}4\hspace{1pt}\)つの頂点を結んで作られる四角形の数
　　(3) 対角線の本数

【同じものを含む順列】
問題13 : \(A\hspace{1pt}\)を\(\hspace{1pt}2\hspace{1pt}\)個、\(B\hspace{1pt}\)を\(\hspace{1pt}3\hspace{1pt}\)個、\(C\hspace{1pt}\)を\(\hspace{1pt}3\hspace{1pt}\)個の\(\hspace{1pt}8\hspace{1pt}\)文字全てを使った文字列について以下の方法は何通りか求めよ
　　(1) 文字列の数
　　(2) 両端が\(\hspace{1pt}A\hspace{1pt}\)の文字列の数
　　(3) \(\hspace{1pt}A\hspace{1pt}\)が隣り合う文字列の数

問題14 : \(1,1,2,2,2,3,3,3\hspace{1pt}\)から全ての数字を使用して\(\hspace{1pt}8\hspace{1pt}\)桁の数を作るとき、以下の方法は何通りか求めよ
　　(1) 整数の数
　　(2) 偶数の数

【重複を許して取る組み合わせ】
問題15 : イチゴ、りんご、みかんの\(\hspace{1pt}3\hspace{1pt}\)種類の果物から重複を許して\(\hspace{1pt}6\hspace{1pt}\)個を取る組み合わせは何通りか求めよ

【男女が並ぶ順列】
問題1 : 男子\(\hspace{1pt}3\hspace{1pt}\)人,女子\(\hspace{1pt}3\hspace{1pt}\)人が交互に並ぶときの並び方の総数を求めよ

【数字を並べて整数を作る】
問題2 : \(0,1,2,3,4,5\hspace{1pt}\)の\(\hspace{1pt}6\hspace{1pt}\)個の数字から異なる数字を選び並べるとき、\(4\hspace{1pt}\)桁の偶数は何通りできるか求めよ

問題3 : \(1,2,3,4,5,6\hspace{1pt}\)の\(\hspace{1pt}6\hspace{1pt}\)個の数字から異なる数字を選ぶとき、\(2300\hspace{1pt}\)より大きい\(\hspace{1pt}4\hspace{1pt}\)桁の数字は何通りできるか求めよ

【円順列・じゅず順列】
問題4 : \(\hspace{1pt}7\hspace{1pt}\)個の宝石から\(\hspace{1pt}5\hspace{1pt}\)個を選び、机の上で円形に並べる方法は何通りか求めよ

【重複順列】
問題5 : \(a,b,c,d\hspace{2pt}\)の\(\hspace{1pt}4\hspace{1pt}\)個の文字から重複を許して選び並べるとき、\(\hspace{1pt}1\hspace{1pt}\)文字以上\(\hspace{1pt}4\hspace{1pt}\)文字以下の単語は何通りできるか求めよ

【組み合わせ】
問題6 : \(\hspace{1pt}12\hspace{1pt}\)人を以下のように分けるの方法は何通りか求めよ
　　(1) \(5\hspace{1pt}\)人、\(4\hspace{1pt}\)人、\(3\hspace{1pt}\)人に分ける
　　(2) \(4\hspace{1pt}\)人ずつ\(\hspace{1pt}A,B,C\hspace{1pt}\)のグループに分ける
　　(3) \(4\hspace{1pt}\)人ずつ\(\hspace{1pt}3\hspace{1pt}\)グループに分ける
　　(4) \(6\hspace{1pt}\)人、\(3\hspace{1pt}\)人、\(3\hspace{1pt}\)人に分ける

【同じものを含む順列】
問題7 : \(0,1,1,2,2,2,2\hspace{1pt}\)から全ての数字を使用して\(\hspace{1pt}7\hspace{1pt}\)桁の数を作るとき、整数は何通りできるか求めよ

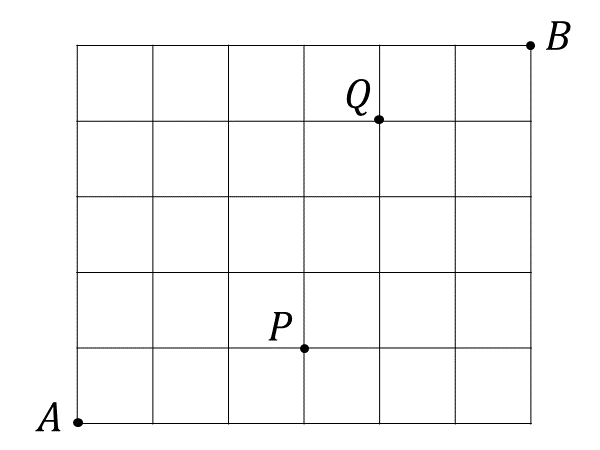
問題8 : 下図のように東西に\(\hspace{1pt}6\hspace{1pt}\)本、南北に\(\hspace{1pt}7\hspace{1pt}\)本の道が通っている。
　以下のような方法で地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)まで最短経路で行く道順の数を求めよ
　　(1) 全ての道を使う
　　(2) 地点\(\hspace{1pt}P\hspace{1pt}\)を通る
　　(3) 地点\(\hspace{1pt}P\hspace{1pt}\)を通らない
　　(4) 地点\(\hspace{1pt}P\hspace{1pt}\)と地点\(\hspace{1pt}Q\hspace{1pt}\)を通る

【重複を許して取る組み合わせ】
問題9 : \(\hspace{1pt}9\hspace{1pt}\)個のりんごを\(\hspace{1pt}3\hspace{1pt}\)人に分配する方法は何通りか求めよ
　ただし、少なくとも\(\hspace{1pt}1\hspace{1pt}\)個はりんごを受け取るとする。

問題10 : 次の条件を満たす整数の組\(\hspace{1pt}(x,y,z)\hspace{1pt}\)は何通りあるか求めよ
　(1) \(x + y + z = 8 ,\hspace{2pt} x \geqq 0 ,\hspace{2pt} y \geqq 0 , \hspace{2pt} z \geqq 0\)
　(2) \(x + y + z = 8 ,\hspace{2pt} x \geqq 1 , \hspace{2pt} y \geqq 1 ,\hspace{2pt} z \geqq 1\hspace{1pt}\)

【数字を並べて整数を作る】
問題1 : \(1,2,3,4,5,6\hspace{1pt}\)の\(\hspace{1pt}6\hspace{1pt}\)個の数字から異なる数字を\(\hspace{1pt}5\hspace{1pt}\)個選び並べるとき、以下の数は何通りできるか求めよ
　(1) \(\hspace{1pt}2\hspace{1pt}\)の倍数
　(2) \(\hspace{1pt}3\hspace{1pt}\)の倍数
　(3) \(\hspace{1pt}6\hspace{1pt}\)の倍数
　

【繰り返し数字を選ぶ問題】
問題2 : \(1\hspace{1pt}\)から\(\hspace{1pt}n\hspace{1pt}\)までの番号が振られた玉が入った袋がある。
この袋から玉を\({\hspace{1pt}1\hspace{1pt}}\)つ取り出して、数字を確認して元に戻すという操作を\({\hspace{1pt}3\hspace{1pt}}\)回繰り返す。出た数字を順に\({\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt}}\)とするとき、以下の場合の数を求めよ。ただし、\(n\hspace{1pt}\)は\(\hspace{1pt}3\hspace{1pt}\)以上の整数とする。
　(1) \({ A < B < C \hspace{2pt}}\)となる場合の数
　(2) \({ A = B < C \hspace{2pt}}\)となる場合の数
　(3) \({ A \leqq B \leqq C \hspace{2pt}}\)となる場合の数
　

【頂点を結んでできる図形の個数】
問題3 : 正\(\hspace{1pt}N\hspace{1pt}\)角形について以下の総数を求めよ(ただし、\(N\hspace{1pt}\)は\(\hspace{1pt}N \geqq 4\hspace{1pt}\)を満たす自然数とする)
　　(1) \(\hspace{1pt}3\hspace{1pt}\)つの頂点を結んで作られる三角形の数
　　(2) \(\hspace{1pt}4\hspace{1pt}\)つの頂点を結んで作られる四角形の数
　　(3) 対角線の本数
　　(4) 対角線の交点のうち、正\(\hspace{1pt}N\hspace{1pt}\)角形の内部にある交点の数
　

【円周上から3つの点を選ぶ三角形の数】
問題4 : 円周上を\(\hspace{1pt}12\hspace{1pt}\)等分する点\(\hspace{1pt}A_i\hspace{1pt}\)\(\hspace{1pt}(1 \leqq i \leqq 12)\hspace{1pt}\)がある。これらの点から異なる\(\hspace{1pt}3\hspace{1pt}\)点を選び、下図のように選ばれた点を頂点とする三角形を作るとする。
　例えば、下図は点\(\hspace{1pt}A_1 , A_4 , A_8\hspace{1pt}\)を選んだときの三角形である。

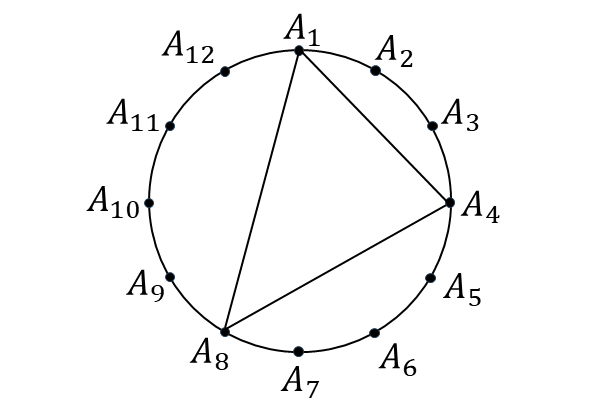
　このとき、以下のような三角形が何通りできるか求めよ。
　(1) 三角形の数
　(2) 正三角形の数
　(3) 正三角形でない二等辺三角形の数
　(4) 直角三角形の数
　

【組み分けの問題】
問題5 : \(\hspace{1pt}A , B , C , D , E\hspace{1pt}\)の\(\hspace{1pt}5\hspace{1pt}\)人全員を\(\hspace{1pt}2\hspace{1pt}\)つ以上のグループに分けるとき、以下のような分け方は何通りか求めよ。
　ただし、グループ同士に区別はないとする。また、どのグループも少なくとも\(\hspace{1pt}1\hspace{1pt}\)人は含むとする。
　　(1) \(A\hspace{1pt}\)が\(\hspace{1pt}4\hspace{1pt}\)人のグループにいる分け方
　　(2) \(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)人のグループにいる分け方
　　(3) \(A\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)人のグループにいる分け方
　　(4) 全てのグループの分け方

【整数の組の数を求める問題】
問題6 : 次の条件を満たす正の整数の組\(\hspace{1pt}(x,y,z)\hspace{1pt}\)は何通りあるか求めよ。ただし、\(n\hspace{1pt}\)は\(\hspace{1pt}3\hspace{1pt}\)以上の整数とする。
　　(1) \(x + y + z = 9 \)
　　(2) \(x + y + z = n \)
　　(3) \(x + y + z \leqq n \)
　

【組み合わせ\(\hspace{1pt}{}_n C_r\hspace{1pt}\)を含む方程式】
問題7 : 次の式を満たす整数\(\hspace{1pt}n\hspace{1pt}\)を求めよ。ただし、\(n\hspace{1pt}\)は\(\hspace{1pt}n \geqq 2\hspace{1pt}\)を満たす整数とする
\(\hspace{2pt}{}_{n+2}C_{n-1} + {}_{n+1}C_{n-1} + {}_{2(n+1)}C_{2n+1} = 40\)

【確率の基礎】
問題1 : 大小\(\hspace{1pt}2\hspace{1pt}\)個のサイコロを振るとき、以下の確率を求めよ
　　(1) 目の和が\(\hspace{1pt}8\hspace{1pt}\)
　　(2) 目の和が\(\hspace{1pt}9\hspace{1pt}\)以上
　　(3) 目の和が\(\hspace{1pt}3\hspace{1pt}\)の倍数
　　(4) 目の積が奇数

【排反事象・余事象】
問題2 : \(\hspace{1pt}1\hspace{1pt}\)から\(\hspace{1pt}100\hspace{1pt}\)までの数字の振られたカードを一回引くとき、数字が以下のようになる確率を求めよ
　　(1) \(\hspace{1pt}3\hspace{1pt}\)の倍数である確率
　　(2) \(\hspace{1pt}3\hspace{1pt}\)の倍数でない確率
　　(3) \(\hspace{1pt}3\hspace{1pt}\)で割ると\(\hspace{1pt}1\hspace{1pt}\)余る数字である確率

問題3 : 赤玉\(\hspace{1pt}3\hspace{1pt}\)個と白玉\(\hspace{1pt}4\hspace{1pt}\)個が入っている袋がある。この袋から同時に\(\hspace{1pt}2\hspace{1pt}\)個の玉を取り出すとき、以下の確率を求めよ
　　(1) \(\hspace{1pt}2\hspace{1pt}\)個とも赤玉である確率
　　(2) \(\hspace{1pt}2\hspace{1pt}\)個とも同じ色である確率

問題4 : \(12\hspace{1pt}\)本のうち当たりが\(\hspace{1pt}3\hspace{1pt}\)本入っているくじから、同時に\(\hspace{1pt}4\hspace{1pt}\)本引くとき、以下の確率を求めよ
　　(1) 当たりを\(\hspace{1pt}2\hspace{1pt}\)本だけ引く確率
　　(2) 当たりを\(\hspace{1pt}2\hspace{1pt}\)本以上引く確率
　　(3) 少なくとも\(\hspace{1pt}1\hspace{1pt}\)本は当たりを引く確率

【独立な試行の確率】
問題5 : \(10\hspace{1pt}\)本のうち当たりが\(\hspace{1pt}2\hspace{1pt}\)本入っているくじから\(\hspace{1pt}1\hspace{1pt}\)本引き、結果を確認して元に戻すことを\(\hspace{1pt}3\hspace{1pt}\)回繰り返すとき、以下の確率を求めよ
　　(1) \(\hspace{1pt}3\hspace{1pt}\)回とも当たりを引く確率
　　(2) \(\hspace{1pt}3\hspace{1pt}\)回目に初めて当たりを引く確率
　　(3) 少なくとも\(\hspace{1pt}1\hspace{1pt}\)回は当たりを引く確率

問題6 : \(5\hspace{1pt}\)個の赤玉と\(\hspace{1pt}3\hspace{1pt}\)個の白玉が入っている袋がある。この袋から\(\hspace{1pt}1\hspace{1pt}\)個の玉を引き、結果を確認して元に戻すことを\(\hspace{1pt}3\hspace{1pt}\)回繰り返すとき、以下の確率を求めよ
　　(1) \(\hspace{1pt}3\hspace{1pt}\)回とも赤玉を引く確率
　　(2) \(\hspace{1pt}3\hspace{1pt}\)回とも同じ色を引く確率
　　(3) 異なる色の玉を引く確率

【反復試行の確率】
問題7 : \(10\hspace{1pt}\)本のうち当たりが\(\hspace{1pt}2\hspace{1pt}\)本入っているくじから、\(1\hspace{1pt}\)本引いて結果を確認して戻すことを\(\hspace{1pt}5\hspace{1pt}\)回繰り返すとき、以下の確率を求めよ
　　(1) 当たりを\(\hspace{1pt}2\hspace{1pt}\)回引く確率
　　(2) 当たりを\(\hspace{1pt}4\hspace{1pt}\)回以上引く確率

問題8 : \(1\hspace{1pt}\)個のサイコロを\(\hspace{1pt}6\hspace{1pt}\)回振るときに、以下の確率を求めよ
　　(1) \(3\hspace{1pt}\)の倍数の目が\(\hspace{1pt}4\hspace{1pt}\)回出る確率
　　(2) 偶数の目の出る回数が\(\hspace{1pt}2\hspace{1pt}\)回以下の確率

問題9 : \(4\hspace{1pt}\)個の赤玉と\(\hspace{1pt}2\hspace{1pt}\)個の白玉の入った袋がある。この袋から玉を\(\hspace{1pt}1\hspace{1pt}\)個取り出して色を確認して戻す試行を\(\hspace{1pt}6\hspace{1pt}\)回繰り返すとき、以下の確率を求めよ
　　(1) 赤玉を\(\hspace{1pt}2\hspace{1pt}\)回引く確率
　　(2) 赤玉を\(\hspace{1pt}2\hspace{1pt}\)回以上引く確率

【条件付き確率】
問題10 : \(10\hspace{1pt}\)本のうち当たりが\(\hspace{1pt}3\hspace{1pt}\)本入っているくじから、\(1\hspace{1pt}\)本ずつ\(\hspace{1pt}2\hspace{1pt}\)回続けてくじを引く。ただし、引いたくじは戻さないとする。このとき、以下の確率を求めよ
　　(1) 当たりを\(\hspace{1pt}2\hspace{1pt}\)本続けて引く確率
　　(2) \(1\hspace{1pt}\)本目が外れ、\(2\hspace{1pt}\)本目が当たりを引く確率

問題11 : 赤玉が\(\hspace{1pt}5\hspace{1pt}\)個、白玉が\(\hspace{1pt}3\hspace{1pt}\)個入った袋がある。玉を\(\hspace{1pt}1\hspace{1pt}\)個ずつ\(\hspace{1pt}3\hspace{1pt}\)回続けてを引く。ただし、引いた玉は戻さないとする。このとき、以下の確率を求めよ
　　(1) 同じ色の玉を\(\hspace{1pt}3\hspace{1pt}\)回続けて引く確率
　　(2) \(3\hspace{1pt}\)回目に白玉を引く確率

【排反事象・余事象】
問題1 : \(\hspace{1pt}1\hspace{1pt}\)から\(\hspace{1pt}100\hspace{1pt}\)までの数字の振られたカードを一回引くとき、数字が以下のようになる確率を求めよ
　　(1) \(\hspace{1pt}3\hspace{1pt}\)の倍数または\(\hspace{1pt}5\hspace{1pt}\)の倍数の確率
　　(2) \(\hspace{1pt}3\hspace{1pt}\)の倍数でも\(\hspace{1pt}5\hspace{1pt}\)でもない確率

問題2 : 赤玉\(\hspace{1pt}5\hspace{1pt}\)個と白玉\(\hspace{1pt}4\hspace{1pt}\)個が入っている袋がある。この袋から同時に\(\hspace{1pt}3\hspace{1pt}\)個の玉を取り出すとき、以下の確率を求めよ
　　(1) \(\hspace{1pt}3\hspace{1pt}\)個とも同じ色である確率
　　(2) 少なくとも\(\hspace{1pt}1\hspace{1pt}\)個ずつ赤玉と白玉を選ぶ確率

問題3 : 赤玉\(\hspace{1pt}5\hspace{1pt}\)個、白玉\(\hspace{1pt}4\hspace{1pt}\)個、青玉\(\hspace{1pt}3\hspace{1pt}\)個が入っている袋がある。この袋から同時に\(\hspace{1pt}3\hspace{1pt}\)個の玉を取り出すとき、以下の確率を求めよ
　　(1) 赤玉が\(\hspace{1pt}1\hspace{1pt}\)個以下となる確率
　　(2) \(3\hspace{1pt}\)個とも同じ色となる確率
　　(3) 取り出した玉の色が\(\hspace{1pt}2\hspace{1pt}\)色である確率

問題4 : 大中小\(\hspace{1pt}3\hspace{1pt}\)個のサイコロを振るとき、以下の確率を求めよ
　　(1) サイコロの目の最大値が\(\hspace{1pt}3\hspace{1pt}\)以下の確率
　　(2) サイコロの目の最大値が\(\hspace{1pt}4\hspace{1pt}\)の確率

【独立な事象の確率】
問題5 : \(4\hspace{1pt}\)個の赤玉と\(\hspace{1pt}3\hspace{1pt}\)個の白玉が入っている袋\(\hspace{1pt}P\hspace{1pt}\)と
　\(5\hspace{1pt}\)個の赤玉と\(\hspace{1pt}2\hspace{1pt}\)個の白玉が入っている袋\(\hspace{1pt}Q\hspace{1pt}\)がある。
　袋\(\hspace{1pt}P\hspace{1pt}\)から\(\hspace{1pt}1\hspace{1pt}\)個、袋\(\hspace{1pt}Q\hspace{1pt}\)から\(\hspace{1pt}2\hspace{1pt}\)個の玉を引くとき、以下の確率を求めよ
　　(1) 赤玉を\(\hspace{1pt}\hspace{1pt}1\hspace{1pt}\)個、白玉を\(\hspace{1pt}\hspace{1pt}2\hspace{1pt}\)個を引く確率
　　(2) 玉の色が全て同じ確率

問題6 : サイコロを\(\hspace{1pt}N\hspace{1pt}\)回振るとき、以下の確率を求めよ。ただし、\(\hspace{1pt}N\hspace{1pt}\)は\(\hspace{1pt}N \geqq 2\hspace{1pt}\)を満たす整数とする。
　　(1) サイコロの目の積が偶数となる確率
　　(2) サイコロの目の積が\(\hspace{1pt}3\hspace{1pt}\)の倍数となる確率

【反復試行の確率】
問題7 : \(A\hspace{1pt}\)と\(\hspace{1pt}B\hspace{1pt}\)のどちらかが先に\(\hspace{1pt}3\hspace{1pt}\)勝したら優勝する試合を行った。引き分けはないものとし、\(A\hspace{1pt}\)は\(\hspace{1pt}B\hspace{1pt}\)に対して\(\displaystyle\hspace{2pt}\frac{1}{3}\hspace{2pt}\)の確率で勝つとする。
　　(1) \(3\hspace{1pt}\)回戦目で優勝が決まる確率
　　(2) \(4\hspace{1pt}\)回戦目で\(A\hspace{1pt}\)の優勝が決まる確率
　　(3) \(A\hspace{1pt}\)が優勝する確率

問題8 : 数直線上の原点に点\(\hspace{1pt}P\hspace{1pt}\)がある。\(1\hspace{1pt}\)個のサイコロを投げ、\(3\hspace{1pt}\)の倍数の目が出たときに\(\hspace{2pt}+1\hspace{2pt}\)、\(3\hspace{2pt}\)の倍数以外の目が出たときに\(\hspace{1pt}-1\hspace{1pt}\)だけ移動するとする。
　サイコロを\(\hspace{1pt}6\hspace{1pt}\)回投げるとき、以下の確率を求めよ。
　　(1) 点\(\hspace{1pt}P\hspace{1pt}\)が原点にある確率
　　(2) 点\(\hspace{1pt}P\hspace{1pt}\)が\(\hspace{1pt}4\hspace{1pt}\)以上となる確率

問題9 : \(12\hspace{1pt}\)本のうち当たりが\(\hspace{1pt}3\hspace{1pt}\)本入っているくじから\(\hspace{1pt}1\hspace{1pt}\)本を引き、結果を確認して元に戻す操作を\(\hspace{1pt}5\hspace{1pt}\)回繰り返す。
　当たりを引くと\(\hspace{1pt}+3\hspace{1pt}\)点、はずれを引くと\(\hspace{1pt}-2\hspace{1pt}\)点であるとき、以下の確率を求めよ。
　　(1) 点が\(\hspace{1pt}10\hspace{1pt}\)点になる確率
　　(2) 点が\(\hspace{1pt}0\hspace{1pt}\)点以下になる確率

【3個のサイコロの確率の問題】
問題1 : \(3\hspace{1pt}\)個のサイコロを同時に振ったときの目の積について以下の確率を求めよ。
　(1) 目の積が\(\hspace{1pt}3\hspace{1pt}\)の倍数になる確率
　(2) 目の積が\(\hspace{1pt}9\hspace{1pt}\)の倍数になる確率
　(3) 目の積が\(\hspace{1pt}36\hspace{1pt}\)になる確率
　(4) 目の積が素数になる確率
　(5) 目の積または和が\(\hspace{1pt}3\hspace{1pt}\)の倍数になる確率
　

問題2 : サイコロを\(\hspace{1pt}3\hspace{1pt}\)回続けて振ったとき、出た目の順に\(\hspace{1pt}x,y,z\hspace{1pt}\)とする。このとき、以下の式が成り立つ確率を求めよ
$$ \begin{aligned} (1) \hspace{10pt} & (x-y)(y-z)(z-x) = 0\\[0.3em] (2) \hspace{10pt} & \frac{1}{x} + \frac{1}{y} \geqq 1\\[0.7em] (3) \hspace{10pt} & \frac{1}{x} + \frac{1}{y} \geqq \frac{1}{z}\\[0.7em] \end{aligned} $$

【二次方程式の解の条件と確率の問題】
問題3 : サイコロを\(\hspace{1pt}3\hspace{1pt}\)回投げて、出た目の順に\(\hspace{1pt}a , b ,c\hspace{1pt}\)とする。このとき、二次方程式\(\hspace{1pt}ax^2 + bx + c = 0\hspace{1pt}\)について以下の確率を求めよ。
　(1) \(ax^2 + bx + c = 0\hspace{2pt}\)が重解を持つ
　(2) \(ax^2 + bx + c = 0\hspace{2pt}\)が異なる二つの実数解を持つ
　(3) \(ax^2 + bx + c = 0\hspace{2pt}\)が解を持たない
　

【未知数を含む確率の問題】
問題4 : 玉が計\(\hspace{1pt}10\hspace{1pt}\)個が入っている袋があり、袋には赤玉と白玉がそれぞれ\(\hspace{1pt}2\hspace{1pt}\)個以上入っているとする。以下の条件を満たすとき、袋の中の赤玉と白玉の数を求めよ
　(1) 同時に\(\hspace{1pt}2\hspace{1pt}\)個の玉を取り出すとき、\(2\hspace{1pt}\)個とも赤玉である確率が\(\displaystyle\hspace{2pt}\frac{7}{15}\hspace{2pt}\)以上であるとき
　(2) 同時に\(\hspace{1pt}3\hspace{1pt}\)個の玉を取り出すとき、\(3\hspace{1pt}\)個とも同じ色である確率が\(\displaystyle\hspace{2pt}\frac{1}{5}\hspace{2pt}\)であるとき

問題5 : 計\(\hspace{1pt}12\hspace{1pt}\)本のくじに、当たりと外れがそれぞれ\(\hspace{1pt}2\hspace{1pt}\)本以上あるとする。このくじから同時に\(\hspace{1pt}2\hspace{1pt}\)本を引くとする。以下の条件を満たすとき、くじに何本の当たりが入っているか求めよ。
　(1) \(2\hspace{1pt}\)本とも当たりである確率が\(\displaystyle\hspace{2pt}\frac{1}{11}\hspace{2pt}\)以下であるとき
　(2) 少なくとも\(\hspace{1pt}1\hspace{1pt}\)本は当たりである確率が\(\displaystyle\hspace{2pt}\frac{15}{22}\hspace{2pt}\)以下であるとき
　

【反復試行の確率】
問題6 : 以下の図のように三角形\(\hspace{1pt}ABC\hspace{1pt}\)の頂点に点\(\hspace{1pt}P\hspace{1pt}\)がある。
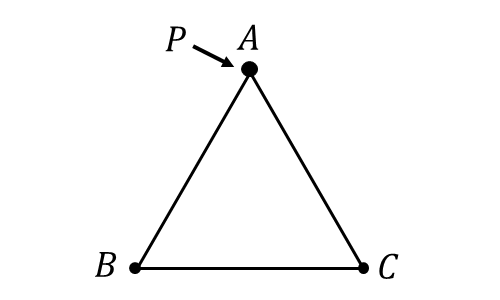
　点\(\hspace{1pt}P\hspace{1pt}\)は\(\hspace{1pt}1\hspace{1pt}\)個のサイコロを投げたときに以下のように移動する
　
　・偶数が出たとき、時計回りに次の頂点に移動する
　・\(\hspace{1pt}1, 3 \hspace{1pt}\)の目が出たとき、反時計回りに次の頂点に移動する
　・\(\hspace{1pt}5\hspace{1pt}\)の目が出たときに移動しない
　
　上記の操作を繰り返すとき、以下の確率を求めよ。
　(1) \(2\hspace{1pt}\)回の操作で点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にある確率
　(2) \(4\hspace{1pt}\)回の操作で点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にある確率
　

【トーナメント戦の確率】
問題7 : \(A , B , C , D , E , F ,G ,H\hspace{1pt}\)の\(\hspace{1pt}8\hspace{1pt}\)人が以下の図のようなトーナメント戦を行い、優勝者を決定するとする。
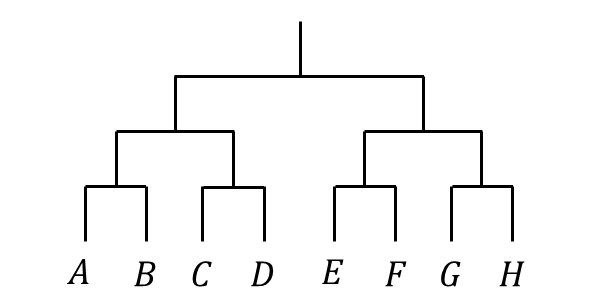
　\(A\hspace{1pt}\)が他の相手に勝つ確率を\(\hspace{1pt}p\hspace{1pt}\)\(\hspace{1pt}( 0 < p < 1)\hspace{1pt}\)とし、\(A\hspace{1pt}\)以外同士の対戦では勝敗の確率は等しいとする。また、引き分けはないとする。
　
　このとき、以下の値を求めよ
　　(1) \(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回戦目で負ける確率
　　(2) \(B\hspace{1pt}\)が優勝する確率
　　(3) \(D\hspace{1pt}\)が優勝する確率
　　(4) \(H\hspace{1pt}\)が優勝する確率