最短経路を通る道順の数を求める問題
◆第問目!
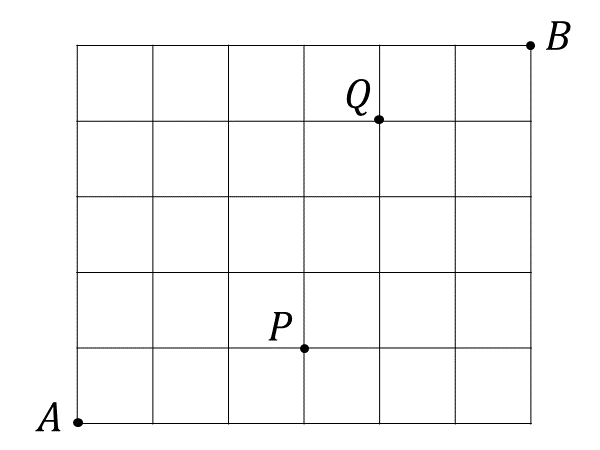
以下のような方法で地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)まで最短経路で行く道順の数を求めよ
(1) 全ての道を使う
(2) 地点\(\hspace{1pt}P\hspace{1pt}\)を通る
(3) 地点\(\hspace{1pt}P\hspace{1pt}\)を通らない
(4) 地点\(\hspace{1pt}P\hspace{1pt}\)と地点\(\hspace{1pt}Q\hspace{1pt}\)を通る
最短経路を移動する問題では、右方向に進むことを『→』、上に進むことを『↑』の記号で表し、二つの記号の順列を考えることで総数を求めます。
例えば、右に\(\hspace{1pt}2\hspace{1pt}\)回、上に\(\hspace{1pt}3\hspace{1pt}\)回移動する道順を考えるときは
$${\rightarrow \rightarrow \uparrow \uparrow \uparrow}$$
$${\rightarrow \uparrow \rightarrow \uparrow \uparrow}$$
$${ \uparrow \rightarrow \rightarrow \uparrow \uparrow}$$
$${ \cdots \cdots \cdots}$$
などと\(\hspace{1pt}2\hspace{1pt}\)本の『→』と\(\hspace{1pt}3\hspace{1pt}\)本の『↑』の順列の数から、道順の数を求められます。
この順列の総数は、『同じものを含む順列の公式』から求められます。
異なる\({\hspace{1pt}n\hspace{2pt}}\)個のものから\({\hspace{1pt}p\hspace{2pt}}\)個の同じもの、別の種類の\({\hspace{1pt}q\hspace{2pt}}\)個の同じもの、別の種類の\({\hspace{1pt}r\hspace{2pt}}\)個の同じもの\({\hspace{1pt}\cdots\hspace{2pt}}\)を取り出して並べる並べ方の総数は以下の式で表されます。
$$ \displaystyle{\frac{n\hspace{1pt}!}{p\hspace{1pt}!\hspace{1pt}q\hspace{1pt}!\hspace{1pt}r\hspace{1pt}!\cdots}}$$ ただし、\({\hspace{1pt}p+q+r+\cdots = n\hspace{1pt}}\)
地点\(\hspace{1pt}P\hspace{1pt}\)を通る道順を求めるためには、地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}P\hspace{1pt}\)の道順の数と、地点\(\hspace{1pt}P\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)の道順の数をかけることで求めます。
地点\(\hspace{1pt}P\hspace{1pt}\)を通らない道順を求めるには、余事象を考えることで簡単に計算できます。
地点\(\hspace{1pt}P\hspace{1pt}\)を通らないことの余事象は、『地点\(\hspace{1pt}P\hspace{1pt}\)を通る』となります。
地点\(\hspace{1pt}P\hspace{1pt}\)と地点\(\hspace{1pt}Q\hspace{1pt}\)を通る道順の数を求める場合、地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}P\)、地点\(\hspace{1pt}P\hspace{1pt}\)から地点\(\hspace{1pt}Q\)、地点\(\hspace{1pt}Q\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)の道順の数をかけることで求めます。
【答え】
(1) \(\hspace{1pt}462\hspace{1pt}\)通り
(2) \(\hspace{1pt}140\hspace{1pt}\)通り
(3) \(\hspace{1pt}322\hspace{1pt}\)通り
(4) \(\hspace{1pt}48\hspace{1pt}\)通り
【(1)の解答】
問題 :『地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)まで最短経路で行くとき、全ての道を使う道順の数を求めよ』

最短経路を移動する問題では、右方向に進むことを『→』、上に進むことを『↑』の記号で表し、二つの記号の順列を考えることで総数を求めます。
問題(1)は右に\(\hspace{1pt}6\hspace{1pt}\)回、上に\(\hspace{1pt}5\hspace{1pt}\)回移動すると最短経路となるため、『→』を\(\hspace{1pt}6\hspace{1pt}\)個と『↑』を\(\hspace{1pt}5\hspace{1pt}\)個の順列の総数を求めます。
同じものを含む順列の公式から $${ \frac{11!}{6! 5! } = 462}$$
すなわち、\(462\hspace{1pt}\)通りとなります。
【(2)の解答】
問題 :『地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)まで最短経路で行くとき、地点\(\hspace{1pt}P\hspace{1pt}\)を通る道順の数を求めよ』

地点\(\hspace{1pt}P\hspace{1pt}\)を通る道順の数を求める場合、地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}P\hspace{1pt}\)の道順の数と、地点\(\hspace{1pt}P\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)の道順の数をかけることで求めます。
地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}P\hspace{1pt}\)の道順の数は、『→』を\(\hspace{1pt}3\hspace{1pt}\)個と『↑』を\(\hspace{1pt}1\hspace{1pt}\)個の順列の総数を求めます。
同じものを含む順列の公式から $${ \frac{4!}{3! 1! } = 4}$$
すなわち、\(4\hspace{1pt}\)通りとなります。
また、地点\(\hspace{1pt}P\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)の道順の数は、『→』を\(\hspace{1pt}3\hspace{1pt}\)個と『↑』を\(\hspace{1pt}4\hspace{1pt}\)個の順列の総数を求めます。
同じものを含む順列の公式から $${ \frac{7!}{3! 4! } = 35}$$
すなわち、\(35\hspace{1pt}\)通りとなります。
以上から、地点\(\hspace{1pt}P\hspace{1pt}\)を通る道順の数は
$${4 \times 35 = 140}$$
であることから、\(\hspace{1pt}140\hspace{1pt}\)通りとなります。
【(3)の解答】
問題 :『地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)まで最短経路で行くとき、地点\(\hspace{1pt}P\hspace{1pt}\)を通らない道順の数を求めよ』

地点\(\hspace{1pt}P\hspace{1pt}\)を通らない道順の余事象は『地点\(\hspace{1pt}P\hspace{1pt}\)を通る』となります。
すなわち、地点\(\hspace{1pt}P\hspace{1pt}\)を通らない道順の数は『全体の道順の数』から『地点\(\hspace{1pt}P\hspace{1pt}\)を通る数』を引くことで求められます。
したがって
$${462 - 140 = 322}$$
であることから、地点\(\hspace{1pt}P\hspace{1pt}\)を通らない道順の数は\(\hspace{1pt}322\hspace{1pt}\)通りとなります。
【(4)の解答】
問題 :『地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)まで最短経路で行くとき、地点\(\hspace{1pt}P\hspace{1pt}\)と地点\(\hspace{1pt}Q\hspace{1pt}\)を通る道順の数を求めよ』

地点\(\hspace{1pt}P\hspace{1pt}\)と地点\(\hspace{1pt}Q\hspace{1pt}\)を通る道順の数を求める場合、地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}P\)、地点\(\hspace{1pt}P\hspace{1pt}\)から地点\(\hspace{1pt}Q\)、地点\(\hspace{1pt}Q\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)の道順の数をかけることで求めます。
地点\(\hspace{1pt}A\hspace{1pt}\)から地点\(\hspace{1pt}P\hspace{1pt}\)の道順の数は、『→』を\(\hspace{1pt}3\hspace{1pt}\)個と『↑』を\(\hspace{1pt}1\hspace{1pt}\)個の順列の総数を求めます。
同じものを含む順列の公式から $${ \frac{4!}{3! 1! } = 4}$$
すなわち、\(4\hspace{1pt}\)通りとなります。
また、地点\(\hspace{1pt}P\hspace{1pt}\)から地点\(\hspace{1pt}Q\hspace{1pt}\)の道順の数は、『→』を\(\hspace{1pt}1\hspace{1pt}\)個と『↑』を\(\hspace{1pt}3\hspace{1pt}\)個の順列の総数を求めます。
同じものを含む順列の公式から $${ \frac{4!}{1! 3! } = 4}$$
すなわち、\(4\hspace{1pt}\)通りとなります。
また、地点\(\hspace{1pt}Q\hspace{1pt}\)から地点\(\hspace{1pt}B\hspace{1pt}\)の道順の数は、『→』を\(\hspace{1pt}2\hspace{1pt}\)個と『↑』を\(\hspace{1pt}1\hspace{1pt}\)個の順列の総数を求めます。
同じものを含む順列の公式から $${ \frac{3!}{2! 1! } = 3}$$
すなわち、\(3\hspace{1pt}\)通りとなります。
以上から、地点\(\hspace{1pt}P\hspace{1pt}\)と地点\(\hspace{1pt}Q\hspace{1pt}\)を通る道順の数は
$${4 \times 4 \times 3 = 48}$$
であることから、\(\hspace{1pt}48\hspace{1pt}\)通りとなります。
【関連するページ】
・同じものを含む順列