トーナメントの確率の問題
◆第問目!
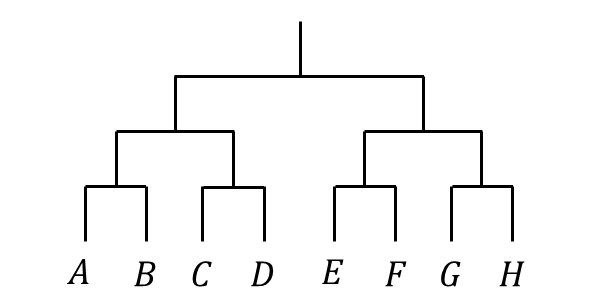
\(A\hspace{1pt}\)が他の相手に勝つ確率を\(\hspace{1pt}p\hspace{1pt}\)\(\hspace{1pt}( 0 < p < 1)\hspace{1pt}\)とし、\(A\hspace{1pt}\)以外同士の対戦では勝敗の確率は等しいとする。また、引き分けはないとする。
このとき、以下の値を求めよ
(1) \(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回戦目で負ける確率
(2) \(B\hspace{1pt}\)が優勝する確率
(3) \(D\hspace{1pt}\)が優勝する確率
(4) \(H\hspace{1pt}\)が優勝する確率
\(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回戦目で負ける確率は
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ
・\(\hspace{1pt}2\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ
・\(\hspace{1pt}3\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が負ける
という\(\hspace{1pt}3\hspace{1pt}\)つの事象が同時に起こる確率から求められます。
\(B\hspace{1pt}\)が優勝する確率は
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
・\(\hspace{1pt}2\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
・\(\hspace{1pt}3\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
という\(\hspace{1pt}3\hspace{1pt}\)つの事象が同時に起こる確率から求められます。
『\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ場合』と『\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ場合』では、\(\hspace{1pt}D\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回戦目で勝つ確率が変わります。
そのため、\(\hspace{1pt}1\hspace{1pt}\)回戦目の結果から以下のように場合分けをします。
[1] \(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ
[2] \(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
これまでの計算結果から、\(A , B , C , D\hspace{1pt}\)のいずれかが優勝する確率は、ただちに求めることができます。
『\(\hspace{1pt}A , B , C , D\hspace{1pt}\)のいずれかが優勝する』ことの余事象が、『\(\hspace{1pt}E , F , G , H\hspace{1pt}\)のいずれかが優勝する』ことであることを利用し、\(H\hspace{1pt}\)が優勝する確率を求まます。
【答え】
(1) \(\displaystyle p^2(1-p) \hspace{1pt}\)
(2) \(\displaystyle \frac{1}{4}(1-p) \hspace{1pt}\)
(3) \(\displaystyle \frac{1}{8} (1-p)(2p+1)\hspace{1pt}\)
(4) \(\displaystyle \frac{1}{8} ( 1- 2p^3 + p^2)\hspace{1pt}\)
【(1)の解答】
問題 :『\(A , B , C , D , E , F ,G ,H\hspace{1pt}\)の\(\hspace{1pt}8\hspace{1pt}\)人が以下の図のようなトーナメント戦を行い、優勝者を決定するとする。

\(A\hspace{1pt}\)が他の相手に勝つ確率を\(\hspace{1pt}p\hspace{1pt}\)\(\hspace{1pt}( 0 < p < 1)\hspace{1pt}\)とし、\(A\hspace{1pt}\)以外同士の対戦では勝敗の確率は等しいとする。また、引き分けはないとする。
このとき、\(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回戦目で負ける確率を求めよ』
\(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回戦目で負ける確率は
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ
・\(\hspace{1pt}2\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ
・\(\hspace{1pt}3\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が負ける
という\(\hspace{1pt}3\hspace{1pt}\)つの事象が同時に起こる確率を求めればよいことになります。
すなわち、\(A\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回戦目で負ける確率は
$$
\begin{aligned}
& p \times p \times (1-p) \\[0.7em]
& = p^2(1-p)\\[0.7em]
\end{aligned}
$$
と求められます。
【(2)の解答】
問題 :『\(A , B , C , D , E , F ,G ,H\hspace{1pt}\)の\(\hspace{1pt}8\hspace{1pt}\)人が以下の図のようなトーナメント戦を行い、優勝者を決定するとする。

\(A\hspace{1pt}\)が他の相手に勝つ確率を\(\hspace{1pt}p\hspace{1pt}\)\(\hspace{1pt}( 0 < p < 1)\hspace{1pt}\)とし、\(A\hspace{1pt}\)以外同士の対戦では勝敗の確率は等しいとする。また、引き分けはないとする。
このとき、\(B\hspace{1pt}\)が優勝する確率を求めよ』
\(B\hspace{1pt}\)が優勝する確率は
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
・\(\hspace{1pt}2\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
・\(\hspace{1pt}3\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
という\(\hspace{1pt}3\hspace{1pt}\)つの事象が同時に起こる確率を求めればよいことになります。
すなわち、\(B\hspace{1pt}\)が優勝する確率は
$$
\begin{aligned}
& (1-p) \times \frac{1}{2} \times \frac{1}{2} \\[0.7em]
& = \frac{1}{4}(1-p)\\[0.7em]
\end{aligned}
$$
と求められます。
【(3)の解答】
問題 :『\(A , B , C , D , E , F ,G ,H\hspace{1pt}\)の\(\hspace{1pt}8\hspace{1pt}\)人が以下の図のようなトーナメント戦を行い、優勝者を決定するとする。

\(A\hspace{1pt}\)が他の相手に勝つ確率を\(\hspace{1pt}p\hspace{1pt}\)\(\hspace{1pt}( 0 < p < 1)\hspace{1pt}\)とし、\(A\hspace{1pt}\)以外同士の対戦では勝敗の確率は等しいとする。また、引き分けはないとする。
このとき、\(D\hspace{1pt}\)が優勝する確率を求めよ』
『\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ場合』と『\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ場合』では、\(\hspace{1pt}D\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回戦目で勝つ確率が変わります。
そのため、\(\hspace{1pt}1\hspace{1pt}\)回戦目の結果から以下のように場合分けをします。
[1] \(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ
[2] \(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ
[1],[2]のそれぞれの場合について\(\hspace{1pt}D\hspace{1pt}\)が優勝する確率を求めます。
[1] \(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つ場合
\(D\hspace{1pt}\)が優勝する確率は
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が\(\hspace{1pt}B\hspace{1pt}\)に勝つ
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}D\hspace{1pt}\)が\(\hspace{1pt}C\hspace{1pt}\)に勝つ
・\(\hspace{1pt}2\hspace{1pt}\)回戦目で\(\hspace{1pt}D\hspace{1pt}\)が\(\hspace{1pt}A\hspace{1pt}\)に勝つ
・\(\hspace{1pt}3\hspace{1pt}\)回戦目で勝つ
という\(\hspace{1pt}4\hspace{1pt}\)つの事象が同時に起こる確率を求めればよいことになります。
よって、\(D\hspace{1pt}\)が優勝する確率は $$ \begin{aligned} & p \times \frac{1}{2} \times (1-p) \times \frac{1}{2} \\[0.7em] & = \frac{1}{4}p(1-p)\\[0.7em] \end{aligned} $$ となります。
[2] \(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が勝つ場合
\(D\hspace{1pt}\)が優勝する確率は
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}B\hspace{1pt}\)が\(\hspace{1pt}A\hspace{1pt}\)に勝つ
・\(\hspace{1pt}1\hspace{1pt}\)回戦目で\(\hspace{1pt}D\hspace{1pt}\)が\(\hspace{1pt}C\hspace{1pt}\)に勝つ
・\(\hspace{1pt}2\hspace{1pt}\)回戦目で\(\hspace{1pt}D\hspace{1pt}\)が\(\hspace{1pt}B\hspace{1pt}\)に勝つ
・\(\hspace{1pt}3\hspace{1pt}\)回戦目で勝つ
という\(\hspace{1pt}4\hspace{1pt}\)つの事象が同時に起こる確率を求めればよいことになります。
よって、\(D\hspace{1pt}\)が優勝する確率は $$ \begin{aligned} & (1-p) \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \\[0.7em] & = \frac{1}{8}(1-p)\\[0.7em] \end{aligned} $$ となります。
すなわち、[1]と[2]は互いに排反であるから、求める確率は
$$
\begin{aligned}
& \frac{1}{4}p(1-p) + \frac{1}{8}(1-p) \\[0.7em]
& = \frac{1}{8} (1-p)(2p+1)\\[0.7em]
\end{aligned}
$$
と求められます。
【(4)の解答】
問題 :『\(A , B , C , D , E , F ,G ,H\hspace{1pt}\)の\(\hspace{1pt}8\hspace{1pt}\)人が以下の図のようなトーナメント戦を行い、優勝者を決定するとする。

\(A\hspace{1pt}\)が他の相手に勝つ確率を\(\hspace{1pt}p\hspace{1pt}\)\(\hspace{1pt}( 0 < p < 1)\hspace{1pt}\)とし、\(A\hspace{1pt}\)以外同士の対戦では勝敗の確率は等しいとする。また、引き分けはないとする。
このとき、\(H\hspace{1pt}\)が優勝する確率を求めよ』
まず\(\hspace{1pt}A , B , C , D\hspace{1pt}\)のいずれかが優勝する確率を求めます。
\(\hspace{1pt}A\hspace{1pt}\)が優勝する確率は\(\displaystyle\hspace{1pt}p^3\hspace{1pt}\)となります。
\(B\hspace{1pt}\)が優勝する確率は問題(2)から\(\displaystyle\hspace{1pt}\frac{1}{4}(1-p)\hspace{1pt}\)となります。
\(C , D\hspace{1pt}\)が優勝する確率は等しいため、\(C \hspace{1pt}\)または\(\hspace{1pt}D\hspace{1pt}\)が優勝する確率は問題(3)から $$ \begin{aligned} & \frac{1}{8} (1-p)(2p+1) \times 2 \\[0.7em] & = \frac{1}{4} (1-p)(2p+1)\\[0.7em] \end{aligned} $$ となります。
つまり、\(A , B , C , D\hspace{1pt}\)のいずれかが優勝する確率は
となります。
ここで、\(A , B , C , D\hspace{1pt}\)のいずれかが優勝することの余事象は、\(E , F , G , H\hspace{1pt}\)のいずれかが優勝することとなります。
\(\hspace{1pt}E , F , G , H\hspace{1pt}\)の\(\hspace{1pt}4\hspace{1pt}\)人は優勝する確率が等しいため、\(\hspace{1pt}H\hspace{1pt}\)の優勝する確率は以下のように求められます。
となります。
【入試本番に向けたアドバイス】
トーナメント戦の問題を解くポイントは、『勝ち上がる人が変わると、勝敗の確率が変化するかどうか』に着目するところにあります。
例えば、本問のように\(\hspace{1pt}A , B , C , D , E , F ,G ,H\hspace{1pt}\)の\(\hspace{1pt}8\hspace{1pt}\)人が出場するトーナメントで、\(\hspace{1pt}A\hspace{1pt}\)のみが勝つ確率が高く、他の選手同士の勝敗の確率は等しいとします。

このとき、\(A\hspace{1pt}\)が優勝する確率を求める場合、\(A\hspace{1pt}\)はどの選手に対しても勝つ確率が一定であるため、\(A\hspace{1pt}\)以外の誰が勝ち上がるかは考慮する必要がありません。
一方、\(C\hspace{1pt}\)や\(\hspace{1pt}D\hspace{1pt}\)が優勝する確率を求める場合、\(1\hspace{1pt}\)回戦目で\(\hspace{1pt}A\hspace{1pt}\)が勝つか\(\hspace{1pt}B\hspace{1pt}\)が勝つかで、\(2\hspace{1pt}\)回戦目に勝つ確率が変化するため、場合分けが必要になります。
さらに、\(E , F , G ,H\hspace{1pt}\)が優勝する確率を求める場合、\(3\hspace{1pt}\)回戦目の対戦相手が\(\hspace{1pt}A\hspace{1pt}\)か\(\hspace{1pt}B\hspace{1pt}\)か\(\hspace{1pt}C\hspace{1pt}\)か\(\hspace{1pt}D\hspace{1pt}\)のそれぞれについて考える必要があるため、計算が多くなります。
そこで、本問の解答では問題(2),(3)の結果を利用し、余事象から確率を求めています。
【関連するページ】
・余事象の確率