三角形の頂点を移動する点の確率
◆第問目!
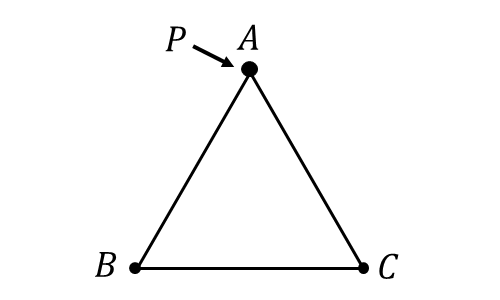
点\(\hspace{1pt}P\hspace{1pt}\)は\(\hspace{1pt}1\hspace{1pt}\)個のサイコロを投げたときに以下のように移動する
・偶数が出たとき、時計回りに次の頂点に移動する
・\(\hspace{1pt}1, 3 \hspace{1pt}\)の目が出たとき、反時計回りに次の頂点に移動する
・\(\hspace{1pt}5\hspace{1pt}\)の目が出たときに移動しない
上記の操作を繰り返すとき、以下の確率を求めよ。
(1) \(2\hspace{1pt}\)回の操作で点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にある確率
(2) \(4\hspace{1pt}\)回の操作で点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にある確率
\(\hspace{1pt}3\hspace{1pt}\)つの事象をそれぞれ\(\hspace{1pt}X,Y,Z\hspace{1pt}\)とします。
・\(\hspace{1pt}X\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が時計回りに次の頂点に移動する
・\(\hspace{1pt}Y\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が反時計回りに次の頂点に移動する
・\(\hspace{1pt}Z\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が移動しない
\(\hspace{1pt}2\hspace{1pt}\)回操作を繰り返すとき、点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にあるためには
・事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回
・事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回
のどちらかとなります。
『事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回が起こる確率』は反復試行の確率と同じ考え方で求めることができます。
事象\({\hspace{1pt}X\hspace{1pt}}\)が起こることを『\(\hspace{1pt}X\hspace{1pt}\)』、事象\({\hspace{1pt}Y\hspace{1pt}}\)が起こることを『\({\hspace{1pt}Y\hspace{1pt}}\)』として、\({\hspace{1pt}X\hspace{2pt}}\)が\({\hspace{1pt}1\hspace{2pt}}\)回、\({\hspace{1pt}Y\hspace{2pt}}\)が\({\hspace{1pt}1\hspace{2pt}}\)回起こる全ての事象の数を数えます。
| \({1\hspace{2pt}}\)回目 | \({2\hspace{2pt}}\)回目 |
|---|---|
| \(\hspace{1pt}X\hspace{1pt}\) | \(\hspace{1pt}Y\hspace{1pt}\) |
| \(\hspace{1pt}Y\hspace{1pt}\) | \(\hspace{1pt}X\hspace{1pt}\) |
上記の表のように\({2\hspace{2pt}}\)回の操作から\({\hspace{1pt}1\hspace{2pt}}\)回の『\(\hspace{1pt}X\hspace{1pt}\)』が発生する操作を選ぶと考えると、その総数は\({\hspace{1pt}{}_2 C_1=2\hspace{2pt}}\)となります。
事象\(\hspace{1pt}X\hspace{1pt}\)、事象\(\hspace{1pt}Y\hspace{1pt}\)が起こる確率は、それぞれの操作が独立であることから $${{}_2 C_1 \left( \frac{1}{2} \times \frac{1}{3}\right)}$$ と求められます。
\(\hspace{1pt}3\hspace{1pt}\)つの事象をそれぞれ\(\hspace{1pt}X,Y,Z\hspace{1pt}\)とします。
・\(\hspace{1pt}X\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が時計回りに次の頂点に移動する
・\(\hspace{1pt}Y\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が反時計回りに次の頂点に移動する
・\(\hspace{1pt}Z\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が移動しない
\(\hspace{1pt}4\hspace{1pt}\)回操作を繰り返すとき、点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にあるためには
・[1] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回
・[2] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回
・[3] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回
・[4] 事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回
・[5] 事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}4\hspace{1pt}\)回
のいずれかとなります。
[3]の『事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回起こる確率』は反復試行の確率と同じ考え方で求めることができます。
事象\({\hspace{1pt}X\hspace{1pt}}\)が起こることを『\(\hspace{1pt}X\hspace{1pt}\)』、事象\({\hspace{1pt}Y\hspace{1pt}}\)が起こることを『\({\hspace{1pt}Y\hspace{1pt}}\)』、事象\({\hspace{1pt}Z\hspace{1pt}}\)が起こることを『\({\hspace{1pt}Z\hspace{1pt}}\)』として、\({\hspace{1pt}X\hspace{2pt}}\)が\({\hspace{1pt}1\hspace{2pt}}\)回、\({\hspace{1pt}Y\hspace{2pt}}\)が\({\hspace{1pt}1\hspace{2pt}}\)回、\({\hspace{1pt}Z\hspace{2pt}}\)が\({\hspace{1pt}2\hspace{2pt}}\)回起こる全ての事象の数を数えます。
| \({1\hspace{2pt}}\)回目 | \({2\hspace{2pt}}\)回目 | \({3\hspace{2pt}}\)回目 | \({4\hspace{2pt}}\)回目 |
|---|---|---|---|
| \(\hspace{1pt}X\hspace{1pt}\) | \(\hspace{1pt}Y\hspace{1pt}\) | \(\hspace{1pt}Z\hspace{1pt}\) | \(\hspace{1pt}Z\hspace{1pt}\) |
| \(\hspace{1pt}X\hspace{1pt}\) | \(\hspace{1pt}Z\hspace{1pt}\) | \(\hspace{1pt}Y\hspace{1pt}\) | \(\hspace{1pt}Z\hspace{1pt}\) |
| \(\hspace{1pt}\cdots\hspace{1pt}\) | \(\hspace{1pt}\cdots\hspace{1pt}\) | \(\hspace{1pt}\cdots\hspace{1pt}\) | \(\hspace{1pt}\cdots\hspace{1pt}\) |
| \(\hspace{1pt}Z\hspace{1pt}\) | \(\hspace{1pt}Z\hspace{1pt}\) | \(\hspace{1pt}Y\hspace{1pt}\) | \(\hspace{1pt}X\hspace{1pt}\) |
上記の表のように\({4\hspace{2pt}}\)回の操作から\({\hspace{1pt}1\hspace{2pt}}\)回の『\(\hspace{1pt}X\hspace{1pt}\)』、\({1\hspace{2pt}}\)回の『\(\hspace{1pt}Y\hspace{1pt}\)』、\({2\hspace{2pt}}\)回の『\(\hspace{1pt}Z\hspace{1pt}\)』が発生する操作を選ぶと考えると、その総数は\({\displaystyle\hspace{1pt}{}_4 C_1 \cdot {}_3 C_1 \cdot {}_2 C_2 =12\hspace{2pt}}\)通りとなります。
事象\(\hspace{1pt}X\hspace{1pt}\)、事象\(\hspace{1pt}Y\hspace{1pt}\)、事象\(\hspace{1pt}Z\hspace{1pt}\)が起こる確率は、それぞれの操作が独立であることから $${{}_4 C_1 \cdot {}_3 C_1\cdot \frac{1}{2} \cdot \frac{1}{3} \cdot \left( \frac{1}{6}\right)^2}$$ と求められます。
【答え】
(1) \(\displaystyle\frac{13}{36}\hspace{1pt}\)
(2) \(\displaystyle \frac{143}{432}\hspace{1pt}\)
【(1)の解答】
問題 :『以下の図のように三角形\(\hspace{1pt}ABC\hspace{1pt}\)の頂点に点\(\hspace{1pt}P\hspace{1pt}\)がある。

点\(\hspace{1pt}P\hspace{1pt}\)は\(\hspace{1pt}1\hspace{1pt}\)個のサイコロを投げたときに以下のように移動する
・偶数が出たとき、時計回りに次の頂点に移動する
・\(\hspace{1pt}1, 3 \hspace{1pt}\)の目が出たとき、反時計回りに次の頂点に移動する
・\(\hspace{1pt}5\hspace{1pt}\)の目が出たときに移動しない
上記の操作を\(\hspace{1pt}2\hspace{1pt}\)回繰り返すとき、点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にある確率を求めよ』
\(\hspace{1pt}3\hspace{1pt}\)つの事象をそれぞれ\(\hspace{1pt}X,Y,Z\hspace{1pt}\)とします。
・\(\hspace{1pt}X\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が時計回りに次の頂点に移動する
・\(\hspace{1pt}Y\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が反時計回りに次の頂点に移動する
・\(\hspace{1pt}Z\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が移動しない
このとき、事象\(\hspace{1pt}X,Y,Z\hspace{1pt}\)の起こる確率は $$ \begin{aligned} & P(X) = \frac{1}{2}\\[0.7em] & \hspace{1pt}P(Y) = \frac{1}{3} \\[0.7em] & \hspace{1pt}P(Z) = \frac{1}{6} \\[0.7em] \end{aligned} $$ となります。
\(\hspace{1pt}2\hspace{1pt}\)回操作を繰り返すとき、点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にあるためには
・事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回
・事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回
のどちらかとなります。
したがって、上記の事象は互いに排反であることから、求める確率は
$$
\begin{aligned}
& {}_2 C_1 \left( \frac{1}{2} \cdot \frac{1}{3}\right) + \frac{1}{6}\cdot \frac{1}{6}\\[0.7em]
& = \frac{1}{3} + \frac{1}{36} \\[0.7em]
& = \frac{13}{36} \\[0.7em]
\end{aligned}
$$
となります。
【(2)の解答】
問題 :『以下の図のように三角形\(\hspace{1pt}ABC\hspace{1pt}\)の頂点に点\(\hspace{1pt}P\hspace{1pt}\)がある。

点\(\hspace{1pt}P\hspace{1pt}\)は\(\hspace{1pt}1\hspace{1pt}\)個のサイコロを投げたときに以下のように移動する
・偶数が出たとき、時計回りに次の頂点に移動する
・\(\hspace{1pt}1, 3 \hspace{1pt}\)の目が出たとき、反時計回りに次の頂点に移動する
・\(\hspace{1pt}5\hspace{1pt}\)の目が出たときに移動しない
上記の操作を\(\hspace{1pt}4\hspace{1pt}\)回繰り返すとき、点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にある確率を求めよ』
問題(1)と同様に、\(\hspace{1pt}3\hspace{1pt}\)つの事象をそれぞれ\(\hspace{1pt}X,Y,Z\hspace{1pt}\)とします。
・\(\hspace{1pt}X\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が時計回りに次の頂点に移動する
・\(\hspace{1pt}Y\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が反時計回りに次の頂点に移動する
・\(\hspace{1pt}Z\hspace{1pt}\) : 点\(\hspace{1pt}P\hspace{1pt}\)が移動しない
このとき、事象\(\hspace{1pt}X,Y,Z\hspace{1pt}\)の起こる確率は $$ \begin{aligned} & P(X) = \frac{1}{2}\\[0.7em] & \hspace{1pt}P(Y) = \frac{1}{3} \\[0.7em] & \hspace{1pt}P(Z) = \frac{1}{6} \\[0.7em] \end{aligned} $$ となります。
\(\hspace{1pt}4\hspace{1pt}\)回操作を繰り返すとき、点\(\hspace{1pt}P\hspace{1pt}\)が点\(\hspace{1pt}A\hspace{1pt}\)にあるためには
・[1] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回
・[2] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回
・[3] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回
・[4] 事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回
・[5] 事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}4\hspace{1pt}\)回
のいずれかとなります。
・[1] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回起こる確率
\({4\hspace{2pt}}\)回の操作のうち、事象\(\hspace{1pt}X\hspace{1pt}\)が\({\hspace{1pt}3\hspace{1pt}}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\({\hspace{1pt}1\hspace{2pt}}\)回起こる場合の数は\({\displaystyle\hspace{1pt}{}_4 C_3 =4\hspace{2pt}}\)通りとなることから
$${{}_4 C_3 \left( \frac{1}{2}\right)^3 \cdot \frac{1}{6} = \frac{1}{12}}$$
となります。
・[2] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回起こる確率
\({4\hspace{2pt}}\)回の操作のうち、事象\(\hspace{1pt}X\hspace{1pt}\)が\({\hspace{1pt}2\hspace{1pt}}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\({\hspace{1pt}2\hspace{2pt}}\)回起こる場合の数は\({\displaystyle\hspace{1pt}{}_4 C_2 =6\hspace{2pt}}\)通りとなることから
$${{}_4 C_2 \left( \frac{1}{2}\right)^2 \cdot \left( \frac{1}{3}\right)^2 = \frac{1}{6}}$$
となります。
・[3] 事象\(\hspace{1pt}X\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)回起こる確率
\({4\hspace{2pt}}\)回の操作のうち、事象\(\hspace{1pt}X\hspace{1pt}\)が\({\hspace{1pt}1\hspace{1pt}}\)回、事象\(\hspace{1pt}Y\hspace{1pt}\)が\({\hspace{1pt}1\hspace{2pt}}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\({\hspace{1pt}2\hspace{2pt}}\)回起こる場合の数は\({\displaystyle\hspace{1pt}{}_4 C_1 \times {}_3 C_1 =12\hspace{2pt}}\)通りとなることから
$${{}_4 C_1 \cdot {}_3 C_1 \cdot \frac{1}{2} \cdot \frac{1}{3} \cdot \left( \frac{1}{6}\right)^2 = \frac{1}{18}}$$
となります。
・[4] 事象\(\hspace{1pt}Y\hspace{1pt}\)が\(\hspace{1pt}3\hspace{1pt}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}1\hspace{1pt}\)回起こる確率
\({4\hspace{2pt}}\)回の操作のうち、事象\(\hspace{1pt}Y\hspace{1pt}\)が\({\hspace{1pt}3\hspace{2pt}}\)回、事象\(\hspace{1pt}Z\hspace{1pt}\)が\({\hspace{1pt}1\hspace{2pt}}\)回起こる場合の数は\({\displaystyle\hspace{1pt}{}_4 C_3 =4\hspace{2pt}}\)通りとなることから
$${{}_4 C_3 \cdot \left( \frac{1}{3}\right)^3 \cdot \frac{1}{6} = \frac{2}{81}}$$
となります。
・[5] 事象\(\hspace{1pt}Z\hspace{1pt}\)が\(\hspace{1pt}4\hspace{1pt}\)回起こる確率
\({4\hspace{2pt}}\)回の操作のうち、事象\(\hspace{1pt}Z\hspace{1pt}\)が\({\hspace{1pt}4\hspace{2pt}}\)回起こる場合の数は\({\displaystyle\hspace{1pt}{}_4 C_4 =1\hspace{2pt}}\)通りとなることから
$${\left( \frac{1}{6}\right)^4 = \frac{1}{1296}}$$
となります。
したがって、[1]~[5]の事象は互いに排反であることから、求める確率は
と求められます。
【入試本番に向けたアドバイス】
本問は、サイコロを振った結果から点\(\hspace{1pt}P\hspace{1pt}\)が三角形の頂点を移動するとき、ある点の位置にいる確率を求める問題です。
類題として、『数直線上を動く点\(\hspace{1pt}P\hspace{1pt}\)』や『四角形の頂点を動く点\(\hspace{1pt}P\hspace{1pt}\)』、『平面の格子点(座標が整数となる点)を動く点\(\hspace{1pt}P\hspace{1pt}\)』の確率の問題などがあります。
このタイプの問題の解法としては
① ある回数の試行の後、点\(\hspace{1pt}P\hspace{1pt}\)が指定された位置にいる事象を全て書き並べる
② 反復試行の確率の考え方から、各事象の確率を求める
という解法が定石です。
【確率の計算の注意点】
高校数学の教科書で解説されている反復試行の確率の公式は、以下のような式で表されます。
\({\hspace{1pt}1\hspace{2pt}}\)回の試行により事象\({\hspace{1pt}A\hspace{2pt}}\)の起こる確率が\({\hspace{1pt}p\hspace{2pt}}\)であるとする。この試行を\({\hspace{1pt}n\hspace{1pt}}\)回繰り返して行うとき、事象\({\hspace{1pt}A\hspace{2pt}}\)が\({\hspace{1pt}r\hspace{2pt}}\)回起こる確率は $${{}_n C_r \hspace{2pt}p^{\hspace{2pt}r} \hspace{1pt} (1-p)^{n-r}}$$
上記の公式は 事象\({\hspace{1pt}A\hspace{2pt}}\)が\({\hspace{1pt}r\hspace{2pt}}\)回起こり、事象\({\hspace{1pt}\overline{A}\hspace{2pt}}\)が\({\hspace{1pt}n-r\hspace{2pt}}\)回起こる 確率を求める公式であるという点に注意が必要です。
例えば、『サイコロを振り、偶数が出たときに点\(\hspace{1pt}P\hspace{1pt}\)が三角形の頂点を時計回りに進み、奇数が出たときは反時計回りに進む』のように\(\hspace{1pt}2\hspace{1pt}\)つの事象のみの問題であれば、上記の公式からそのまま計算することができます。
一方、本問のように『サイコロを振り、偶数が出たときに点\(\hspace{1pt}P\hspace{1pt}\)が三角形の頂点を時計回りに進み、\(\hspace{1pt}1,3\hspace{1pt}\)が出たときは反時計回りに進み、\(5\hspace{1pt}\)が出たときは動かない』という\(\hspace{1pt}3\hspace{1pt}\)つの事象がある問題の場合は、公式をそのまま当てはめることができません。
ヒント(1),(2)で解説したように\(\hspace{1pt}3\hspace{1pt}\)つの事象の起こる総数を求めて計算する必要があります。
【約分の計算】
確率の問題では、本問の分数\(\displaystyle\hspace{1pt}\frac{429}{1296} \hspace{1pt}\)のように分母、分子の値が大きい分数の約分が必要になります。
\(\displaystyle\hspace{1pt}\frac{429}{1296} = \frac{429}{6^4} \hspace{1pt}\)を約分するときは、分母が\(\hspace{1pt}6^4\hspace{1pt}\)であることから、分子が\(\hspace{1pt}2\hspace{1pt}\)の倍数か\(\hspace{1pt}3\hspace{1pt}\)の倍数かを調べます。
まず、\(\hspace{1pt}429\hspace{1pt}\)の各桁の和が\(\hspace{1pt}3\hspace{1pt}\)の倍数であることから、\(\hspace{1pt}3\hspace{1pt}\)の倍数であることが分かります。
\(\hspace{1pt}429 \div 3 = 143\hspace{1pt}\)となります。ここで、\(143\hspace{1pt}\)の各桁の和は\(\hspace{1pt}3\hspace{1pt}\)の倍数ではなく、また偶数でもないため、\(\displaystyle\hspace{1pt}\frac{429}{6^4} \hspace{1pt}\)を約分した結果が\(\displaystyle\hspace{1pt}\frac{143}{432} \hspace{1pt}\)と分かります。
サイコロを用いた反復試行の確率の計算では、分母が\(\hspace{1pt}6\hspace{1pt}\)のべき乗となり大きい数となりますが、分子が\(\hspace{1pt}2\hspace{1pt}\)の倍数か\(\hspace{1pt}3\hspace{1pt}\)の倍数かだけをチェックすれば素早く計算できます。
【関連するページ】
・反復試行の確率