円周に並んだ点のうち3点を結んだ三角形の数
◆第問目!
例えば、下図は点\(\hspace{1pt}A_1 , A_4 , A_8\hspace{1pt}\)を選んだときの三角形である。
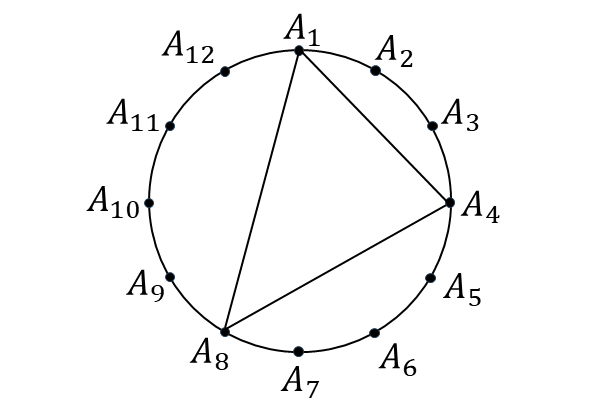
このとき、以下のような三角形が何通りできるか求めよ。
(1) 三角形の数
(2) 正三角形の数
(3) 正三角形でない二等辺三角形の数
(4) 直角三角形の数
作られる三角形の数は、円周上の\(\hspace{1pt}12\hspace{1pt}\)個の点から\(\hspace{1pt}3\hspace{1pt}\)個の点を選んだ組み合わせの数と考えることができます。
点は円周上を\(\hspace{1pt}12\hspace{1pt}\)等分していることから、点と点の間の弧の長さが等しくなるような\(\hspace{1pt}3\hspace{1pt}\)点を選ぶと、三辺が等しい長さの三角形となります。
『\(2\hspace{1pt}\)つの辺の長さが等しい』ことを『ある\(\hspace{1pt}1\hspace{1pt}\)点から弧の長さが等しい\(\hspace{1pt}2\hspace{1pt}\)つの点を選ぶ』と考えて、二等辺三角形となる点の選び方を求めます。
基準となる\(\hspace{1pt}1\hspace{1pt}\)点を定め、その\(\hspace{1pt}1\hspace{1pt}\)点からの弧の長さが等しくなる\(\hspace{1pt}2\hspace{1pt}\)点の選び方を数えます。
このとき、正三角形となる三角形を数えないように注意が必要です。
タレスの定理から、\(1\hspace{1pt}\)辺が円の直径となるように円周上の異なる\(\hspace{1pt}3\hspace{1pt}\)点を選ぶと、選ばれた点を頂点とする三角形は直角三角形となります。
【答え】
(1) \(\displaystyle\hspace{1pt} 220\hspace{1pt}\)通り
(2) \(\displaystyle\hspace{1pt} 4\hspace{1pt}\)通り
(3) \(\displaystyle\hspace{1pt} 48\hspace{1pt}\)通り
(4) \(\displaystyle\hspace{1pt} 60\hspace{1pt}\)通り
【(1)の解答】
問題 :『円周上を\(\hspace{1pt}12\hspace{1pt}\)等分する点\(\hspace{1pt}A_i\hspace{1pt}\)\(\hspace{1pt}(1 \leqq i \leqq 12)\hspace{1pt}\)がある。これらの点から異なる\(\hspace{1pt}3\hspace{1pt}\)点を選び、選ばれた点を頂点とする三角形を作るとき、三角形が何通りできるか求めよ』
問題(1)は、円周上の\(\hspace{1pt}12\hspace{1pt}\)個の点から\(\hspace{1pt}3\hspace{1pt}\)個の点を選んだ組み合わせの数と考えることができます。
すなわち $$ \begin{aligned} {}_{12} C_3 & = \frac{{}_{12} P_3}{3!}\\[0.7em] & =\frac{12 \cdot 11 \cdot 10}{3 \cdot 2 \cdot 1}\\[0.7em] & =220\\[0.7em] \end{aligned} $$ となります。
したがって、作られる三角形の数は\(\displaystyle\hspace{1pt}220\hspace{1pt}\)通りとなります。
【(2)の解答】
問題 :『円周上を\(\hspace{1pt}12\hspace{1pt}\)等分する点\(\hspace{1pt}A_i\hspace{1pt}\)\(\hspace{1pt}(1 \leqq i \leqq 12)\hspace{1pt}\)がある。これらの点から異なる\(\hspace{1pt}3\hspace{1pt}\)点を選び、選ばれた点を頂点とする三角形を作るとき、正三角形が何通りできるか求めよ』
点と点の間の弧の長さが等しくなるような\(\hspace{1pt}3\hspace{1pt}\)点を選ぶと、三辺が等しい長さの三角形となります。
まず、点\(\hspace{1pt}A_1\hspace{1pt}\)を基準とする点とします。
点\(\hspace{1pt}A_1\hspace{1pt}\)を頂点にもつ正三角形は\(\hspace{1pt}\bigtriangleup A_1 A_5 A_9\hspace{1pt}\)となります。

次に、基準とした点\(\hspace{1pt}A_1\hspace{1pt}\)を、隣りの点に回転させた点\(\hspace{1pt}A_2\hspace{1pt}\)を頂点にもつ正三角形は\(\hspace{1pt}\bigtriangleup A_2 A_6 A_{10}\hspace{1pt}\)となります。
このように基準とした点から、\(1\hspace{1pt}\)点ずつ回転させた三角形を数えると\(\hspace{2pt}\bigtriangleup A_3 A_7 A_{11}\hspace{1pt}\)と\(\bigtriangleup A_4 A_8 A_{12}\hspace{1pt}\)も正三角形であることが分かります。
さらに三角形を回転させると、すでに数えた正三角形と重複することから、求める正三角形の数は\(\hspace{1pt}4\hspace{1pt}\)通りと数えることができます。
【(3)の解答】
問題 :『円周上を\(\hspace{1pt}12\hspace{1pt}\)等分する点\(\hspace{1pt}A_i\hspace{1pt}\)\(\hspace{1pt}(1 \leqq i \leqq 12)\hspace{1pt}\)がある。これらの点から異なる\(\hspace{1pt}3\hspace{1pt}\)点を選び、選ばれた点を頂点とする三角形を作るとき、正三角形でない二等辺三角形が何通りできるか求めよ』
『\(2\hspace{1pt}\)つの辺の長さが等しい』ことを『ある\(\hspace{1pt}1\hspace{1pt}\)点から弧の長さが等しい\(\hspace{1pt}2\hspace{1pt}\)つの点を選ぶ』と考えて、二等辺三角形となる点の選び方を求めます。
まず、点\(\hspace{1pt}A_1\hspace{1pt}\)を基準とする点とします。
点\(\hspace{1pt}A_1\hspace{1pt}\)を頂点にもつ二等辺三角形は、点\(\hspace{1pt}A_1\hspace{1pt}\)からの弧の長さが等しくなる\(\hspace{1pt}2\hspace{1pt}\)点を選べばよいので、\(\bigtriangleup A_1 A_2 A_{12}\hspace{1pt}\)、\(\bigtriangleup A_1 A_3 A_{11}\hspace{1pt}\)、\(\bigtriangleup A_1 A_4 A_{10}\hspace{1pt}\)、\(\bigtriangleup A_1 A_6 A_{8}\hspace{1pt}\)の\(\hspace{1pt}4\hspace{1pt}\)通りとなります。
(本問は正三角形を除外するため、\(\hspace{2pt}\bigtriangleup A_1 A_5 A_{9}\hspace{1pt}\)を数えない点に注意が必要です。)
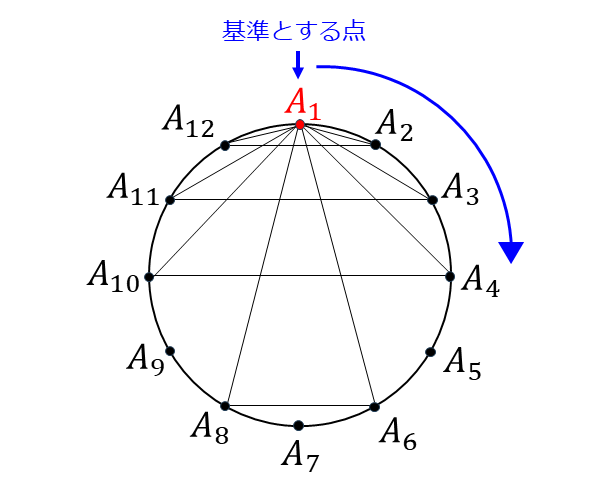
次に、基準とした点\(\hspace{1pt}A_1\hspace{1pt}\)を回転させると考えると、\(12\hspace{1pt}\)個の点に対し、それぞれ\(\hspace{1pt}4\hspace{1pt}\)通りの二等辺三角形が作られることになります。
したがって、求める二等辺三角形の数は
$${12 \times 4 = 48}$$
と求められます。
【(4)の解答】
問題 :『円周上を\(\hspace{1pt}12\hspace{1pt}\)等分する点\(\hspace{1pt}A_i\hspace{1pt}\)\(\hspace{1pt}(1 \leqq i \leqq 12)\hspace{1pt}\)がある。これらの点から異なる\(\hspace{1pt}3\hspace{1pt}\)点を選び、選ばれた点を頂点とする三角形を作るとき、直角三角形が何通りできるか求めよ』
タレスの定理から、\(1\hspace{1pt}\)辺が円の直径となるように円周上の異なる\(\hspace{1pt}3\hspace{1pt}\)点を選ぶと、選ばれた点を頂点とする三角形は直角三角形となります。
まず、点\(\hspace{1pt}A_1\hspace{1pt}\)を基準とする点とします。
このとき、点\(\hspace{1pt}A_1\hspace{1pt}\)と点\(\hspace{1pt}A_7\hspace{1pt}\)を選んだときに、一辺が円の直径となります。
他の\(\hspace{1pt}1\hspace{1pt}\)点の選び方は、下図のように\(\hspace{1pt}A_1 , A_7 \hspace{1pt}\)以外の点を選べばよいので\(\hspace{1pt}10\hspace{1pt}\)通りとなります。
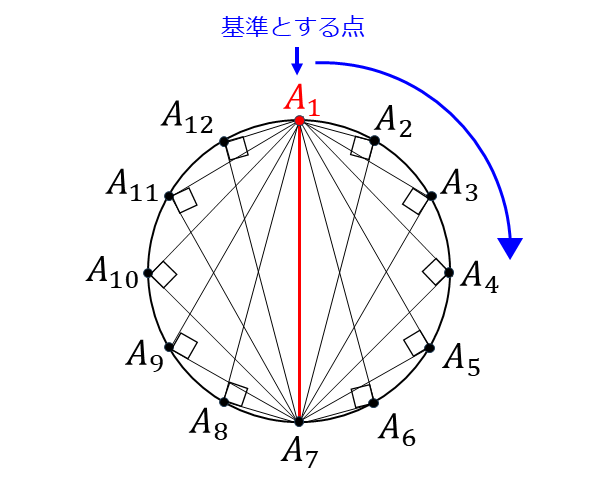
次に、基準とした点\(\hspace{1pt}A_1\hspace{1pt}\)を回転させると考えると、点\(\hspace{1pt}A_1 , A_2 , A_3 , A_4, A_5 , A_6\hspace{1pt}\)の\(\hspace{1pt}6\hspace{1pt}\)個の点に対し、それぞれ\(\hspace{1pt}10\hspace{1pt}\)通りの直角三角形が作られることになります。
(点\(\hspace{1pt}A_7 , A_8 , A_9 , A_{10}, A_{11} , A_{12}\hspace{1pt}\)は重複するため数えません。)
したがって、求める直角三角形の数は
$${10 \times 6 = 60}$$
と求められます。
【入試本番に向けたアドバイス】
円周上に等間隔にある点を結んだ図形の数を数える問題は、場合の数の範囲では頻出のテーマの一つです。
本問の類題として、『正十二角形の頂点を結んでできる図形』や『円周上を\(\hspace{1pt}9\hspace{1pt}\)等分する点を結んでできる図形』の問題などがありますが、同じ考え方で解くことができます。
本問のような円形に並んだ点を結んでできる図形の数の問題は、力技で全ての場合を数えようとすると、数え漏れや重複が発生しがちです。
そこで、まず基準となる点を決めて、その点において条件を満たす図形の数を数えます。
次に、その点を回転させて全体の数を数えるようにします。
【関連するページ】
・組み合わせの公式