ベクトルによる三角形の面積の公式

本項では以下の内容を解説します。

• ・ベクトルによる三角形の面積の公式
• ・公式の証明
• ・計算問題

1. 三角形の面積の公式

ベクトルにより三角形の面積を求める公式について解説します。

以下のような三角形\(OAB\hspace{2pt}\)において\(\hspace{1pt}\overrightarrow{OA} = \vec{a}\hspace{2pt},\hspace{2pt}\overrightarrow{OB} = \vec{b}\hspace{2pt}\)とします。

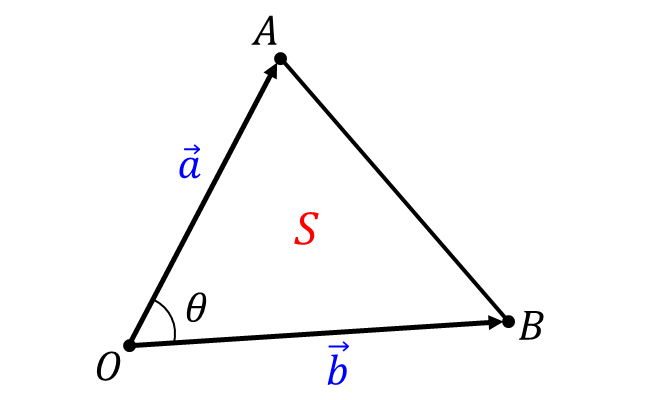
この三角形\(OAB\hspace{2pt}\)の面積\(\hspace{1pt}S\hspace{2pt}\)は以下の公式によって求められます。

また、上記の公式を成分表示すると、\(3\hspace{2pt}\)点\(\hspace{1pt}O(0\hspace{1pt},\hspace{1pt}0)\hspace{2pt},\)\(\hspace{3pt}A(a_1\hspace{1pt},\hspace{1pt}a_2)\hspace{2pt},\)\(\hspace{3pt}B(b_1\hspace{1pt},\hspace{1pt}b_2)\hspace{2pt}\)を頂点とする三角形\(OAB\hspace{2pt}\)の面積\(\hspace{1pt}S\hspace{2pt}\)は以下の公式によって求められます。

2. 三角形の面積の公式の証明(ベクトル表示)

ベクトル表示された三角形の面積の公式を導出します。

以下のような三角形\(OAB\hspace{2pt}\)において\(\hspace{1pt}\overrightarrow{OA} = \vec{a}\hspace{2pt},\hspace{2pt}\overrightarrow{OB} = \vec{b}\hspace{2pt}\)とします。
また、\(\angle AOB = \theta\hspace{2pt}\)とします。

上図の三角形の面積は、三角比による三角形の面積公式から $${S = \frac{1}{2} \hspace{1pt}|\vec{a}||\vec{b}|\sin \theta}$$ となります。

上式の両辺を二乗すると \begin{eqnarray} S^2 = && \frac{1}{4} \hspace{1pt}{|\vec{a}|}^2 {|\vec{b}|}^2 \sin^2 \theta \\[0.3em] = && \frac{1}{4} \hspace{1pt}{|\vec{a}|}^2 {|\vec{b}|}^2 (1-\cos^2 \theta) \\[0.3em] = && \frac{1}{4} (\hspace{1pt}{|\vec{a}|}^2 {|\vec{b}|}^2 - {|\vec{a}|}^2 {|\vec{b}|}^2\cos^2 \theta )\\[0.3em] \end{eqnarray}

となります。
(上記の式変形には三角比の相互関係から\(\hspace{1pt}\sin^2 \theta + \cos^2 \theta = 1\hspace{2pt}\)を用いています。)

ここで、内積の定義式から $${|\vec{a}| |\vec{b}| \cos \theta = \vec{a}\cdot \vec{b}}$$ であることから \begin{eqnarray} S^2 = && \frac{1}{4} (\hspace{1pt}{|\vec{a}|}^2 {|\vec{b}|}^2 - {|\vec{a}|}^2 {|\vec{b}|}^2\cos^2 \theta )\\[0.3em] = && \frac{1}{4} (\hspace{1pt}{|\vec{a}|}^2 {|\vec{b}|}^2 - (\hspace{1pt}\vec{a}\cdot \vec{b}\hspace{1pt})^2 )\\[0.3em] \end{eqnarray}

すなわち $${S = \frac{1}{2}\hspace{1pt}\sqrt{{|\vec{a}|}^2\hspace{1pt} {|\vec{b}|}^2 - (\hspace{1pt}\vec{a}\cdot \vec{b}\hspace{1pt})^2}}$$ と導くことができます。

3. 三角形の面積の公式の証明(成分表示)

次に、導出した三角形の面積の公式を成分表示の式にします。

三角形\(OAB\hspace{2pt}\)の頂点を\(\hspace{1pt}O(0\hspace{1pt},\hspace{1pt}0)\hspace{2pt},\)\(\hspace{3pt}A(a_1\hspace{1pt},\hspace{1pt}a_2)\hspace{2pt},\)\(\hspace{3pt}B(b_1\hspace{1pt},\hspace{1pt}b_2)\hspace{2pt}\)とします。

\(\hspace{1pt}\overrightarrow{OA} = \vec{a}\hspace{2pt},\hspace{2pt}\overrightarrow{OB} = \vec{b}\hspace{2pt}\)とすると \begin{eqnarray} {|\vec{a}|}^2 = && {a_1}^2 + {a_2}^2\\[0.3em] {|\vec{b}|}^2 = && {b_1}^2 + {b_2}^2\\[0.3em] \vec{a}\cdot \vec{b}\hspace{1pt}= && a_1 \hspace{1pt}b_1 + a_2\hspace{1pt} b_2\\[0.3em] \end{eqnarray} から

と導くことができます。
(途中の式変形で\(\hspace{1pt}\sqrt{A^2} = |A|\hspace{2pt}\)とする点に注意が必要です。)

4. 三角形の面積を求める問題

ベクトルの三角形の面積の公式を用いる問題について解説します。

問題1 | 平面における三角形の面積

問題2 | 平面における三角形の面積

問題3 | 空間における三角形の面積