直線のベクトル方程式

本項では以下の内容を解説します。

• ・直線のベクトル方程式
• ・二点を通るベクトル方程式
• ・法線によるベクトル方程式
• ・例題

1. 直線のベクトル方程式

　ベクトルを用いて直線上の点を表した式を直線のベクトル方程式といいます。
　本項では直線のベクトル方程式について解説します。　

1-1. 直線のベクトル方程式とは

　直線上の任意の点を\(P\hspace{2pt}\)とし、点\(P\hspace{2pt}\)の位置ベクトルを\(\hspace{1pt}\vec{p}\hspace{2pt}\)とします。
この直線が点\(\hspace{1pt}A\hspace{1pt}(\vec{a})\hspace{2pt}\)を通り、またベクトル\(\hspace{1pt}\vec{d}\hspace{2pt}\)に平行であるとします。

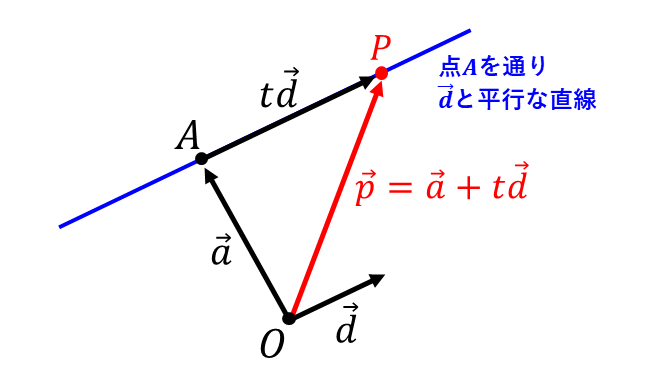
　\(\hspace{1pt}t\hspace{2pt}\)を実数としたとき、直線に平行なベクトル\(\hspace{1pt}\overrightarrow{AP}\hspace{2pt}\)は $${\overrightarrow{AP} = t \hspace{1pt}\vec{d}}$$ 　と表すことができます。

　点\(P\hspace{2pt}\)のベクトル\(\hspace{1pt}\overrightarrow{OP}\hspace{2pt}\)はベクトルの和から \begin{eqnarray} \overrightarrow{OP} = && \overrightarrow{OA} + \overrightarrow{AP} \\[0.3em] = && \vec{a} + t\hspace{1pt}\vec{d} \\[0.3em] \end{eqnarray} と表されます。

つまり、点\(\hspace{1pt}A\hspace{1pt}(\vec{a})\hspace{2pt}\)を通り、\(\vec{d}\hspace{2pt}\)に平行な直線のベクトル方程式は以下のように表されます。

上式において、\(\vec{d}\hspace{3pt}\)は直線と平行であり、直線の方向を表しています。この直線の方向を表すベクトルを方向ベクトルといいます。
　

以下の図に実数\(\hspace{1pt}t\hspace{2pt}\)を\(\hspace{3pt}t = 0\hspace{1pt},\hspace{1pt}1\hspace{1pt},\hspace{1pt}2\hspace{3pt}\)と変化させたときの点\(\hspace{1pt}P\hspace{2pt}\)の位置を示します。

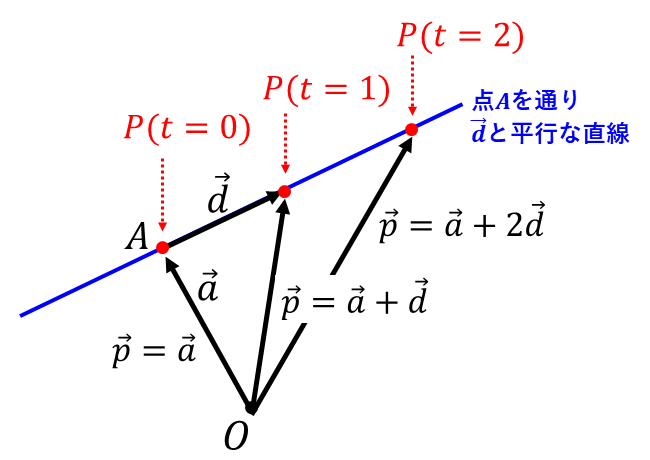
\(\hspace{1pt}t\hspace{2pt}\)を変化させたとき、\(\vec{p} = \vec{a} + t \hspace{1pt} \vec{d}\hspace{2pt}\)は

　\(\hspace{1pt}t = 0\hspace{2pt}\)のとき
　　\(\hspace{1pt}\vec{p} = \vec{a} \)

　\(\hspace{1pt}t = 1\hspace{2pt}\)のとき
　　\(\hspace{1pt}\vec{p} = \vec{a} + \vec{d}\)

　\(\hspace{1pt}t = 2\hspace{2pt}\)のとき
　　\(\hspace{1pt}\vec{p} = \vec{a} + 2 \vec{d}\)

となり、点\(A\hspace{1pt}\)を通り\(\hspace{1pt}\vec{d}\hspace{2pt}\)に平行な直線上に点\(P\hspace{2pt}\)が並ぶことが分かります。

\(\hspace{1pt}t\hspace{2pt}\)を全ての実数とすれば、点\(P\hspace{2pt}\)は点\(A\hspace{1pt}\)を通り\(\hspace{1pt}\vec{d}\hspace{2pt}\)に平行な直線上のすべての点を動きます。

1-2. 直線のベクトル方程式の成分表示

上記の直線のベクトル方程式 $${ \vec{p} = \vec{a} + t \hspace{1pt} \vec{d}}$$ を成分表示により表します。

直線上の点\(P\hspace{1pt}\)の座標を\((\hspace{1pt}x\hspace{1pt},\hspace{1pt}y\hspace{1pt})\hspace{1pt}\)とします。点\(A\hspace{1pt}(\hspace{1pt}x_1\hspace{1pt},\hspace{1pt}y_1\hspace{1pt})\hspace{1pt}\)を通り、方向ベクトル\(\hspace{2pt}\vec{d}\hspace{3pt}\)が\(\hspace{2pt}(l\hspace{1pt},\hspace{1pt}m)\hspace{2pt}\)であるとき、直線のベクトル方程式は \begin{eqnarray} (\hspace{1pt}x\hspace{1pt},\hspace{1pt}y\hspace{1pt}) = && (\hspace{1pt}x_1\hspace{1pt},\hspace{1pt}y_1\hspace{1pt}) +t\hspace{1pt}(l\hspace{1pt},\hspace{1pt}m) \\[0.3em] = && (\hspace{1pt}x_1 + l\hspace{1pt}t\hspace{1pt},\hspace{1pt}y_1 + m\hspace{1pt}t\hspace{1pt}) \\[0.3em] \end{eqnarray} となります。

　
上式の\(\hspace{1pt}t\hspace{2pt}\)を媒介変数といいます。
また、媒介変数\(\hspace{1pt}t\hspace{2pt}\)を用いて方程式を表すことを媒介変数表示といいます。

上式から媒介変数\(\hspace{1pt}t\hspace{2pt}\)を削除すれば、直線の方程式を $${m\hspace{1pt}(x-x_1) - l\hspace{1pt}(y-y_1) = 0}$$ と表せます。

1-3. 例題

2. 二点を通る直線のベクトル方程式

以下の図のように、異なる二点\(\hspace{1pt}A\hspace{1pt}(\vec{a})\hspace{2pt}\)と\(\hspace{1pt}B\hspace{1pt}(\vec{b})\hspace{2pt}\)を通る直線のベクトル方程式を導きます。

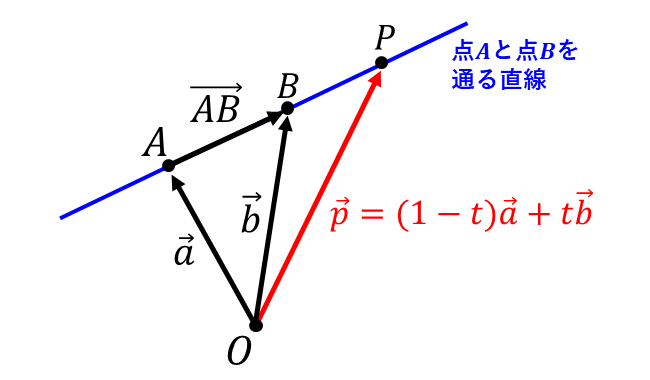
点\(A\hspace{1pt}\)を通り\(\hspace{1pt}\vec{d}\hspace{2pt}\)に平行な直線を表すベクトル方程式 $${\vec{p} = \vec{a} + t\hspace{1pt}\vec{d}}$$ より、方向ベクトル\(\hspace{1pt}\vec{d}\hspace{2pt}\)を\(\hspace{2pt}A\hspace{1pt}(\vec{a})\hspace{2pt}\)から\(\hspace{1pt}B\hspace{1pt}(\vec{b})\hspace{2pt}\)までを表すベクトル\(\hspace{1pt}\overrightarrow{AB}\hspace{2pt}\)に置き換えます。

\(\hspace{1pt}\overrightarrow{AB} = \vec{b} - \vec{a}\hspace{2pt}\)であることから、\(t\hspace{2pt}\)を実数としたとき \begin{eqnarray} \vec{p} = && \vec{a} + t\hspace{1pt}\vec{d} \\[0.3em] = && \vec{a} + t\hspace{1pt}(\vec{b} - \vec{a}) \\[0.3em] = && (1-t)\hspace{1pt}\vec{a} + t \hspace{1pt} \vec{b}\\[0.3em] \end{eqnarray} となります。

また、\(1-t = s\hspace{2pt}\)とおくと $${ \vec{p} = s \hspace{1pt}\vec{a} + t \hspace{1pt} \vec{b}\hspace{10pt}(s+t=1)}$$ と変形されます。

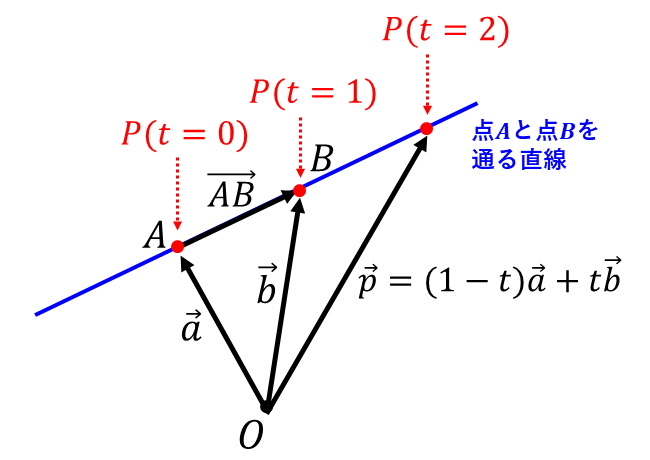
\(\hspace{1pt}t\hspace{2pt}\)を変化させたとき、\(\vec{p} =(1-t)\hspace{1pt}\vec{a} + t \hspace{1pt} \vec{b}\hspace{2pt}\)は

　\(\hspace{1pt}t = 0\hspace{2pt}\)のとき
　　\(\hspace{1pt}\vec{p} = \vec{a} \)

　\(\hspace{1pt}t = 1\hspace{2pt}\)のとき
　　\(\hspace{1pt}\vec{p} = \vec{b} \)

　\(\hspace{1pt}t = 2\hspace{2pt}\)のとき
　　\(\hspace{1pt}\vec{p} = -\vec{a} + 2 \vec{b}\)

となり、二点\(\hspace{1pt}A\hspace{1pt}(\vec{a})\hspace{2pt}\)と\(\hspace{1pt}B\hspace{1pt}(\vec{b})\hspace{2pt}\)を通る直線上に点\(P\hspace{2pt}\)が並ぶことが分かります。

2-1. 例題

3. 法線ベクトルによる直線のベクトル方程式

以下の図のように、点\(\hspace{1pt}A\hspace{1pt}(\vec{a})\hspace{2pt}\)を通り、ベクトル\(\hspace{1pt}\vec{n}\hspace{2pt}\)に垂直な直線上の任意の点\(P\hspace{2pt}\)を表す方程式を考えます。

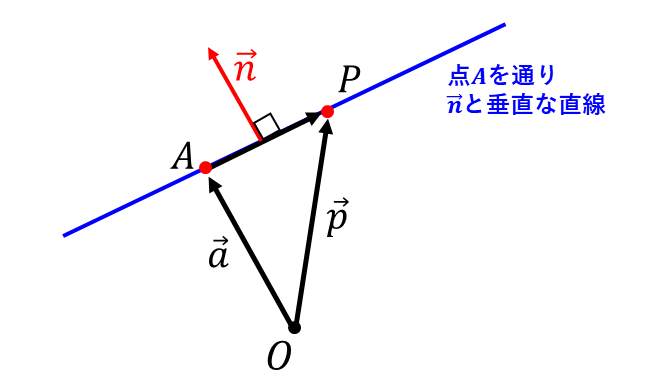
上図のように、\(\overrightarrow{AP}\hspace{1pt}\hspace{2pt}\)とベクトル\(\hspace{1pt}\vec{n}\hspace{2pt}\)が垂直であることから、内積の定義より $${\vec{n} \cdot \overrightarrow{AP} = 0}$$ となります。

また、\(\overrightarrow{AP} = \vec{p} - \vec{a}\hspace{2pt}\)であることから $${\vec{n} \cdot (\vec{p} - \vec{a}) = 0}$$ と表せます。

ある直線に対して垂直方向のベクトルを法線ベクトルといいます。上式では、\(\vec{n}\hspace{2pt}\)が直線に対する法線ベクトルです。

点\(A\hspace{1pt}\)と法線ベクトル\(\hspace{1pt}\vec{n}\hspace{2pt}\)を成分により表し、その内積を計算すると直線の方程式となります。

点\(A\hspace{1pt}(\hspace{1pt}x_1\hspace{1pt},\hspace{1pt}y_1\hspace{1pt})\)を通り、ベクトル\(\hspace{1pt}\vec{n}\hspace{2pt}\)が\(\hspace{2pt}(\hspace{1pt}m\hspace{1pt},\hspace{1pt}l\hspace{1pt})\hspace{2pt}\)であるとき、直線のベクトル方程式 $${ \vec{n} \cdot (\hspace{1pt}\vec{p}-\vec{a}\hspace{1pt}) = 0}$$ は\(\hspace{3pt}\vec{p}-\vec{a} = (x-x_1\hspace{1pt},\hspace{1pt}y-y_1)\hspace{2pt}\)であることから、内積を計算すると $${m\hspace{1pt}(x-x_1) + l\hspace{1pt}(y-y_1) = 0}$$ となります。

3-1. 例題