三角形の面積公式
本項では、三角形の面積公式 について解説します。
【1】三角形の面積公式
以下の図のような三角形\(\displaystyle {ABC}\) の面積\(\displaystyle \hspace{2pt}S \hspace{2pt}\)は以下の公式から求められます。
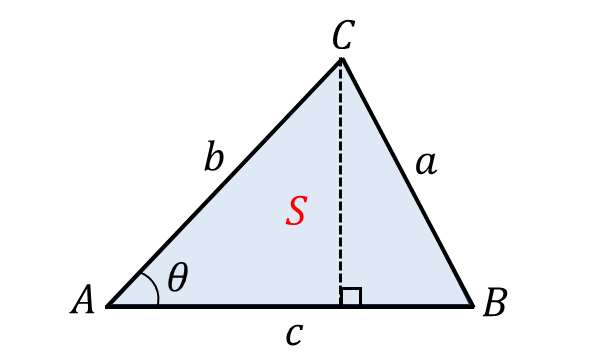
この公式から、『三角形の\(\hspace{1pt}2\hspace{2pt}\)辺の長さ』と『その\(\hspace{1pt}2\hspace{2pt}\)辺に挟まれた角の\(\hspace{1pt}\sin\hspace{2pt}\)の値』から三角形の面積を求められることが分かります。
2. 三角形の面積公式の証明
三角形の面積公式を証明します。
ここでは、\(\displaystyle S = \frac{1}{2}\hspace{1pt} b \hspace{1pt}c \hspace{1pt}\sin A\hspace{2pt}\)についてのみ証明します。他の式も同様に考えて証明することができます。
三角形\(\hspace{1pt}ABC \hspace{2pt}\)において、角\(\hspace{1pt}A\hspace{2pt}\)の大きさによって以下のように場合分けします。
(1)\(\hspace{3pt}0^\circ < A < 90^\circ\hspace{2pt}\)のとき
(2)\(\hspace{3pt} A = 90^\circ\hspace{2pt}\)のとき
(3)\(\hspace{3pt}90^\circ < A < 180^\circ\hspace{2pt}\)のとき
【(1)\(\hspace{3pt}0^\circ < A < 90^\circ\hspace{2pt}\)のとき】
以下の図のように、角\(A\hspace{2pt}\)が\(\hspace{3pt}0^\circ < A < 90^\circ\hspace{3pt}\)であるとします。
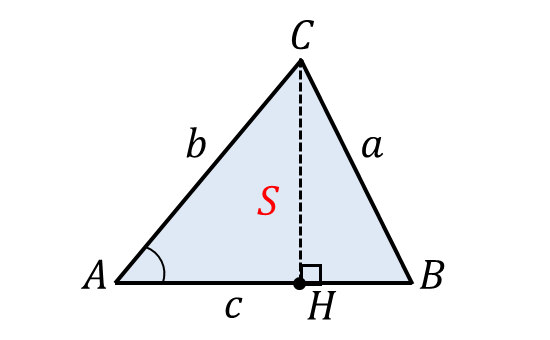
頂点\(\hspace{1pt}C\hspace{2pt}\)から辺\(\hspace{2pt}AB\hspace{2pt}\)に下した垂線の足を\(H\hspace{2pt}\)とします。
このとき、三角比の定義から $${CH = b \hspace{1pt}\sin A}$$ となります。
したがって、面積\(\hspace{1pt}S\hspace{2pt}\)は
\begin{eqnarray}
S = && \frac{1}{2}\hspace{1pt}AB\times CH\\[0.5em]
= && \frac{1}{2}\hspace{1pt} c \hspace{1pt} b \hspace{1pt} \sin A\\[0.5em]
\end{eqnarray}
となります。
【(2)\(\hspace{3pt} A = 90^\circ\hspace{2pt}\)のとき】
角\(A\hspace{2pt}\)が\(\hspace{1pt} A = 90^\circ\hspace{2pt}\)のとき、三角形は以下の図のようになります。
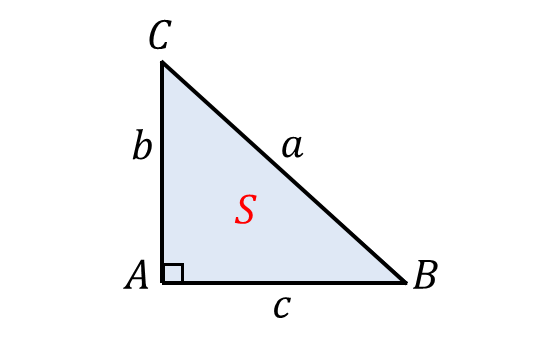
図から三角形の面積\(\hspace{1pt}S\hspace{2pt}\)は $${S = \frac{1}{2}\hspace{1pt} c \hspace{1pt} b }$$ となります。
\(\sin 90^\circ = 1\hspace{2pt}\)であるので、角\(A\hspace{2pt}\)が\(\hspace{1pt} A = 90^\circ\hspace{2pt}\)のとき\(\displaystyle \hspace{2pt}S = \frac{1}{2}\hspace{1pt} c \hspace{1pt} b \hspace{1pt} \sin A\hspace{2pt}\)が成り立ちます。
【(3)\(\hspace{3pt}90^\circ < A < 180^\circ\hspace{2pt}\)のとき】
下図のように、角\(A\hspace{2pt}\)が\(\hspace{3pt}90^\circ < A < 180^\circ\hspace{3pt}\)とします。
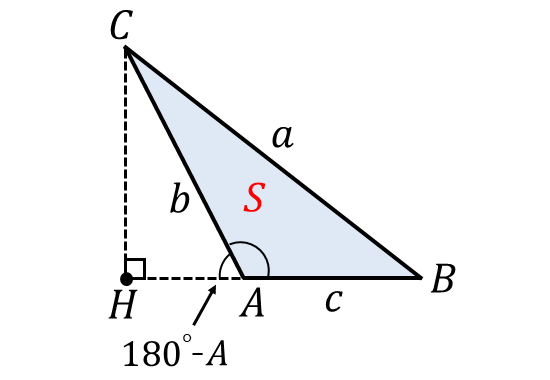
頂点\(\hspace{1pt}C\hspace{2pt}\)から辺\(\hspace{2pt}AB\hspace{2pt}\)を延長した直線に下した垂線の足を\(H\hspace{2pt}\)とします。
このとき、\(\angle \hspace{1pt} CAH = 180^\circ - A \hspace{2pt}\)となります。
ここで、180°-θの公式から
$${\sin (180^\circ - A) = \sin A}$$
であることから
\begin{eqnarray}
CH = && b \hspace{1pt}\sin (180^\circ - A)\\[0.5em]
= && b \hspace{1pt}\sin A\\[0.5em]
\end{eqnarray}
となります。
したがって、面積\(\hspace{1pt}S\hspace{2pt}\)は
\begin{eqnarray}
S = && \frac{1}{2}\hspace{1pt}AB\times CH\\[0.5em]
= && \frac{1}{2}\hspace{1pt} c \hspace{1pt} b \hspace{1pt} \sin A\\[0.5em]
\end{eqnarray}
となります。
(1)~(3)から、三角形の面積\(\hspace{1pt}S\hspace{2pt}\)は $${S = \frac{1}{2}\hspace{1pt} b \hspace{1pt}c \hspace{1pt}\sin A}$$ となります。
3. 問題と解き方
三角形の面積公式を用いる問題について解説します。
問題1 | 二辺と間の角度から面積を求める
【答え】
\(\displaystyle\hspace{1pt}S =\frac{15\sqrt{3}}{4}\)
【解答のポイント】
本問は二辺とその間の角の角度が示されているため
$${S = \frac{1}{2}\hspace{1pt} a \hspace{1pt}b \hspace{1pt}\sin C}$$
を使い面積を求めます。
【解答】
三角形の面積公式から
\begin{eqnarray}
S= && \frac{1}{2}\hspace{1pt} a \hspace{1pt}b \hspace{1pt}\sin C \\[0.3em]
= && \frac{1}{2} \cdot 3 \cdot 5 \cdot \sin 60^\circ\\[0.3em]
= && \frac{15}{2}\cdot\frac{\sqrt{3}}{2}\\[0.3em]
= && \frac{15\sqrt{3}}{4}\\[0.3em]
\end{eqnarray}
と求められます。
問題2 | 二辺と間の角度から面積を求める
【答え】
\(\displaystyle\hspace{1pt}S =5 \sqrt{2}\)
【解答のポイント】
本問は二辺とその間の角の角度が示されているため
$${S = \frac{1}{2}\hspace{1pt} a \hspace{1pt}b \hspace{1pt}\sin C}$$
を使い面積を求めます。
180°-θの公式から
$${\sin (180^\circ - A) = \sin A}$$
であることから\(\hspace{1pt}\sin 135^\circ\hspace{2pt}\)の値を求めます。
【解答】
180°-θの公式から
\begin{eqnarray}
\sin 135^\circ = && \sin (180^\circ - 45^\circ) \\[0.3em]
= && \sin 45^\circ\\[0.3em]
\end{eqnarray}
となります。
三角形の面積公式から \begin{eqnarray} S= && \frac{1}{2}\hspace{1pt} a \hspace{1pt}b \hspace{1pt}\sin C \\[0.3em] = && \frac{1}{2} \cdot 4 \cdot 5 \cdot \sin 135^\circ\\[0.3em] = && 10 \cdot \sin 45^\circ\\[0.3em] = && 10 \cdot \frac{\sqrt{2}}{2}\\[0.3em] = && 5 \sqrt{2}\\[0.3em] \end{eqnarray} と求められます。
問題3 | 三辺の長さから面積を求める
【答え】
\(\displaystyle\hspace{1pt}S =\frac{15\hspace{1pt}\sqrt{7}}{4}\)
【解答のポイント】
本問は三辺の長さのみが分かっている三角形の面積を求める問題です。
本項の面積公式を用いるためには、\(\sin\hspace{2pt}\)の値が必要であるため余弦定理
$${\cos A = \frac{b^{\hspace{1pt}2}+ c^{\hspace{1pt}2} -a^{\hspace{1pt}2}}{2\hspace{1pt}b\hspace{1pt}c}}$$
から\(\hspace{1pt}\cos A\hspace{2pt}\)の値を求め、三角比の相互関係
$${\sin^2 A + \cos^2 A = 1 }$$
から\(\hspace{1pt}\sin A\hspace{2pt}\)の値を求めます。
【解答】
余弦定理
$${\cos A = \frac{b^{\hspace{1pt}2}+ c^{\hspace{1pt}2} -a^{\hspace{1pt}2}}{2\hspace{1pt}b\hspace{1pt}c}}$$
から
\begin{eqnarray}
\cos A = && \frac{5^{\hspace{1pt}2}+ 6^{\hspace{1pt}2} -4^{\hspace{1pt}2}}{2 \cdot 5 \cdot 6} \\[0.3em]
= && \frac{3}{4}\\[0.3em]
\end{eqnarray}
となります。
三角比の相互関係 $${\sin^2 A + \cos^2 A = 1 }$$ から\(\hspace{1pt}\sin A\hspace{2pt}\)を求めます。このとき、\(\sin A > 0\hspace{2pt}\)であることから \begin{eqnarray} \sin A = && \sqrt{1-\cos^2 A} \\[0.3em] = && \sqrt{1-\left( \frac{3}{4}\right)^2} \\[0.3em] = && \frac{\sqrt{7}}{4} \\[0.3em] \end{eqnarray}
三角形の面積公式から \begin{eqnarray} S= && \frac{1}{2}\hspace{1pt} b \hspace{1pt}c \hspace{1pt}\sin A \\[0.3em] = && \frac{1}{2} \cdot 5 \cdot 6 \cdot \frac{\sqrt{7}}{4}\\[0.3em] = && \frac{15\hspace{1pt}\sqrt{7}}{4}\\[0.3em] \end{eqnarray} と求められます。