ベクトルの成分表示
本項では以下の内容を解説します。
- ・ベクトルの成分表示
- ・基本ベクトル
- ・関連する問題
【1】ベクトルの成分表示
ベクトルの成分表示について解説します。
【1-1】基本ベクトル
座標系の軸方向の単位ベクトルを基本ベクトルといいます。
基本ベクトルの記号には \(x\hspace{2pt}\)軸\(\hspace{1pt},\hspace{1pt}y\hspace{2pt}\)軸\(\hspace{1pt},\hspace{1pt}z\hspace{2pt}\)軸に対して\(\hspace{3pt}\vec{e_1}\hspace{2pt},\hspace{2pt}\vec{e_2}\hspace{2pt},\hspace{2pt}\vec{e_3}\hspace{4pt}\)という記号が使われます。
下図のように\(\hspace{2pt}x\hspace{2pt}\)軸方向と\(\hspace{2pt}y\hspace{2pt}\)軸方向の基本ベクトルをそれぞれ\(\hspace{2pt}\vec{e_1}\hspace{1pt},\hspace{1pt}\vec{e_2}\hspace{2pt}\)とします。
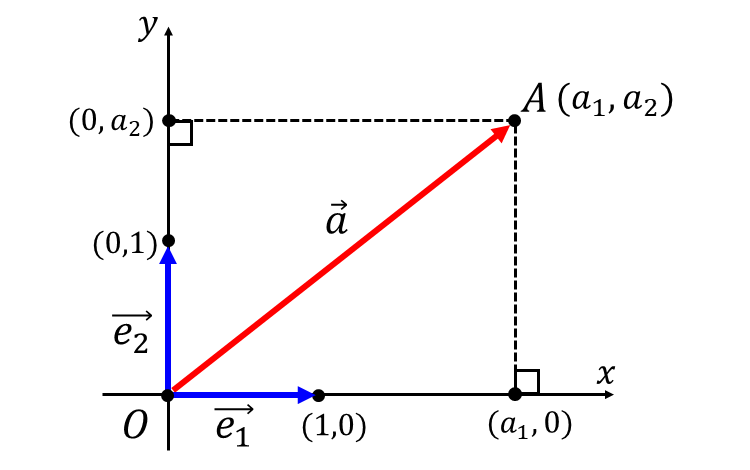
ベクトル\(\hspace{2pt}\vec{a}\hspace{2pt}\)を\(\hspace{2pt}\vec{a} = \overrightarrow{OA}\hspace{2pt}\)とし、点\(\hspace{1pt}A\hspace{2pt}\)の座標が\(\hspace{2pt}(a_1 \hspace{1pt},\hspace{1pt}a_2)\hspace{2pt}\)であるとします。
このとき、ベクトル\(\hspace{2pt}\vec{a}\hspace{2pt}\)は基本ベクトル\(\hspace{3pt}\vec{e_1}\hspace{2pt},\hspace{2pt}\vec{e_2}\hspace{3pt}\)を用いて
$${\vec{a}\hspace{2pt} = a_1 \hspace{1pt}\vec{e_1} + a_2 \hspace{1pt}\vec{e_2}}$$
と表されます。
【1-2】ベクトルの成分表示
ベクトル\(\hspace{2pt}\vec{a}\hspace{2pt}\)を基本ベクトル\(\hspace{2pt}\vec{e_1}\hspace{1pt},\hspace{1pt}\vec{e_2}\hspace{2pt}\)により $${\vec{a}\hspace{2pt} = a_1 \hspace{1pt}\vec{e_1} + a_2 \hspace{1pt}\vec{e_2}}$$ と表したとき、この\(\hspace{2pt}a_1 \hspace{1pt},\hspace{1pt}a_2\hspace{2pt}\)を\(\hspace{2pt}\vec{a}\hspace{2pt}\)の成分といいます。
以下のように基本ベクトルを省略し、成分だけでベクトルを表す表記方法をベクトルの成分表示といいます。
【1-3】成分表示されたベクトルの演算
成分表示されたベクトルの和や差は、各成分ごとに和や差を計算します。
また、成分表示されたベクトルの実数倍は、各成分を実数倍します。
【1-4】ベクトルの演算の証明
上記の成分表示されたベクトルの演算は以下のように示されます。
\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)を基本ベクトル\(\hspace{2pt}\vec{e_1}\hspace{1pt},\hspace{1pt}\vec{e_2}\hspace{2pt}\)により表すと \begin{eqnarray} \vec{a}\hspace{2pt} && = a_1 \hspace{1pt}\vec{e_1} + a_2 \hspace{1pt}\vec{e_2}\\[0.3em] \vec{b}\hspace{2pt} && = b_1 \hspace{1pt}\vec{e_1} + b_2 \hspace{1pt}\vec{e_2}\\[0.3em] \end{eqnarray} となります。この和を求めるとベクトルの演算から
となります。したがって
が成り立ちます。\(\hspace{2pt}\vec{a} - \vec{b}\hspace{2pt}\)についても同様に示されます。
また、実数倍については\(\hspace{2pt}k\hspace{2pt}\)を実数としたとき、ベクトルの演算から \begin{eqnarray} k \hspace{1pt}\vec{a}\hspace{2pt} && = k \hspace{1pt} (a_1 \hspace{1pt}\vec{e_1} + a_2 \hspace{1pt}\vec{e_2})\\[0.5em] && = k \hspace{1pt}a_1 \hspace{1pt}\vec{e_1} + k \hspace{1pt}a_2 \hspace{1pt}\vec{e_2}\\[0.5em] \hspace{2pt} && = (k \hspace{1pt}a_1 \hspace{1pt},\hspace{1pt}k \hspace{1pt} a_2)\\[0.5em] \end{eqnarray} となります。したがって $${ k\hspace{1pt}(a_1 \hspace{1pt},\hspace{1pt}a_2) = (k \hspace{1pt}a_1 \hspace{1pt},\hspace{1pt}k\hspace{1pt}a_2) }$$ が成り立ちます。
2.ベクトルの成分表示の問題
ベクトルの成分表示に関連した問題を解説します。
問題1.ベクトルの成分表示
(1) \(\vec{a} + \vec{b}\hspace{2pt}\)
(2) \(3\hspace{1pt}\vec{a} -4 \hspace{1pt}\vec{b}\hspace{2pt}\)
【答え】
\(\displaystyle (\hspace{1pt}0\hspace{1pt},\hspace{1pt}5)\hspace{2pt}\)
【解説】
成分表示されたベクトルの和は、各成分の和から求めます。
\begin{eqnarray}
\vec{a} + \vec{b} && = (\hspace{1pt}1\hspace{1pt},\hspace{1pt}3) + (\hspace{1pt}-1\hspace{1pt},\hspace{1pt}2)\\[0.5em]
&& = (\hspace{1pt}1-1\hspace{1pt},\hspace{1pt}3+2)\\[0.5em]
&& = (\hspace{1pt}0\hspace{1pt},\hspace{1pt}5)\\[0.5em]
\end{eqnarray}
【答え】
\(\displaystyle (\hspace{1pt}7\hspace{1pt},\hspace{1pt}1)\hspace{2pt}\)
【解説】
成分表示されたベクトルの実数倍は、各成分を実数倍します。
\begin{eqnarray}
3\hspace{1pt}\vec{a} -4 \hspace{1pt}\vec{b} && = 3 \hspace{1pt}(\hspace{1pt}1\hspace{1pt},\hspace{1pt}3) -4 \hspace{1pt}(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}2)\\[0.5em]
&& = \hspace{1pt}(\hspace{1pt}3\hspace{1pt},\hspace{1pt}9) + \hspace{1pt}(\hspace{1pt}4\hspace{1pt},\hspace{1pt}-8)\\[0.5em]
&& = (\hspace{1pt}3+4\hspace{1pt},\hspace{1pt}9-8)\\[0.5em]
&& = (\hspace{1pt}7\hspace{1pt},\hspace{1pt}1)\\[0.5em]
\end{eqnarray}
問題2.大きさを求める問題
【答え】
\(\displaystyle |\vec{a}| =\hspace{2pt}\sqrt{13}\hspace{2pt}\)
【解説】
成分表示されたベクトル\(\hspace{2pt}\vec{a} =(\hspace{1pt}a_1\hspace{1pt},\hspace{1pt}a_2) \hspace{2pt}\)の大きさ\(\hspace{2pt}|\vec{a}|\hspace{2pt}\)は以下のように求められます。
$${|\vec{a}| = \sqrt{{a_1}^2 + {a_2}^2} }$$
よって、問題のベクトルの大きさは
$${|\vec{a}| = \sqrt{2^2 + 3^2} = \sqrt{13}}$$
と求められます。