ベクトルの演算
本項では以下の内容を解説します。
- ・ベクトルの演算(加法・減法・実数倍)
- ・ベクトルの演算に関連する問題
【1】ベクトルの演算
2つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の和は、\(\vec{b}\hspace{2pt}\)の始点を\(\hspace{1pt}\vec{a}\hspace{1pt}\)の終点に平行移動したときの『\(\hspace{1pt}\vec{a}\hspace{1pt}\)の始点から\(\hspace{1pt}\vec{b}\hspace{1pt}\)の終点までのベクトル』となります。
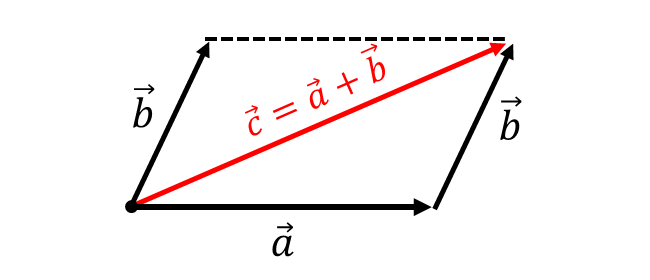
\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の和を\(\hspace{2pt}\vec{c}\hspace{2pt}\)とすると $${ \vec{c} = \vec{a} +\vec{b}}$$ と表されます。
ベクトルの加法について以下の交換法則・結合法則が成り立ちます。
【2】逆ベクトルと零ベクトル
逆ベクトルと零ベクトルについて解説します。
【2-1】逆ベクトル
ベクトル\(\hspace{2pt}\vec{a}\hspace{3pt}\)と同じ大きさで向きが反対のベクトルを逆ベクトルといいます。
逆ベクトルは\(\hspace{2pt}\vec{a}\hspace{3pt}\)に負の記号を付けた\(\hspace{1pt}-\vec{a}\hspace{2pt}\)と表されます。
また、始点\(\hspace{1pt}A\hspace{1pt}\)、終点\(\hspace{1pt}B\hspace{2pt}\)のベクトルを\(\hspace{1pt}\overrightarrow{AB}\hspace{2pt}\)とすると、その逆ベクトルは始点と終点が反対となるので\(\hspace{1pt}\overrightarrow{BA}\hspace{1pt}\)となります。
【2-2】零ベクトル
大きさが\(\hspace{2pt}0\hspace{2pt}\)のベクトルを零ベクトルといい、\(\vec{0}\hspace{2pt}\)と表します。
零ベクトルは、大きさが\(\hspace{2pt}0\hspace{2pt}\)であるので、始点と終点が一致したベクトルとなります。
零ベクトル\(\hspace{2pt}\vec{0}\hspace{2pt}\)は逆ベクトルと以下の関係があります。
【3】ベクトルの減法
2つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の差は、『\(\hspace{2pt}\vec{a}\hspace{3pt}\)』と『\(\hspace{2pt}\vec{b}\hspace{2pt}\)の逆ベクトル\(\hspace{1pt}-\vec{b}\hspace{1pt}\)』の和から求めます。
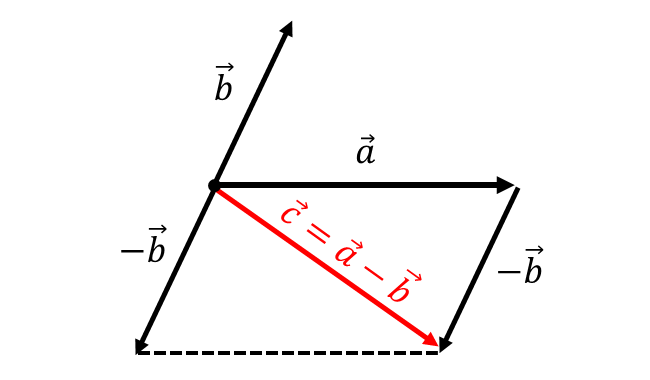
\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の差を\(\hspace{2pt}\vec{c}\hspace{2pt}\)とすると $${\vec{c} = \vec{a} -\vec{b}}$$ と表されます。
【4】ベクトルの実数倍
ベクトル\(\hspace{1pt}\vec{a}\hspace{1pt}\hspace{2pt}\)と実数\(\hspace{1pt}k\hspace{2pt}\)に対し、ベクトル\(\hspace{1pt}\vec{a}\hspace{1pt}\hspace{2pt}\)の\(\hspace{1pt}k\hspace{2pt}\)倍を\(\hspace{1pt}k \hspace{1pt}\vec{a}\hspace{2pt}\)と表します。
\(\hspace{1pt}k > 0\hspace{2pt}\)であるとき、\(\hspace{1pt}k \hspace{1pt}\vec{a}\hspace{2pt}\)は\(\hspace{1pt}\vec{a}\hspace{2pt}\)と同じ向きで大きさが\(\hspace{1pt}|\vec{a}|\hspace{2pt}\)の\(\hspace{1pt}k\hspace{2pt}\)倍のベクトルを表します。
また、\(\hspace{1pt}k < 0\hspace{2pt}\)であるとき、\(\hspace{1pt}k \hspace{1pt}\vec{a}\hspace{3pt}\)は\(\hspace{2pt}\vec{a}\hspace{3pt}\)と反対向きで大きさが\(\hspace{1pt}|\vec{a}|\hspace{2pt}\)の\(\hspace{1pt}|k|\hspace{2pt}\)倍のベクトルを表します。
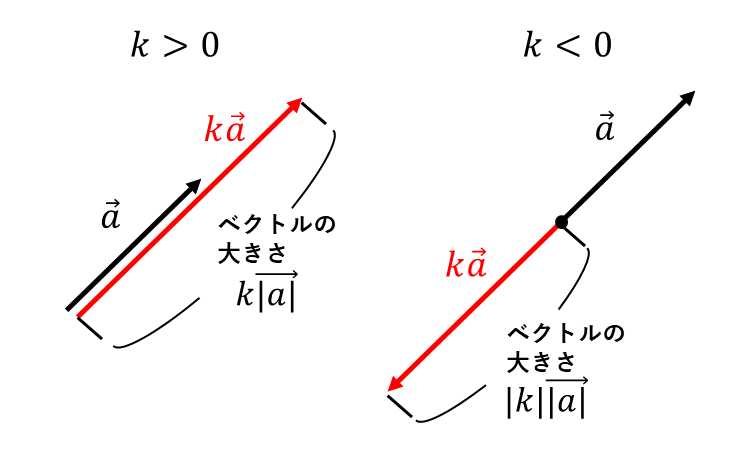
\(\hspace{2pt}k\hspace{1pt},\hspace{1pt}l\hspace{2pt}\)を実数とするとき、ベクトル\(\hspace{1pt}\vec{a}\hspace{2pt}\)の実数倍について以下が成り立ちます。
5.ベクトルの演算の問題
ベクトルの演算に関連する問題を解説します。
問題1
(1) \(\hspace{1pt}\vec{a} +\vec{b}\hspace{1pt}\)
(2) \(\hspace{1pt}\vec{a} -\vec{b}\hspace{1pt}\)
(3) \(\hspace{1pt}\vec{a} +3 \hspace{1pt}\vec{b} - \vec{c}\hspace{1pt}\)

【問題(1)の答え】

【問題(1)の解説】
2つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の和\(\hspace{2pt}\vec{a}\hspace{1pt}+\vec{b}\hspace{1pt}\hspace{2pt}\)は、\(\vec{b}\hspace{2pt}\)の始点を\(\hspace{1pt}\vec{a}\hspace{1pt}\)の終点に平行移動させ、『\(\hspace{2pt}\vec{a}\hspace{2pt}\)の始点から\(\hspace{2pt}\vec{b}\hspace{3pt}\)の終点までのベクトル』を図示します。
【問題(2)の答え】

【問題(2)の解説】
2つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の差\(\hspace{2pt}\vec{a}\hspace{1pt}-\vec{b}\hspace{1pt}\hspace{2pt}\)は、『\(\hspace{2pt}\vec{a}\hspace{2pt}\)』と『\(\hspace{1pt}\vec{b}\hspace{2pt}\)の逆ベクトル\(\hspace{1pt}-\vec{b}\hspace{1pt}\)』の和と考えます。
そこで、\(\vec{b}\hspace{2pt}\)と同じ大きさで反対方向のベクトル\(\hspace{2pt}-\vec{b}\hspace{2pt}\)の始点を\(\hspace{1pt}\vec{a}\hspace{1pt}\)の終点に平行移動させ、『\(\hspace{1pt}\vec{a}\hspace{1pt}\)の始点から\(\hspace{2pt}-\vec{b}\hspace{2pt}\)の終点までのベクトル』を図示します。
【問題(3)の答え】

【問題(3)の解説】
3つのベクトルの和\(\hspace{2pt}\vec{a}+3\hspace{1pt}\vec{b}-\hspace{1pt}\vec{c}\hspace{3pt}\)を図示します。
\(3\hspace{1pt}\vec{b}\hspace{3pt}\)は\(\hspace{2pt}\vec{b}\hspace{3pt}\)と同じ方向で\(\hspace{2pt}3\hspace{1pt}\)倍の大きさのベクトルです。また、\(\hspace{1pt}-\vec{c}\hspace{3pt}\)は\(\hspace{2pt}\vec{c}\hspace{3pt}\)と同じ大きさで反対方向のベクトルです。
\(\hspace{1pt}3\hspace{1pt}\)つのベクトルを平行移動し、『\(\hspace{1pt}\vec{a}\hspace{1pt}\)の始点から\(\hspace{1pt}-\hspace{1pt}\vec{c}\hspace{3pt}\)の終点までのベクトル』を図示します。
問題2
$${3\hspace{1pt}(\vec{a} +\vec{b}) +2\hspace{1pt}(\vec{a} - \vec{b})}$$
【答え】
\(\hspace{1pt}5\hspace{1pt}\vec{a} +\vec{b}\hspace{1pt}\)
【解説】
ベクトルの加法・減法・実数倍の計算は、通常の文字式と同じように計算をすることができます。
\begin{eqnarray}
&&3\hspace{1pt}(\vec{a} +\vec{b}) +2\hspace{1pt}(\vec{a} - \vec{b})\\[0.5em]
&& = 3\hspace{1pt}\vec{a} + 3\hspace{1pt}\vec{b} +2\hspace{1pt}\vec{a} - 2\hspace{1pt}\vec{b}\\[0.5em]
&& = 5\hspace{1pt}\vec{a} + \vec{b} \\[0.5em]
\end{eqnarray}
問題3
$${3\hspace{1pt}\vec{x} - 2\hspace{1pt}\vec{a} = 2\hspace{1pt}(\vec{x} -\vec{b})}$$
【答え】
\(\hspace{1pt}\vec{x} = 2(\hspace{1pt}\vec{a} -\hspace{1pt}\vec{b})\hspace{1pt}\)
【解説】
問題2と同様に、通常の文字式と同じように計算をします。
\begin{eqnarray}
3\hspace{1pt}\vec{x} - 2\hspace{1pt}\vec{a} &=& 2\hspace{1pt}(\vec{x} -\vec{b})\\[0.5em]
3\hspace{1pt}\vec{x} - 2\hspace{1pt}\vec{a} &=& 2\hspace{1pt}\vec{x} -2\hspace{1pt}\vec{b}\\[0.5em]
\hspace{1pt}3\vec{x} - 2\hspace{1pt}\vec{x} &=& 2\hspace{1pt}\vec{a} -2\hspace{1pt}\vec{b}\\[0.5em]
\hspace{1pt}\vec{x} &=& 2(\hspace{1pt}\vec{a} -\hspace{1pt}\vec{b})\\[0.5em]
\end{eqnarray}