単位ベクトル
本項では以下の内容を解説します。
- ・単位ベクトル
- ・単位ベクトルに関連する問題
【1】単位ベクトルとは
単位ベクトルとは、大きさが\(\hspace{2pt}1\hspace{2pt}\)のベクトルのことをいいます。
単位ベクトルの記号には\(\hspace{2pt}\vec{e}\hspace{2pt}\)という記号がよく使われます。
・単位ベクトルの求め方
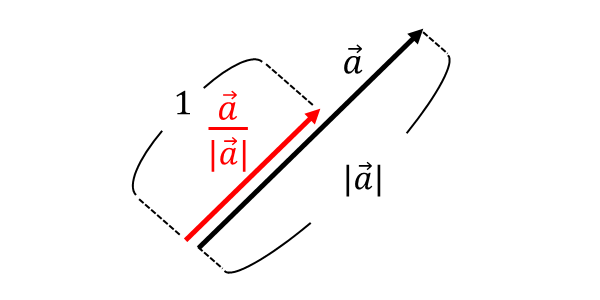
ベクトル\(\hspace{2pt}\vec{a}\hspace{2pt}\)と同じ向きの単位ベクトル\(\hspace{2pt}\vec{e}\hspace{2pt}\)は以下の式から求めることができます。
上式は、下図のように\(\hspace{2pt}\vec{a}\hspace{2pt}\)をそのベクトルの大きさ\(\hspace{2pt}|\vec{a}|\hspace{2pt}\)で割ることで、向きは\(\hspace{2pt}\vec{a}\hspace{2pt}\)のままで大きさが\(\hspace{2pt}1\hspace{2pt}\)の単位ベクトルに変換されることを意味しています。
2. 単位ベクトルの問題
単位ベクトルに関連する問題を解説します。
問題1. 同じ向きの単位ベクトル
【答え】
\(\displaystyle\hspace{2pt}\left( \frac{3}{5} , \frac{4}{5}\right)\hspace{2pt}\)
【解説】
まず、\(\vec{a} = (\hspace{1pt}3\hspace{1pt},\hspace{1pt}4\hspace{1pt}) \hspace{2pt}\)の大きさ\(\hspace{2pt}|\vec{a}| \hspace{2pt}\)を求めます。
$${|\vec{a}| = \sqrt{3^2 + 4^2} = 5}$$
よって、\(\hspace{2pt}\vec{a} = (\hspace{1pt}3\hspace{1pt},\hspace{1pt}4\hspace{1pt}) \hspace{2pt}\)と同じ向きの単位ベクトルは
\begin{eqnarray}
\frac{\vec{a}}{|\vec{a}|} = && \frac{1}{5}(\hspace{1pt}3\hspace{1pt},\hspace{1pt}4\hspace{1pt})\\[0.5em]
= && \left( \frac{3}{5} , \frac{4}{5}\right) \\[0.5em]
\end{eqnarray}
と求められます。
問題2. 平行な単位ベクトル
【答え】
\(\displaystyle\hspace{2pt}\left( \frac{3}{5} , \frac{4}{5}\right) \hspace{1pt},\hspace{1pt}\left( -\frac{3}{5} , -\frac{4}{5}\right)\hspace{2pt}\)
【解説】
問題1とは異なり、平行な単位ベクトルを求める点に注意が必要です。
平行な単位ベクトルは\(\hspace{2pt}\vec{a} \hspace{2pt}\)の反対方向の単位ベクトルも含むため、
$${\pm \frac{\vec{a}}{|\vec{a}|}}$$
から求めます。
まず、\(\vec{a} = (\hspace{1pt}3\hspace{1pt},\hspace{1pt}4\hspace{1pt}) \hspace{2pt}\)の大きさ\(\hspace{2pt}|\vec{a}| \hspace{2pt}\)は $${|\vec{a}| = \sqrt{3^2 + 4^2} = 5}$$ であることから\(\hspace{2pt}\vec{a} = (\hspace{1pt}3\hspace{1pt},\hspace{1pt}4\hspace{1pt}) \hspace{2pt}\)と平行な単位ベクトルは \begin{eqnarray} \pm \frac{\vec{a}}{|\vec{a}|} = && \pm \frac{1}{5}(3,4)\\[0.5em] = && \pm \left( \frac{3}{5} , \frac{4}{5}\right) \\[0.5em] \end{eqnarray} すなわち $${\left( \frac{3}{5} , \frac{4}{5}\right) \hspace{1pt},\hspace{1pt}\left( -\frac{3}{5} , -\frac{4}{5}\right)}$$ となります。