ベクトルの内積

本項では以下の内容を解説します。

• ・内積とは
• ・内積の定義
• ・ベクトルのなす角
• ・内積の性質
• ・平行条件、垂直条件

1. 内積とは

ベクトルの内積について解説します。

1-1. 内積の定義

\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)のなす角度を\(\hspace{2pt}\theta\hspace{3pt}\)\(\hspace{2pt}(0^\circ \leqq \theta \leqq 180^\circ)\hspace{2pt}\)とします。
このとき、以下の式で定義される値を\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の内積といい、\(\vec{a} \cdot \vec{b}\hspace{2pt}\)と表記します。

1-2. 内積の意味

内積の計算を一言で説明すると
　"\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)に対し、『\(\hspace{1pt}\vec{a}\hspace{2pt}\)の大きさ』と『\(\hspace{1pt}\vec{b}\hspace{3pt}\)の\(\hspace{2pt}\vec{a}\hspace{3pt}\)方向の成分の大きさ』をかけ合わせた値" となります。

(内積\(\hspace{2pt}|\vec{a}| \hspace{1pt}|\vec{b}| \cos \theta \hspace{2pt}\)は\(\hspace{2pt}a\hspace{1pt},\hspace{1pt}b\hspace{2pt}\)を入れ替えても値が変わらないため、『\(\hspace{1pt}\vec{b}\hspace{2pt}\)の大きさ』と『\(\hspace{1pt}\vec{a}\hspace{3pt}\)の\(\hspace{2pt}\vec{b}\hspace{3pt}\)方向の成分の大きさ』をかけ合わせた値と同じとなります。)

・角度θが鋭角のとき

　まず、なす角度が鋭角である場合の内積の計算について考えます。

　\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)のなす角度が\(\hspace{2pt}\theta\hspace{3pt}\)\(\hspace{2pt}(0^\circ \leqq \theta \leqq 90^\circ)\hspace{2pt}\)であるとき、\(2\hspace{2pt}\)つのベクトルの始点をそろえて描いた図を以下に示します。

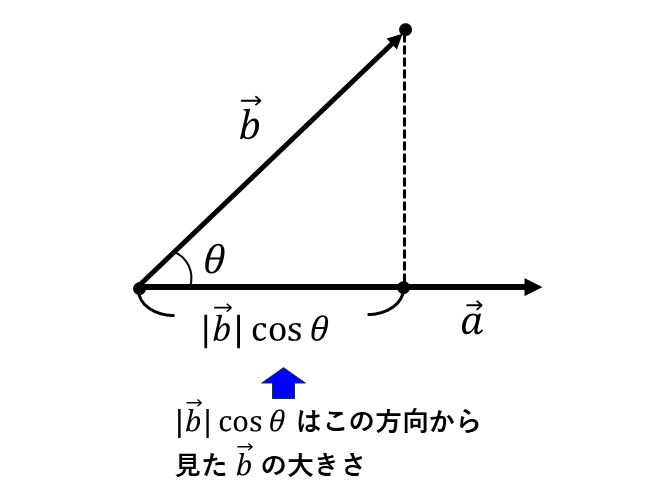
　このとき、\(|\vec{b}| \cos \theta\hspace{2pt}\)は\(\hspace{2pt}\vec{b}\hspace{2pt}\)を\(\hspace{2pt}\vec{a}\hspace{2pt}\)に対して垂直な方向から見たときの大きさとなります。つまり、\(|\vec{b}| \cos \theta\hspace{2pt}\)は\(\hspace{2pt}\vec{b}\hspace{3pt}\)の\(\hspace{2pt}\vec{a}\hspace{3pt}\)方向の成分の大きさを表しています。

　すなわち、内積\(\hspace{2pt}\vec{a} \cdot \vec{b} = |\vec{a}| \hspace{1pt}|\vec{b}| \cos \theta\hspace{2pt}\)は『\(\hspace{1pt}\vec{a}\hspace{2pt}\)の大きさ』と『\(\hspace{1pt}\vec{b}\hspace{3pt}\)の\(\hspace{2pt}\vec{a}\hspace{3pt}\)方向の成分の大きさ』をかけ合わせた値を表しています。
　

　上図から、\(|\vec{b}| \cos \theta\hspace{2pt}\)は\(\hspace{2pt}\vec{a}\hspace{2pt}\)と同じ向きであるときに最も大きくなります。
また、\(|\vec{b}| \cos \theta\hspace{2pt}\)は\(\hspace{2pt}\theta\hspace{2pt}\)が\(\hspace{2pt}90^\circ\hspace{2pt}\)に近づくほど小さくなり、\(\theta = 90^\circ\hspace{2pt}\)では\(\hspace{2pt}|\vec{b}| \cos \theta = 0\hspace{2pt}\)となります。

　つまり、\(2\hspace{2pt}\)つのベクトルの方向が一致するとき内積\(\hspace{2pt}\vec{a}\cdot\vec{b}\hspace{2pt}\)は最大となります。
　また、\(\theta\hspace{2pt}\)が\(\hspace{2pt}90^\circ\hspace{2pt}\)に近づくほど内積\(\hspace{2pt}\vec{a}\cdot\vec{b}\hspace{2pt}\)の値は小さくなり、\(2\hspace{2pt}\)つのベクトルが垂直のとき\(\hspace{2pt}\vec{a}\cdot\vec{b}=0\hspace{2pt}\)となります。

・角度θが鈍角のとき

\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)のなす角度が\(\hspace{2pt}\theta\hspace{3pt}\)\(\hspace{2pt}(90^\circ < \theta \leqq 180^\circ)\hspace{2pt}\)であるとき、\(2\hspace{2pt}\)つのベクトルの始点をそろえて描いた図を以下に示します。

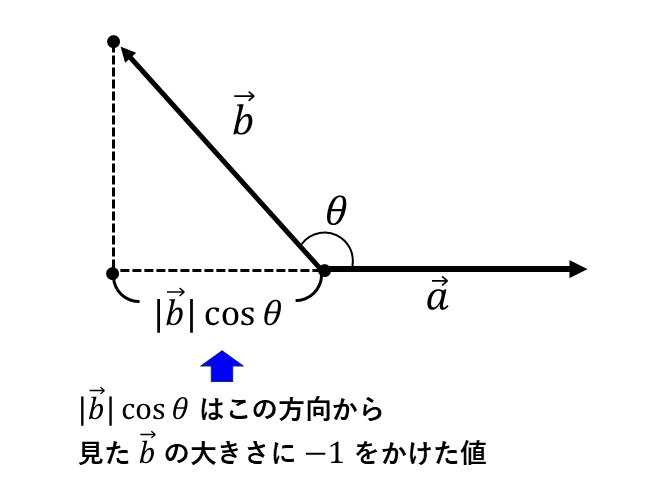
　このとき、\(|\vec{b}| \cos \theta\hspace{2pt}\)は\(\hspace{2pt}\cos \theta < 0\hspace{2pt}\)であることから、\(\vec{b}\hspace{2pt}\)を\(\hspace{2pt}\vec{a}\hspace{2pt}\)に対して垂直な方向から見たときの大きさに負の記号を付けた値となります。

　つまり、内積は\(\hspace{2pt}2\hspace{2pt}\)つのベクトルのなす角が鈍角である場合に負の値となります。
\(\hspace{2pt}2\hspace{2pt}\)つのベクトルが反対方向の成分を持っていれば内積が負となることから、『内積はベクトルの向きの違いを符号で表す』と考えると分かりやすくなります。

例題

2.成分表示の内積

また、\(\vec{a} = (a_1\hspace{1pt},\hspace{1pt}a_2)\hspace{1pt},\hspace{1pt}\vec{b} = (b_1\hspace{1pt},\hspace{1pt}b_2)\hspace{2pt}\)であるとき、内積は以下の式から求められます。

　
空間のベクトル\(\hspace{2pt}\vec{a} = (a_1\hspace{1pt},\hspace{1pt}a_2\hspace{1pt},\hspace{1pt}a_3)\hspace{1pt},\hspace{1pt}\vec{b} = (b_1\hspace{1pt},\hspace{1pt}b_2\hspace{1pt},\hspace{1pt}b_3)\hspace{2pt}\)場合は以下の式から求められます。

2-1.成分表示の内積の証明

成分表示による内積 $${\vec{a} \cdot \vec{b} = a_1 \hspace{1pt} b_1 + a_2 \hspace{1pt} b_2}$$ は以下のように証明されます。

以下の図のように、\(\vec{a} = \overrightarrow{OA}\hspace{1pt},\hspace{1pt}\vec{b} = \overrightarrow{OB}\hspace{1pt},\hspace{1pt}\angle AOB = \theta \hspace{3pt}\)とします。

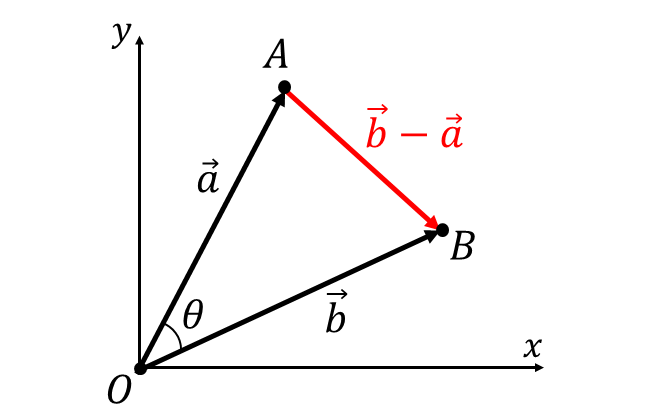
三角形\(OAB\hspace{2pt}\)に余弦定理を用いると、以下が成り立ちます。

ここで\(\hspace{2pt}AB = |\vec{b} - \vec{a}|\hspace{2pt},\hspace{1pt}OA = |\vec{a}|\hspace{2pt},\hspace{1pt}OB = |\vec{b}|\hspace{2pt},\)\(\hspace{2pt}OA \cdot OB \cdot \cos \theta = \vec{a} \cdot \vec{b}\hspace{2pt}\)であることから(1)式は以下のように表されます。

よって

すなわち $${\vec{a} \cdot \vec{b} = a_1 \hspace{1pt}b_1 + a_2 \hspace{1pt}b_2}$$ が成り立ちます。

成分表示の内積の例題

3.ベクトルのなす角

\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)の内積の定義 $${\vec{a} \cdot \vec{b} = |\vec{a}| \hspace{1pt}|\vec{b}| \cos \theta}$$ から\(\hspace{2pt}2\hspace{2pt}\)つのベクトルのなす角\(\hspace{2pt}\theta\hspace{2pt}\)\(\hspace{2pt}( \hspace{1pt}0^\circ \leqq \theta \leqq 180^\circ \hspace{1pt})\hspace{2pt}\)を以下のように求めることができます。

ベクトルのなす角の例題

4.内積の性質

内積の演算で成り立つ式について解説します。

4-1.内積の演算

ベクトルの内積には以下の式が成り立ちます。\(\hspace{2pt}k\hspace{2pt}\)を実数です。

上記の式は、\(\vec{a} = (a_1\hspace{1pt},\hspace{1pt}a_2)\hspace{1pt},\hspace{1pt}\vec{b} = (b_1\hspace{1pt},\hspace{1pt}b_2)\hspace{2pt},\)\(\hspace{1pt}\vec{c} = (c_1\hspace{1pt},\hspace{1pt}c_2)\hspace{2pt}\)と成分で表示して計算することで証明できます。

例として上記の(2)式 $${(\vec{a} +\vec{b}\hspace{1pt}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}}$$ を証明します。

\(\hspace{2pt}\vec{a} +\vec{b} = (a_1 +b_1 \hspace{1pt},\hspace{1pt}a_2 + b_2 )\hspace{2pt}\)であることから左辺を変形すると

したがって $${(\vec{a} +\vec{b}\hspace{1pt}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}}$$ が成り立ちます。

4-2.同じベクトル同士の内積

同じベクトル同士の内積について以下の式が成り立ちます。

上記の式は、内積の定義式から導くことができます。

(4)式の左辺を内積の定義式から計算すると \begin{eqnarray} \hspace{10pt} \vec{a} \cdot \vec{a} && = | \vec{a} |\hspace{1pt} |\vec{a} | \cos 0^\circ \\[0.5em] && = {|\vec{a}|}^{\hspace{1pt}2} \\[0.5em] \end{eqnarray} となります。

また、(5)式は\(\hspace{2pt}|\vec{a}| \geqq 0\hspace{2pt}\)であるので(4)式から $${|\vec{a}| = \sqrt{\vec{a} \cdot \vec{a}}}$$ となります。

例題

5.内積による平行・垂直条件

\(\vec{a} = (a_1\hspace{1pt},\hspace{1pt}a_2)\hspace{1pt},\hspace{1pt}\vec{b} = (b_1\hspace{1pt},\hspace{1pt}b_2)\hspace{2pt}\)\(\hspace{2pt}(\vec{a} \neq \vec{0} \hspace{1pt},\hspace{1pt}\vec{b} \neq \vec{0} )\hspace{2pt}\)であるとき、\(2\hspace{2pt}\)つのベクトルが平行・垂直である条件は以下の式で表されます。

5-1.平行条件の導出

平行条件は内積の定義

から導かれます。

\(\hspace{2pt}2\hspace{2pt}\)つのベクトルが平行であるとき、なす角\(\hspace{2pt}\theta\hspace{2pt}\)は\(\hspace{2pt}0^\circ\hspace{2pt}\)(同じ向き)もしくは\(\hspace{2pt}180^\circ\hspace{2pt}\)(反対方向)のどちらかとなります。

このとき、\(\cos \theta = \pm 1\hspace{2pt}\)となるため、内積の定義式から $${ \pm |\vec{a}| \hspace{1pt}|\vec{b}| = a_1 \hspace{1pt} b_1 + a_2 \hspace{1pt} b_2\cdots (1)}$$ となります。

\(|\vec{a}| \hspace{1pt}|\vec{b}|\hspace{2pt}\)をベクトルの成分で表すと $${|\vec{a}| \hspace{1pt}|\vec{b}| = \sqrt{{a_1}^{\hspace{1pt}2} + {a_2}^{\hspace{1pt}2}}\hspace{1pt} \sqrt{{b_1}^{\hspace{1pt}2} + {b_2}^{\hspace{1pt}2}}}$$ となります。

(1)の両辺を二乗すると

したがって\(\hspace{2pt}2\hspace{2pt}\)つのベクトルが平行のとき $${a_1 \hspace{1pt}b_2 - a_2 \hspace{1pt}b_1 = 0}$$ となります。
　

内積の定義式から平行条件を導くとやや計算が難しいですが、直線の傾きに着目して同じ式を簡単に導くこともできます。

点\(A\hspace{1pt}(a_1\hspace{1pt},\hspace{1pt}a_2)\hspace{1pt},\hspace{2pt}\)点\(\hspace{1pt}B \hspace{1pt}(b_1\hspace{1pt},\hspace{1pt}b_2)\hspace{2pt},\hspace{2pt}\)原点\(\hspace{1pt}O\hspace{1pt}(0\hspace{1pt},\hspace{1pt}0)\hspace{2pt}\)とするとき、直線\(\hspace{1pt}OA\hspace{1pt}\)と直線\(\hspace{1pt}OB\hspace{1pt}\)が平行であるとき、直線の傾きが等しければよいので $${\frac{a_2}{a_1} = \frac{b_2}{b_1}}$$ となります。

上式を整理すると $${a_1 \hspace{1pt}b_2 - a_2 \hspace{1pt}b_1 = 0}$$ が導かれます。

内積の平行条件をそのまま覚えると記号を間違いやすいので、こちらの方法で導出してしまうのも手です。

5-2.垂直条件の導出

垂直条件も内積の定義

から導かれます。

\(\hspace{2pt}2\hspace{2pt}\)つのベクトルが垂直であるとき、なす角\(\hspace{2pt}\theta\hspace{2pt}\)は\(\hspace{2pt}90^\circ\hspace{2pt}\)であるので\(\hspace{2pt}\cos \theta = 0\hspace{2pt}\)となります。

よって、内積の定義式から $${a_1 \hspace{1pt} b_1 + a_2 \hspace{1pt} b_2 = 0}$$ が導かれます。

平行条件の例題

垂直条件の例題