ベクトルとは

本項では以下の内容を解説します。

• ・ベクトルとは
• ・ベクトルの相当
• ・例題

【1】ベクトルとは

\(\hspace{1pt}1 \hspace{1pt}, \hspace{1pt}-2\hspace{1pt}, \hspace{1pt}\pi\hspace{2pt}\)といった数字はスカラーといい、大きさのみを表す量です。

一方、向き と 大きさ を表す量をベクトルといいます。
ベクトルは下図のように向きのある矢印で表します。

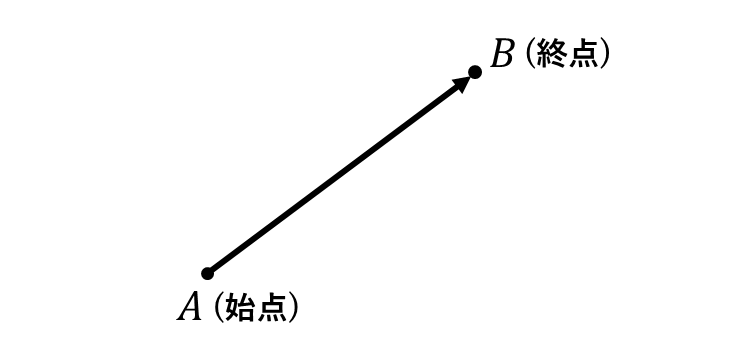
上図において\(A\hspace{1pt}\)を始点、\(B\hspace{2pt}\)を終点といいます。このようなベクトルを始点・終点の文字と矢印を用いて\(\hspace{2pt}\overrightarrow{AB}\hspace{2pt}\)と書きます。
また、ベクトルは\(\hspace{1pt}1\hspace{2pt}\)つの文字に矢印を付けて\(\hspace{2pt}\overrightarrow{a}\hspace{2pt},\hspace{2pt}\overrightarrow{b}\hspace{1pt}\hspace{2pt}\)などと表すこともあります。

線分\(\hspace{1pt}AB\hspace{2pt}\)の長さをベクトルの大きさといいます。ベクトルの大きさは\(\hspace{2pt}|\overrightarrow{AB}|\hspace{2pt}\)と表します。

【2】ベクトルの相当

ベクトルは向きと大きさを表す量であり、その位置は問題にしません。
つまり、\(2\hspace{1pt}\)つのベクトルの向きと大きさが等しければ、等しいベクトルとなります。

そのため以下の図のように、\(\hspace{1pt}\overrightarrow{AB}\hspace{2pt}\)を平行移動した\(\hspace{2pt}\overrightarrow{CD}\hspace{2pt}\)は、向きと大きさが等しいことから等しいベクトルとなります。

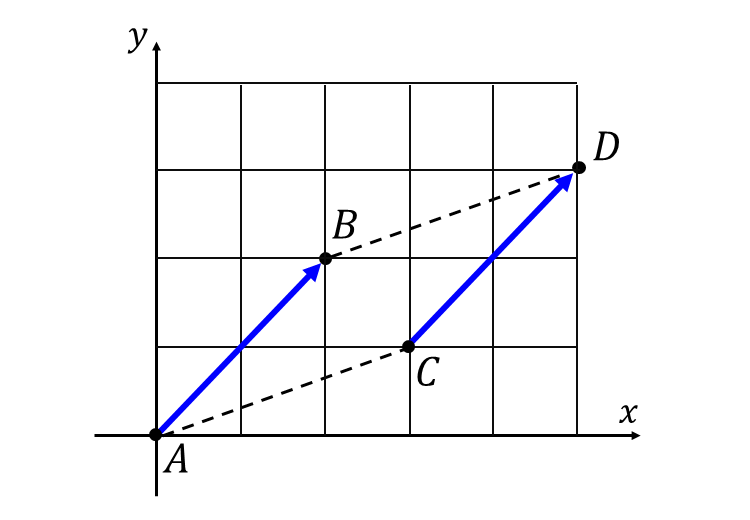
\(\hspace{1pt}2\hspace{1pt}\)つのベクトル\(\hspace{2pt}\overrightarrow{AB}\hspace{1pt},\hspace{1pt}\overrightarrow{CD}\hspace{2pt}\)が等しいことを以下のように表します。

例題

ベクトルの相当に関連する例題を解説します。

　

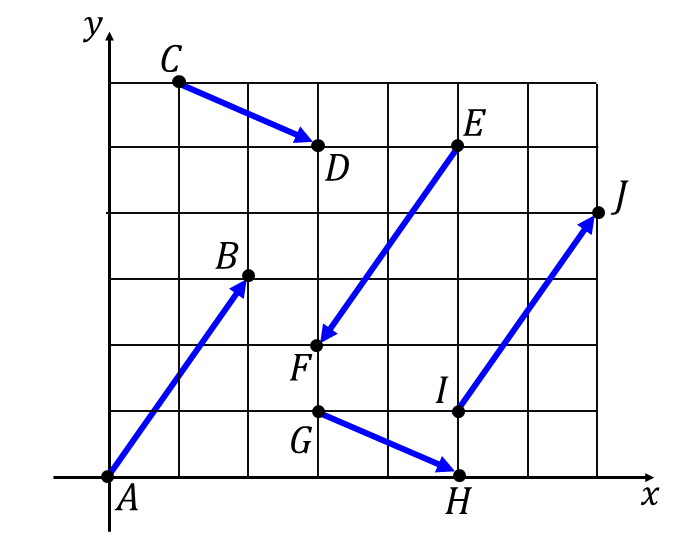
【答え】
　\(\displaystyle \hspace{1pt}\overrightarrow{AB} \hspace{2pt}\)と\(\hspace{1pt}\overrightarrow{IJ}\hspace{2pt}, \)\(\hspace{2pt}\overrightarrow{CD} \hspace{2pt}\)と\(\hspace{1pt}\overrightarrow{GH}\)
　

　【解説】
問題文の『等しいベクトルの組』とは大きさと向きの等しい2つのベクトルのことです。
\(\hspace{1pt}\overrightarrow{AB} \hspace{2pt}\)と\(\hspace{1pt}\overrightarrow{IJ}\hspace{2pt}, \)\(\hspace{2pt}\overrightarrow{CD} \hspace{2pt}\)と\(\hspace{1pt}\overrightarrow{GH}\hspace{2pt}\)は大きさと向きが等しいため、等しいベクトルの組となります。

一方、\(\hspace{1pt}\overrightarrow{EF}\hspace{1pt}\)は\(\hspace{1pt}\overrightarrow{AB} , \overrightarrow{IJ}\hspace{1pt}\)と大きさが等しいですが、向きが反対方向のベクトルです。

このような大きさが等しく、反対方向のベクトルを逆ベクトルといいます。

---