ベクトルの英語表現
本項では以下の内容を解説しています。
- ・ベクトルの記号と読み方
- ・内積と外積の英語表現
- ・関連用語の一覧
【1】ベクトルの英語表現
数学のベクトルは、英語でvectorといいます。
また、日本語でベクトル量を意味するvector quantityと表記することもあります。
【1-1】ベクトルの記号と英語の読み方
ベクトルとは、向き(direction)と大きさ(magnitude)を持った量です。
ベクトルに対比する量としてスカラー量(scalar quantity)があります。スカラー量とは、大きさのみを持つ量のことをいいます。
ベクトルは以下の図のように、始点(initial point)と終点(terminal point)により定義されます。
また、ベクトルを矢印(arrow)に見立てて、始点をtail,終点をheadという場合もあります。

点Aから点Bまでのベクトルを表す\(\hspace{1pt}\large{\overrightarrow{AB}}\hspace{2pt}\)を英語で読むときは、"vector A B"といいます。
また、ベクトルをある記号で表した\(\hspace{1pt}\large{\vec{u}}\hspace{2pt}\)などを英語で読むときは、"vector u"といいます
【1-2】ベクトルの成分
ベクトルは座標の成分によって表記されます。
下図のような\(\hspace{1pt}\large{xy}\hspace{2pt}\)平面では、ベクトル\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)の成分は\(\hspace{1pt}\large{(a_x, a_y)}\hspace{2pt}\)などと表記します。
ここで、\(\hspace{1pt}\large{(a_x,a_y)}\hspace{2pt}\)は、"a sub x (comma) a sub y"と読みます。
subは下付き文字を表すsubscriptを略した言い方です。

ベクトルを成分で表した『\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\) = (2,3)』を英語で説明すると、"Vector a is equal to 2 (comma) 3."などといいます。
もしくは、別の表現方法として、『\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)のx成分は2、y成分は3』と説明することもできます。英語では、"the x component of vector a is 2, the y component of vector a is 3."などといいます。
"component"はベクトルの成分を意味する用語です。
・単位ベクトルの英語表現
また、別の表記方法として、各軸方向の単位ベクトルによって表記することもあります。
単位ベクトルとは、大きさが1であるベクトルのことをいい、英語では"unit vector"といいます。
単位ベクトルによく使われる記号として、\(\hspace{1pt}\large{\hat{i}}\hspace{2pt}\)は\(\hspace{1pt}\large{x}\hspace{2pt}\)軸方向 、\(\hspace{1pt}\large{\hat{j}}\hspace{2pt}\)は\(\hspace{1pt}\large{y}\hspace{2pt}\)軸方向の単位ベクトルとして使われます。\(\hspace{1pt}\large{\hat{i}}\hspace{2pt}\)は英語で"i hat"と読みます。
以下の表に、\(\hspace{1pt}\large{x}\hspace{2pt}\)軸、\(\hspace{1pt}\large{y}\hspace{2pt}\)軸、\(\hspace{1pt}\large{z}\hspace{2pt}\)軸でよく使用される単位ベクトルを示します。
| 記号 | 成分 | 読み方 |
|---|---|---|
| \(\hspace{1pt}\large{\hat{i}}\hspace{2pt}\) | \(\hspace{1pt}\large{(1,0,0)}\hspace{2pt}\) | i hat |
| \(\hspace{1pt}\large{\hat{j}}\hspace{2pt}\) | \(\hspace{1pt}\large{(0,1,0)}\hspace{2pt}\) | j hat |
| \(\hspace{1pt}\large{\hat{k}}\hspace{2pt}\) | \(\hspace{1pt}\large{(0,0,1)}\hspace{2pt}\) | k hat |
例えば、単位ベクトルを使用して『\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\) = (2,3)』を表現すると、『\(\hspace{1pt}\large{\vec{a}} = 2 \boldsymbol{\hat{i}}+ 3 \boldsymbol{\hat{j}}\hspace{2pt}\)』となります。
『\(\hspace{1pt}\large{\vec{a}} = 2 \boldsymbol{\hat{i}}+ 3 \boldsymbol{\hat{j}}\hspace{2pt}\)』を英語で説明すると、"Vector a is equal to 2 times i hat plus 3 times j hat."などといいます。
【1-3】ベクトルの大きさ
ベクトルの大きさは、英語で"magnitude"もしくは"length"といいます。
ベクトルが\(\hspace{1pt}\large{\vec{a}=(a_x,a_y,a_z)}\hspace{2pt}\)であるとき、その大きさ\(\hspace{1pt}\large{|\vec{a}|}\hspace{2pt}\)は以下のようになります。
ここで、『ベクトル\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)の大きさは\(\hspace{1pt}\large{\sqrt{{a_x}^2 + {a_y}^2 + {a_z}^2}}\hspace{2pt}\)です。』を英語で表現すると、
"The magnitude of vector a is the square root of a sub x squared plus a sub y squared plus a sub z squared."などといいます。
the square root of Xは『Xの2乗根』、X squaredは『Xの2乗』を表す用語です。詳しくはべき乗の記事に記載しています。
【2】ベクトルの内積と外積の英語表現
本章では、ベクトルの分野でよく使用される内積と外積の英語表現について解説します。
【2-1】ベクトルの内積
ベクトルの内積を英語で"dot product"といいます。
\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の内積は、\(\hspace{1pt}\large{\vec{a} \cdot \vec{b}}\hspace{2pt}\)と表記します。
英語では、"dot product of vectors a and b"などといいます。
\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の内積は、以下の式により計算されます。
ここで、\(\hspace{1pt}\large{\theta}\hspace{2pt}\)は以下の図のように、2つのベクトルのなす角度を表します。
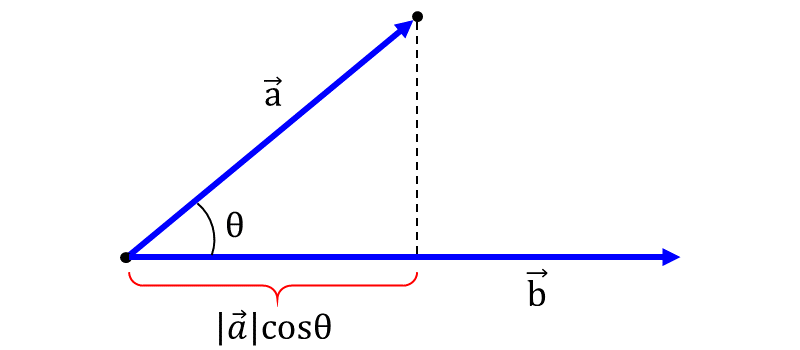
『\(\hspace{1pt}\large{\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos \theta}\hspace{2pt}\)』を英語で表現すると、"The dot product of vectors a and b is equal to magnitude of vector a times magnitude of vector b times cosine theta (of the angle between two vectors)."などといいます。
【2-2】ベクトルの外積
ベクトルの外積を英語で"cross product"といいます。
\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の外積は、\(\hspace{1pt}\large{\vec{a} \times \vec{b}}\hspace{2pt}\)と表記します。
英語では、"cross product of vectors a and b"といいます。
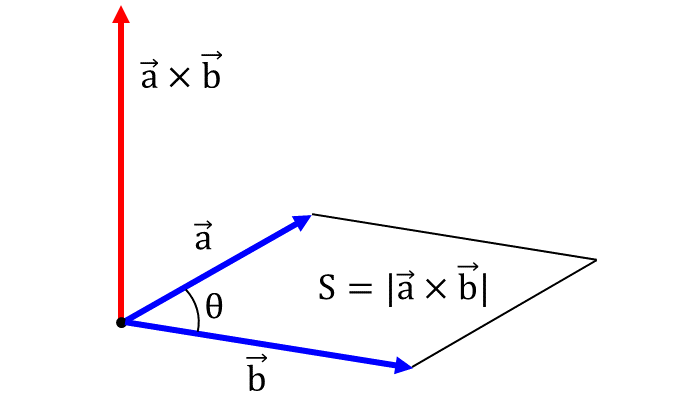
\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の外積は、以下のような式で定義されます。
\(\hspace{1pt}\large{\theta}\hspace{2pt}\)は上図のような2つのベクトルのなす角度、\(\hspace{1pt}\large{\vec{n}}\hspace{2pt}\)は2つのベクトルに垂直な方向の単位ベクトルを表します。
『\(\hspace{1pt}\large{\vec{a} \times \vec{b} = |\vec{a}| |\vec{b}| \sin \theta \ \vec{n}}\hspace{2pt}\)』を英語で表現すると、
"The cross product of vectors a and b / is equal to / magnitude of vector a / times magnitude of vector b / times sine theta (of the angle between two vectors) / times unit vector n (at right angles to both a and b)."などといいます。
また、外積の大きさは、\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)によって作られる平行四辺形の面積の大きさとなります。
外積の大きさと2つのベクトルで作られる平行四辺形の関係を英語で説明すると、以下のようになります。
"The magnitude of the cross product of vectors a and b is equal to the area of a parallelogram formed by the vectors."となります。
また、外積により計算されるベクトルの向きは、\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の両方に垂直な方向となります。
英語でこの関係を説明すると、
"The direction of the cross product of vectors a and b is perpendicular to a and b."などといいます。
\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)の成分が\(\hspace{1pt}\large{(a_x,a_y,a_z)}\hspace{2pt}\)、\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の成分が\(\hspace{1pt}\large{(b_x,b_y,b_z)}\hspace{2pt}\)であるとき、\(\hspace{1pt}\large{\vec{a}}\hspace{2pt}\)と\(\hspace{1pt}\large{\vec{b}}\hspace{2pt}\)の外積は、以下の行列式によって計算されます。 $$\large{ \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ a_x & a_y& a_z\\ b_x & b_y& b_z \end{vmatrix} }$$
上記のような3行3列の行列の行列式は、英語で"The determinant of 3 by 3 matrix."といいます。
行列の英語表現については、行列の英語表現の記事に記載しています。
【3】ベクトルに関連する英語の用語
ベクトルに関連する英語の用語を以下の表にまとめています。
| 用語 | 意味 |
|---|---|
| vector | ・ベクトル |
| vector quantity | ・ベクトル量 |
| direction | ・(ベクトルの)向き |
| magnitude, length |
・(ベクトルの)大きさ |
| initial point | ・始点 |
| terminal point | ・終点 |
| segment | ・線分 |
| unit vector | ・単位ベクトル |
| component | ・(ベクトルの)成分 |
| dot product | ・内積 |
| cross product | ・外積 |
| parallelogram | ・平行四辺形 |
| is perpendicular to | ・~に垂直 |
また、以下にベクトルに関連した英語用語の一覧を示します。
| 用語 | 意味 |
|---|---|
| position Vector | ・位置ベクトル |
| normal Vector | ・法線ベクトル |
| basis Vector | ・基底ベクトル |
| vector Addition | ・ベクトルの加算 |
| vector Subtraction | ・ベクトルの減算 |
| vector Field | ・ベクトル場 |
| gradient | ・勾配 |
| divergence | ・発散 |