ベクトルの内分点・外分点の公式
本項では以下の内容を解説します。
- ・ベクトルの内分点
- ・ベクトルの外分点
- ・例題
【1】ベクトルの内分点の公式
点\(\hspace{1pt}A\hspace{2pt}\)と点\(\hspace{1pt}B\hspace{2pt}\)を結ぶ線分\(\hspace{2pt}AB\hspace{2pt}\)上に点\(\hspace{2pt}P\hspace{2pt}\)が存在し $${AP : PB = m : n}$$ となる点\(\hspace{1pt}P\hspace{2pt}\)のことを内分点といいます。
\(\vec{a} = \overrightarrow{OA}\hspace{2pt},\hspace{1pt}\vec{b} = \overrightarrow{OB}\hspace{2pt}\)とするとき、線分\(\hspace{1pt}AB\hspace{2pt}\)を\(\hspace{2pt}m : n\hspace{2pt}\)に内分する点\(\hspace{1pt}P\hspace{2pt}\)の位置ベクトル\(\hspace{2pt}\vec{p} = \overrightarrow{OP}\hspace{2pt}\)は以下のように表されます。
ベクトルの内分点の公式の導出
以下の図のような点\(\hspace{1pt}A\hspace{2pt}\)\((\vec{a})\hspace{2pt}\)と点\(\hspace{1pt}B\hspace{2pt}\)\((\vec{b})\hspace{2pt}\)を結ぶ線分\(AB\hspace{2pt}\)を\(\hspace{2pt}m : n\hspace{2pt}\)に内分する点\(\hspace{1pt}P\hspace{2pt}\)の位置ベクトル\(\hspace{1pt}\vec{p}\hspace{2pt}\)を求めます。
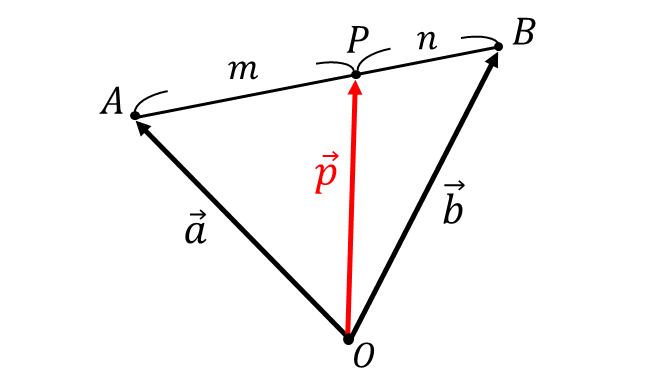
上図から $${\overrightarrow{AP} = \frac{m}{m+n} \overrightarrow{AB}}$$ となります。
ここで、\(\overrightarrow{AP} = \vec{p} - \vec{a}\hspace{2pt},\hspace{1pt}\overrightarrow{AB} = \vec{b} - \vec{a}\hspace{2pt}\)であるので $${(\vec{p} - \vec{a}) = \frac{m}{m+n} (\vec{b} - \vec{a})}$$ すなわち \begin{eqnarray} \vec{p} = && \vec{a} + \frac{m}{m+n} (\vec{b} - \vec{a})\\[0.3em] = && \frac{n \hspace{1pt}\vec{a} + m \hspace{1pt}\vec{b}}{m+n}\\[0.3em] \end{eqnarray} となります。
【2】ベクトルの外分点の公式
点\(\hspace{1pt}A\hspace{2pt}\)と点\(\hspace{1pt}B\hspace{2pt}\)を結ぶ線分\(\hspace{2pt}AB\hspace{2pt}\)の延長線上に点\(\hspace{2pt}Q\hspace{2pt}\)が存在し $${AQ : QB = m : n}$$ となる点\(\hspace{1pt}P\hspace{2pt}\)のことを外分点といいます。
\(\vec{a} = \overrightarrow{OA}\hspace{2pt},\hspace{1pt}\vec{b} = \overrightarrow{OB}\hspace{2pt}\)とするとき、線分\(\hspace{1pt}AB\hspace{2pt}\)を\(\hspace{2pt}m : n\hspace{2pt}\)に外分する点\(\hspace{1pt}Q\hspace{2pt}\)の位置ベクトル\(\hspace{2pt}\vec{q} = \overrightarrow{OQ}\hspace{2pt}\)は以下のように表されます。
ベクトルの外分点の公式の導出
以下の図のような点\(\hspace{1pt}A\hspace{2pt}\)\((\vec{a})\hspace{2pt}\)と点\(\hspace{1pt}B\hspace{2pt}\)\((\vec{b})\hspace{2pt}\)を結ぶ線分\(AB\hspace{2pt}\)を\(\hspace{2pt}m : n\hspace{2pt}\)に外分する点\(\hspace{1pt}Q\hspace{2pt}\)の位置ベクトル\(\hspace{1pt}\vec{q}\hspace{2pt}\)を求めます。
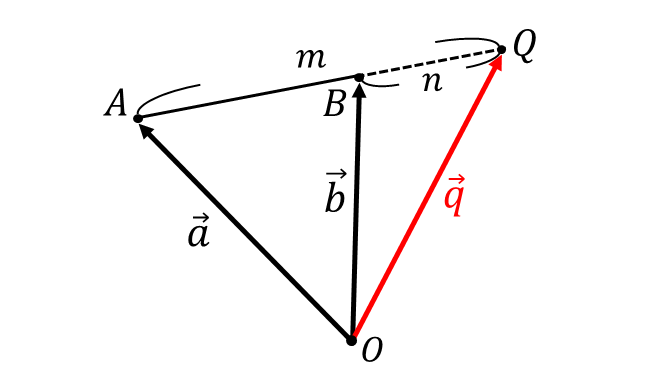
上図から $${\overrightarrow{AQ} = \frac{m}{m-n} \overrightarrow{AB}}$$ となります。
ここで、\(\overrightarrow{AQ} = \vec{q} - \vec{a}\hspace{2pt},\hspace{1pt}\overrightarrow{AB} = \vec{b} - \vec{a}\hspace{2pt}\)であるので $${(\vec{q} - \vec{a}) = \frac{m}{m-n} (\vec{b} - \vec{a})}$$ すなわち \begin{eqnarray} \vec{q} = && \vec{a} + \frac{m}{m-n} (\vec{b} - \vec{a})\\[0.3em] = && \frac{- n \hspace{1pt} \vec{a}+ m \hspace{1pt}\vec{b}}{m -n}\\[0.3em] \end{eqnarray} となります。
3.内分点・外分点の例題
ベクトルの内分点・外分点の例題を解説します。
内分点の位置ベクトル
【答え】
\(\displaystyle \vec{p} =\frac{3 \hspace{1pt} \vec{a}+ 2 \hspace{1pt}\vec{b}}{5}\)
【解答のポイント】
内分点の位置ベクトルを求める公式
$${\vec{p} = \frac{n \hspace{1pt} \vec{a}+ m \hspace{1pt}\vec{b}}{m+n}}$$
から計算します。
【解答】
内分点の位置ベクトルは
\begin{eqnarray}
\vec{p} = && \frac{n \hspace{1pt} \vec{a}+ m \hspace{1pt}\vec{b}}{m+n}\\[0.3em]
= && \frac{3 \hspace{1pt} \vec{a}+ 2 \hspace{1pt}\vec{b}}{2+3}\\[0.3em]
= && \frac{3 \hspace{1pt} \vec{a}+ 2 \hspace{1pt}\vec{b}}{5}\\[0.3em]
\end{eqnarray}
と求められます。
外分点の位置ベクトル
【答え】
\(\displaystyle \vec{q} =-3 \hspace{1pt} \vec{a}+ 4\hspace{1pt}\vec{b}\)
【解答のポイント】
外分点の位置ベクトルを求める公式
$${\vec{q} = \frac{- n \hspace{1pt} \vec{a}+ m \hspace{1pt}\vec{b}}{m -n}}$$
から計算します。
【解答】
外分点の位置ベクトルは
\begin{eqnarray}
\vec{q} = && \frac{-n \hspace{1pt} \vec{a}+ m \hspace{1pt}\vec{b}}{m-n}\\[0.3em]
= && \frac{-3 \hspace{1pt} \vec{a}+ 4\hspace{1pt}\vec{b}}{4-3}\\[0.3em]
= && -3 \hspace{1pt} \vec{a}+ 4\hspace{1pt}\vec{b}\\[0.3em]
\end{eqnarray}
と求められます。