円のベクトル方程式

本項では以下の内容を解説します。

• ・円のベクトル方程式
• ・公式の導出
• ・例題

1. 円のベクトル方程式

　ベクトルを用いて円周上の点を表す式を"円のベクトル方程式"といいます。

　円のベクトル方程式は、以下の二つの条件により導かれます。

　　[1] 中心と円周上の点の距離が一定
　　[2] 直径に対する円周角が直角

　本項では[1],[2]のそれぞれの条件で導きます。　

[1] 中心と円周上の点の距離が一定

　中心が点\(\hspace{1pt}C\hspace{1pt}(\vec{c\hspace{1pt}})\)、半径\(\hspace{1pt}r\hspace{2pt}\)である円周上の任意の点を\(P\hspace{1pt}(\vec{p}\hspace{2pt})\)とします。

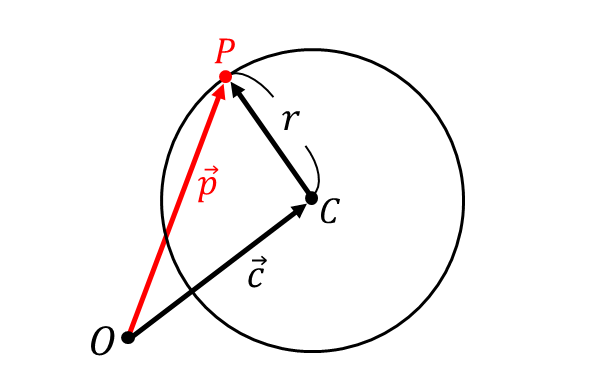
この円を表すベクトル方程式は、\(|\overrightarrow{CP}| = r\hspace{2pt}\)と一定であることから $${|\hspace{1pt}\vec{p} - \vec{c}\hspace{1pt}| =r }$$ と表すことができます。

　
上式の両辺を二乗すると $${|\hspace{1pt}\vec{p} - \vec{c}\hspace{1pt}|^{\hspace{1pt}2} =r^{\hspace{1pt}2} }$$ となり、上式は内積の定義より $${(\hspace{1pt}\vec{p} - \vec{c}\hspace{1pt})\cdot (\hspace{1pt}\vec{p} - \vec{c}\hspace{1pt})=r^{\hspace{1pt}2} }$$ となります。
(内積の定義から\(\hspace{2pt}\vec{a}\cdot\vec{a} = |a|^{\hspace{1pt}2}\hspace{2pt}\)であることを用いています。)

ここで\(\hspace{3pt}\vec{p} = (x\hspace{1pt},\hspace{1pt}y)\hspace{2pt},\vec{c} = (x_1\hspace{1pt},\hspace{1pt}y_1)\hspace{2pt}\)と成分で表し、内積を計算すると $${(x-x_1)^2 + (y-y_1)^2 = r^2}$$ となり、円の方程式が導かれます。

[2] 直径に対する円周角が直角

　円周角の定理から、円の直径を\(AB\hspace{2pt}\)としたとき、円周上の点\(P\hspace{2pt}\)に対して\(\hspace{1pt}\angle APB = 90^\circ\hspace{3pt}\)が成り立ちます。

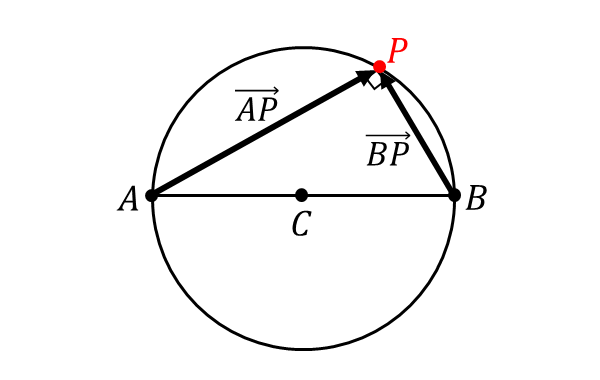
　この関係をベクトルの内積によって表すと\(\hspace{1pt}\overrightarrow{AP}\cdot\overrightarrow{BP}=0\hspace{2pt}\)となります。
\(\hspace{1pt}\overrightarrow{AP} = \vec{p} - \vec{a}\hspace{2pt},\hspace{2pt}\overrightarrow{BP} = \vec{p} - \vec{b}\hspace{3pt}\)であることから、円のベクトル方程式は $${( \vec{p} - \vec{a}) \cdot (\vec{p} - \vec{b}) = 0}$$ と表されます。

2. 円のベクトル方程式の例題

　円のベクトル方程式に関連した例題について解説します。

例題1. 中心と半径からベクトル方程式を求める

例題2. 2点の座標から円の方程式を求める