ベクトルの分解
本項では以下の内容を解説します。
- ・ベクトルの分解とは
- ・和の式と差の式
- ・関連する問題
【1】ベクトルの分解
ベクトルの分解について解説します。
【1-1】ベクトルの分解とは
ベクトルの分解とは、ある任意のベクトルを平行でない\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)で表すことをいいます。
ベクトルの分解を図で表すと以下のようになります。
下図のように任意のベクトル\(\hspace{2pt}\vec{p}=\overrightarrow{OP} \hspace{2pt}\)を平行でない\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a} = \overrightarrow{OA} \hspace{1pt},\hspace{1pt}\vec{b} = \overrightarrow{OB}\hspace{2pt}\)で表します。
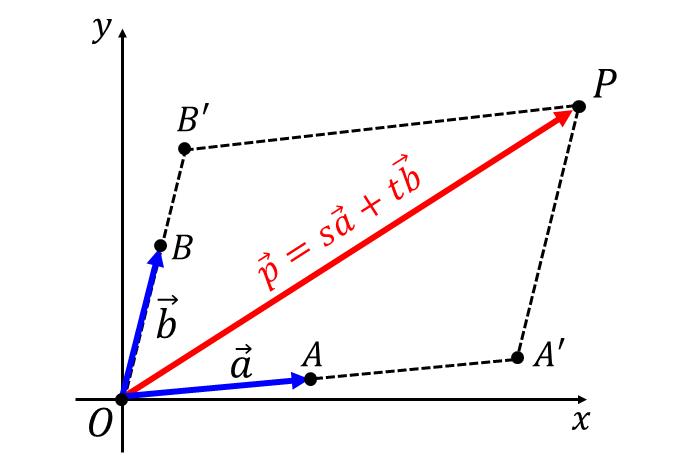
\(\hspace{2pt}OA \hspace{2pt}\)を延長した直線と点\(\hspace{1pt}P\hspace{2pt}\)を通り\(\hspace{2pt}OB \hspace{3pt}\)と平行な直線の交点を\(\hspace{2pt}A'\)、\(OB \hspace{2pt}\)を延長した直線と点\(\hspace{1pt}P\hspace{2pt}\)を通り\(\hspace{2pt}OA \hspace{3pt}\)と平行な直線の交点を\(\hspace{2pt}B\hspace{1pt}'\hspace{2pt}\)とします。
このように点\(\hspace{1pt}A\hspace{1pt}'\hspace{1pt},\hspace{1pt}B\hspace{1pt}'\hspace{2pt}\)を定めると、\(\overrightarrow{OA\hspace{1pt}'}\hspace{2pt}\)は\(\overrightarrow{OA}\hspace{2pt}\)と平行であり、また\(\hspace{2pt}\overrightarrow{OB\hspace{1pt}'}\hspace{2pt}\)は\(\overrightarrow{OB}\hspace{2pt}\)と平行となります。
よって、\(\overrightarrow{OA\hspace{1pt}'} = s \hspace{1pt}\overrightarrow{OA}\hspace{3pt}\)と\(\hspace{2pt}\overrightarrow{OB\hspace{1pt}'} = t \hspace{1pt}\overrightarrow{OB}\hspace{2pt}\)を満たす実数の組\(\hspace{2pt}(s\hspace{1pt},\hspace{1pt}t)\hspace{2pt}\)をただ\(\hspace{2pt}1\hspace{2pt}\)つ定めることができます。
このとき、ベクトルの和から\(\hspace{2pt}\overrightarrow{OP} \hspace{2pt}\)は以下のように表されます。 \begin{eqnarray} \overrightarrow{OP} = && \overrightarrow{OA\hspace{1pt}'} + \overrightarrow{OB\hspace{1pt}'}\\[0.3em] = && s \hspace{1pt}\overrightarrow{OA} + t \hspace{1pt}\overrightarrow{OB}\\[0.3em] \end{eqnarray} すなわち $${\vec{p} = s \hspace{1pt} \vec{a}+ t \hspace{1pt}\vec{b}}$$ と表されます。
【2】ベクトルの分解の公式
あるベクトルを\(\hspace{2pt}2\hspace{2pt}\)つのベクトルに分解する問題では、以下の公式をよく使います。
【2-1】和の式
和の形で分解する公式
$${\overrightarrow{AB} = \overrightarrow{A\square} + \overrightarrow{\square B}}$$
はベクトルの和の性質を利用した公式です。
この公式は、ある点を経由してベクトルを分解する場合に有効です。
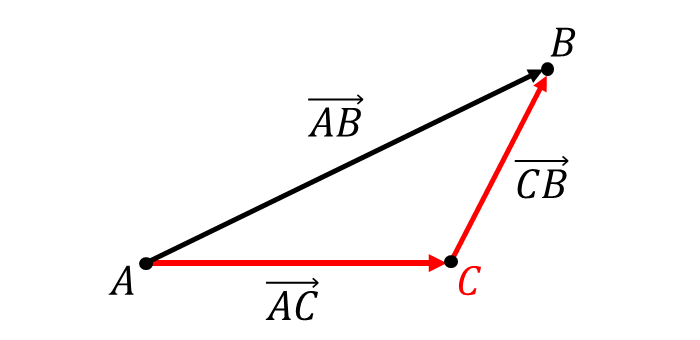
例えば、\(\overrightarrow{AB}\hspace{2pt}\)を ある点\(\hspace{2pt}C\hspace{2pt}\)を経由して分解すると、以下の図のように\(\hspace{1pt}\overrightarrow{AB}\hspace{2pt}\)は\(\hspace{2pt}\overrightarrow{AC}\hspace{2pt}\)と\(\hspace{2pt}\overrightarrow{CB}\hspace{2pt}\)ベクトルの和となることから
$${\overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{C B}}$$
となります。
【2-2】差の式
差の形で分解する公式 $${\overrightarrow{AB} = \overrightarrow{\square B} - \overrightarrow{\square A}}$$ は、ある点を基準として\(\hspace{2pt}\overrightarrow{AB}\hspace{2pt}\)を\(\hspace{2pt}2\hspace{2pt}\)つのベクトルに分解する公式です。
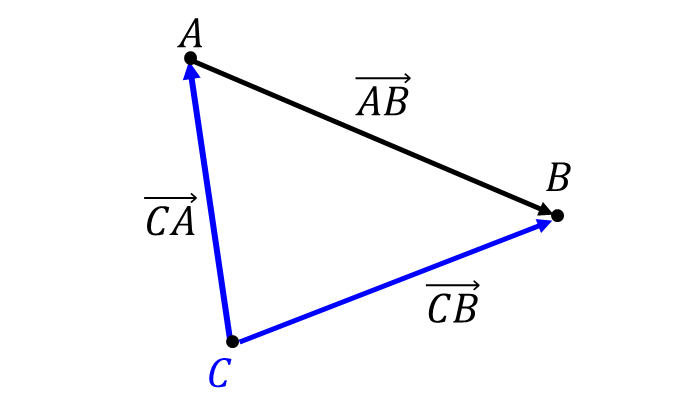
例えば、\(\overrightarrow{AB}\hspace{2pt}\)を点\(\hspace{2pt}C\hspace{2pt}\)を基準に分解すると、以下の図のように\(\hspace{2pt}\overrightarrow{AB}\hspace{2pt}\)は\(\hspace{2pt}\overrightarrow{CB}\hspace{2pt}\)から\(\hspace{2pt}\overrightarrow{CA}\hspace{2pt}\)を引いたベクトルとなることから
$${\overrightarrow{AB} = \overrightarrow{CB} - \overrightarrow{C A}}$$
となります。
差の式をそのまま覚えようとすると記号の順番を間違いやすいです。
上図から式の意味を理解して覚えるか、もしくは以下のように和の式を利用して導くという手もあります。
\begin{eqnarray}
\overrightarrow{AB} && = - \overrightarrow{BA} \\[0.3em]
&& = -(\overrightarrow{BC} + \overrightarrow{CA}) \\[0.3em]
&& = - \overrightarrow{BC} - \overrightarrow{CA} \\[0.3em]
&& = \overrightarrow{CB} - \overrightarrow{CA} \\[0.3em]
\end{eqnarray}
3.ベクトルの分解の問題
ベクトルの分解に関連した問題を解説します。
問題1 | 実数s,tを求める問題
【答え】
\(\displaystyle \vec{p} = 3 \hspace{1pt}\vec{a} + \hspace{1pt}\vec{b}\)
【解答】
$${(\hspace{1pt}4\hspace{1pt},\hspace{1pt}2) = s \hspace{1pt}(\hspace{1pt}1\hspace{1pt},\hspace{1pt}1) + t \hspace{1pt}(\hspace{1pt}1\hspace{1pt},\hspace{1pt}-1)}$$
を満たす実数\(\hspace{2pt}s\hspace{1pt},\hspace{1pt} t\hspace{2pt}\)を求めればよいので、以下の連立方程式を解きます。
\begin{cases}
4 = s+t \\[0.5em]
2 = s -t \\
\end{cases}
この連立方程式の解は\(\hspace{2pt}s = 3 \hspace{1pt},\hspace{1pt}t = 1\hspace{2pt}\)となります。
したがって
$$ \vec{p} = 3 \hspace{1pt}\vec{a} + \hspace{1pt}\vec{b} $$
と求められます。
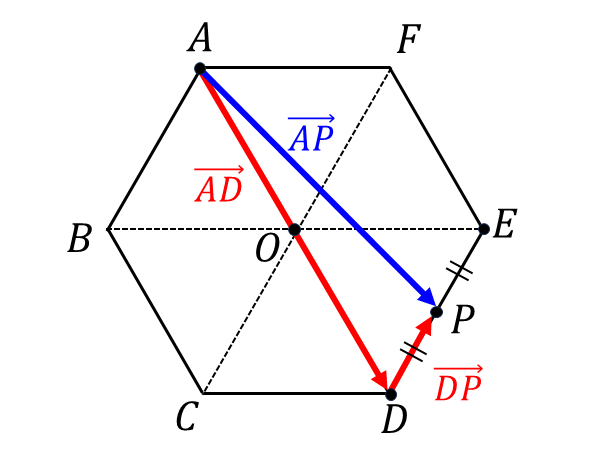
問題2 | 正六角形の問題
(1) \(\hspace{1pt} \overrightarrow{AE}\)
(2) \(\hspace{1pt} \overrightarrow{FE}\)
(3) \(\hspace{1pt} \overrightarrow{AP}\)
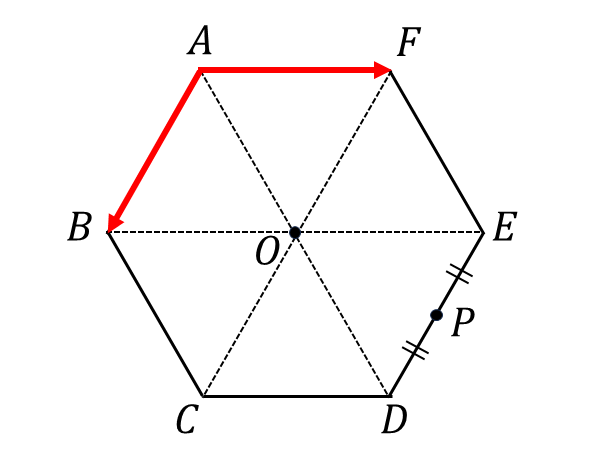
【答え】
(1) \(\displaystyle \overrightarrow{AE} = \overrightarrow{AB} + 2\hspace{1pt}\overrightarrow{AF}\)
(2) \(\displaystyle \overrightarrow{FE} = \overrightarrow{AB} + \overrightarrow{AF}\)
(3) \(\displaystyle \overrightarrow{AP} = \frac{3}{2}\overrightarrow{AB} + 2\hspace{1pt} \hspace{1pt}\overrightarrow{AF}\)
【解答のポイント】
ベクトルの分解の公式
$${\overrightarrow{AB} = \overrightarrow{A\square} + \overrightarrow{\square B}}$$
$${\overrightarrow{AB} = \overrightarrow{\square B} - \overrightarrow{\square A}}$$
から問題のベクトルを変形します。
また、正六角形の性質を利用し、向きと大きさの等しい辺でのベクトルを等号で結ぶことができます。例えば、\(\overrightarrow{AB}\hspace{2pt}\)は以下のベクトルと等しくなります。
$${\overrightarrow{AB} = \overrightarrow{FO}= \overrightarrow{OC} = \overrightarrow{ED}}$$
【(1)の解答】
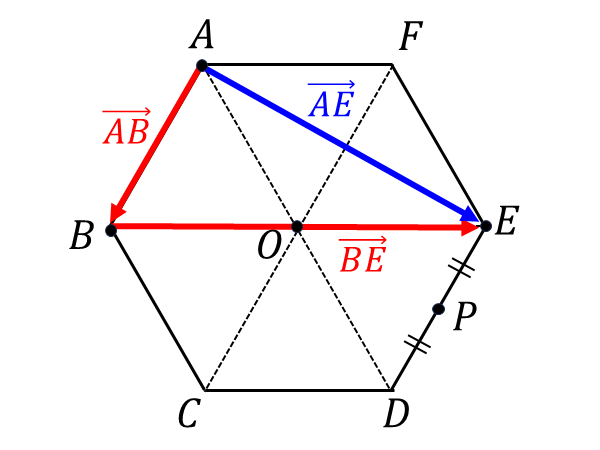
\( \overrightarrow{AE}\hspace{2pt}\)は、和の式から点\(\hspace{1pt}B\hspace{2pt}\)を経由するように変形します。また、正六角形の性質から\(\hspace{1pt}\overrightarrow{BE}=2\hspace{1pt}\overrightarrow{AF}\hspace{2pt}\)であることを利用します。
\begin{eqnarray}
\overrightarrow{AE} && = \overrightarrow{AB} + \overrightarrow{BE}\\[0.3em]
&& = \overrightarrow{AB} + 2\hspace{1pt}\overrightarrow{AF}\\[0.3em]
\end{eqnarray}
【(2)の解答】
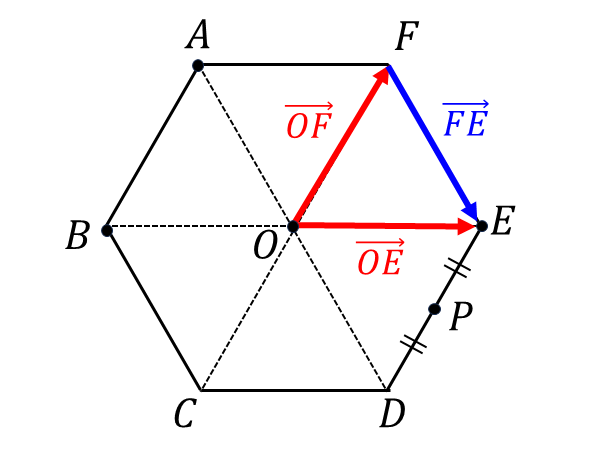
\( \overrightarrow{FE}\hspace{2pt}\)は、点\(\hspace{1pt}O\hspace{2pt}\)を基準にして差の式で変形します。
\begin{eqnarray}
\overrightarrow{FE} && = \overrightarrow{OE} - \overrightarrow{OF}\\[0.3em]
&& = \overrightarrow{AF} - (\hspace{1pt}-\overrightarrow{AB})\\[0.3em]
&& = \overrightarrow{AB} + \overrightarrow{AF} \\[0.3em]
\end{eqnarray}
【(3)の解答】
まず、\(\overrightarrow{AP}\hspace{2pt}\)は点\(\hspace{1pt}D\hspace{2pt}\)を経由する和の式で表します。また、式変形の途中に出てくる\(\hspace{2pt}\overrightarrow{AO}\hspace{2pt}\)は点\(\hspace{1pt}B\hspace{2pt}\)を経由する和の式で分解します。
\begin{eqnarray}
\overrightarrow{AP} && = \overrightarrow{AD} + \overrightarrow{DP}\\[0.3em]
&& = 2 \overrightarrow{AO} + \frac{1}{2}\hspace{1pt}\overrightarrow{DE}\\[0.3em]
&& = 2 (\overrightarrow{AB} + \overrightarrow{BO}) - \frac{1}{2}\hspace{1pt}\overrightarrow{AB}\\[0.3em]
&& = 2 (\overrightarrow{AB} + \overrightarrow{AF}) - \frac{1}{2}\hspace{1pt}\overrightarrow{AB}\\[0.3em]
&& = \frac{3}{2}\overrightarrow{AB} +2 \hspace{1pt}\overrightarrow{AF} \\[0.3em]
\end{eqnarray}