三角形の重心の位置ベクトル
本項では以下の内容を解説します。
- ・三角形の重心の位置ベクトル
- ・公式の導出
- ・例題
【1】三角形の重心の位置ベクトル
三角形の各頂点と辺の中点を結ぶ\(\hspace{1pt}3\hspace{2pt}\)本の線分が交わる点を三角形の重心といいます。
以下の図に三角形\(ABC\hspace{2pt}\)における重心\(\hspace{1pt}G\hspace{2pt}\)を示します。
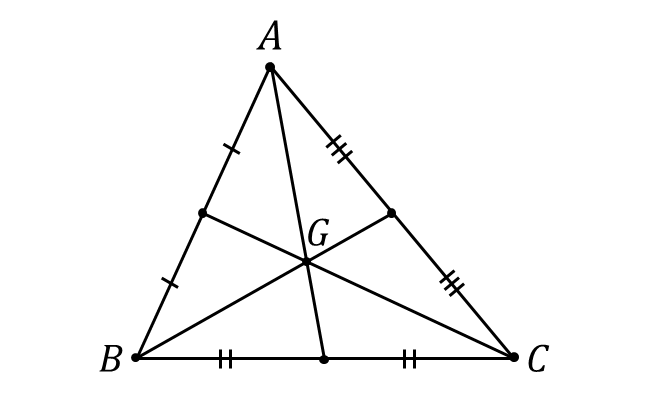
この三角形の重心\(\hspace{1pt}G\hspace{2pt}\)の位置ベクトル\(\hspace{2pt}\vec{g}\hspace{2pt}\)を各頂点の位置ベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{1pt},\hspace{1pt}\vec{c}\hspace{2pt}\)で表すと以下のようになります。
【2】三角形の重心の位置ベクトルの公式の導出
以下の図のような点\(\hspace{1pt}A\hspace{2pt}\)\((\vec{a})\hspace{1pt},\hspace{2pt}\)点\(\hspace{1pt}B\hspace{2pt}\)\((\vec{b})\hspace{1pt},\hspace{2pt}\)点\(\hspace{1pt}C\hspace{2pt}\)\((\vec{c})\hspace{2pt}\)を頂点とする三角形の重心\(\hspace{1pt}G\hspace{2pt}\)の位置ベクトル\(\hspace{2pt}\vec{g}\hspace{2pt}\)を求めます。
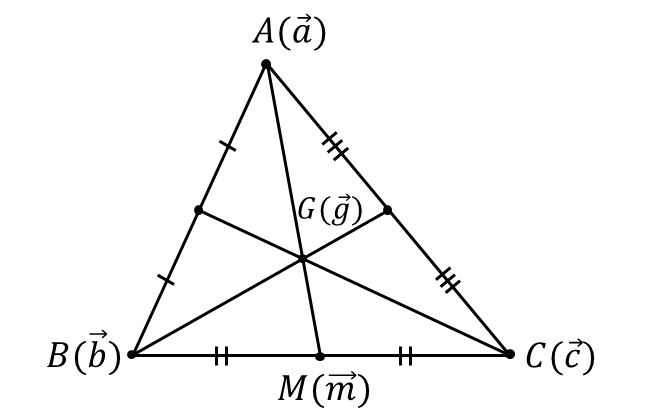
三角形の重心の位置ベクトルを求めるために、以下のベクトルの内分点の公式を用います。
辺\(\hspace{1pt}BC\hspace{2pt}\)の中点を\(\hspace{1pt}M\hspace{2pt}\)とすると、内分点の公式から位置ベクトル\(\hspace{1pt}\vec{m}\hspace{2pt}\)は $${\vec{m} = \frac{ \vec{b}+ \vec{c}}{2}}$$ となります。
ここで、重心\(\hspace{1pt}G\hspace{2pt}\)は中線\(\hspace{1pt}AM\hspace{2pt}\)を\(\hspace{2pt}2 : 1\hspace{2pt}\)に内分する点であることから \begin{eqnarray} \vec{g} = && \frac{\vec{a} + 2\hspace{1pt}\vec{m} }{2+1} \\[0.3em] = && \frac{\vec{a} + 2\hspace{1pt}\left( \frac{ \vec{b}+ \vec{c}}{2}\right)}{3} \\[0.3em] = && \frac{\vec{a} + \vec{b}+ \vec{c}}{3} \\[0.3em] \end{eqnarray} と求められます。
【3】三角形の重心の位置ベクトルの例題
三角形の重心の位置ベクトルの例題を解説します。
例題
【解答のポイント】
三角形の重心の位置ベクトルを求める公式
$${\vec{g} = \frac{\vec{a}+ \vec{b} + \vec{c}}{3}}$$
から計算します。
また、線分\(AB\hspace{2pt}\)を\(\hspace{2pt}m : n\hspace{2pt}\)に内分する点\(\hspace{1pt}P\hspace{2pt}\)の位置ベクトル\(\hspace{1pt}\vec{p}\hspace{2pt}\)を求める内分点の公式
$${\vec{p} = \frac{n \hspace{1pt} \vec{a}+ m \hspace{1pt}\vec{b}}{m+n}}$$
も使います。
【解答】
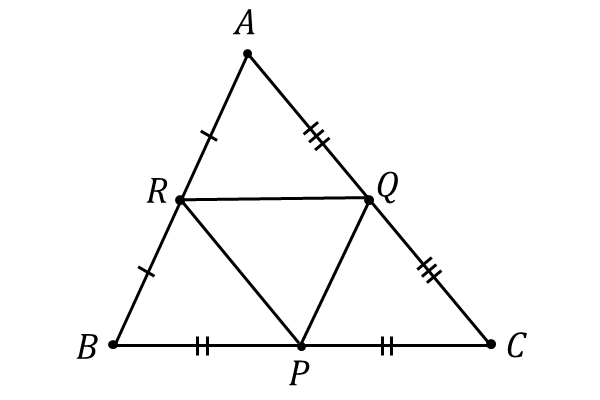
頂点\(\hspace{1pt}A\hspace{1pt},B\hspace{1pt},C\hspace{1pt}\hspace{1pt}\)および各辺の中点\(\hspace{1pt}P\hspace{1pt},Q\hspace{1pt},R\hspace{1pt}\hspace{1pt}\)の位置ベクトルをそれぞれ\(\hspace{2pt}\vec{a}\hspace{2pt},\hspace{1pt}\vec{b}\hspace{2pt},\hspace{1pt}\vec{c}\hspace{2pt},\hspace{1pt}\vec{p}\hspace{2pt},\hspace{1pt}\vec{q}\hspace{2pt},\hspace{1pt}\vec{r}\hspace{2pt}\)とします。
また、三角形\(ABC\hspace{2pt}\)の重心\(G_1\hspace{2pt}\)の位置ベクトルを\(\hspace{2pt}\vec{g_{1}}\hspace{2pt}\)、三角形\(PQR\hspace{2pt}\)の重心\(G_2\hspace{2pt}\)の位置ベクトルを\(\hspace{2pt}\vec{g_{2}}\hspace{2pt}\)とします。
三角形の重心の位置ベクトルの公式から、\(\vec{g_{1}}\hspace{2pt}\)は $${\vec{g_1} = \frac{\vec{a}+ \vec{b} + \vec{c}}{3}}$$ となります。
また、\(\vec{p}\hspace{2pt},\hspace{1pt}\vec{q}\hspace{2pt},\hspace{1pt}\vec{r}\hspace{2pt}\)は各辺の中点の位置ベクトルであるため、内分点の公式から \begin{eqnarray} \vec{p} = && \frac{\vec{b} + \vec{c} }{2} \\[0.3em] \vec{q} = && \frac{\vec{a} + \vec{c} }{2} \\[0.3em] \vec{r} = && \frac{\vec{a} + \vec{b} }{2} \\[0.3em] \end{eqnarray} となります。
三角形の重心の位置ベクトルの公式から、\(\vec{g_{2}}\hspace{2pt}\)を求めると \begin{eqnarray} \vec{g_2} = && \frac{\vec{p} + \vec{q} + \vec{r}}{3} \\[0.3em] = && \frac{1}{3} \left( \frac{\vec{b} + \vec{c} }{2} + \frac{\vec{a} + \vec{c} }{2} + \frac{\vec{a} + \vec{b} }{2}\right) \\[0.3em] = && \frac{\vec{a}+ \vec{b} + \vec{c}}{3}\\[0.3em] \end{eqnarray} となります。
すなわち、\(\vec{g_1} = \vec{g_2}\hspace{2pt}\)であることから、三角形\(ABC\hspace{2pt}\)の重心\(G_1\hspace{2pt}\)と三角形\(PQR\hspace{2pt}\)の重心\(G_2\hspace{2pt}\)は一致します。