2直線の交点のベクトル
2直線の交点のベクトルを求める問題の解き方について解説します。
【1】前提知識(ベクトルの分解)
ある任意のベクトル\(\hspace{1pt}\vec{p}\hspace{2pt}\)を平行でない\(\hspace{2pt}2\hspace{2pt}\)つのベクトル\(\hspace{2pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{2pt}\)で表すことをベクトルの分解といいます。
上記のベクトルの分解の性質から、任意のベクトル\(\hspace{1pt}\vec{p}\hspace{2pt}\)を \[ \begin{cases} \vec{p} = s \hspace{1pt} \vec{a}+ t \hspace{1pt}\vec{b} \\ \vec{p} = s\hspace{1pt}'\hspace{1pt} \vec{a}+ t\hspace{1pt}'\hspace{1pt}\vec{b} \\ \end{cases} \] と表したとき $${s = s\hspace{1pt}' \hspace{2pt},\hspace{2pt}t = t\hspace{1pt}'}$$ が成り立ちます。
この性質を利用する問題として『\(\hspace{1pt}2\hspace{2pt}\)直線の交点のベクトルを求める問題』が有名です。
\(2\hspace{2pt}\)直線の交点のベクトルをベクトルの内分点の公式によって\(\hspace{1pt}2\hspace{2pt}\)通りの方法で表し、係数を比較することで交点のベクトルを求めます。
【2】2直線の交点のベクトルを求める問題
2直線の交点のベクトルの問題を解説します。
問題1は最も典型的な『三角形の頂点と辺を内分する点を結んだ直線の交点のベクトル』を求める問題です。
【2-1】問題1
\(\hspace{1pt}\overrightarrow{OA} = \vec{a}\hspace{2pt},\hspace{2pt}\overrightarrow{OB} = \vec{b}\hspace{2pt}\)とするとき、\(\overrightarrow{OP}\hspace{2pt}\)を\(\hspace{1pt}\vec{a}\hspace{1pt},\hspace{2pt} \vec{b}\hspace{2pt}\)により表せ。
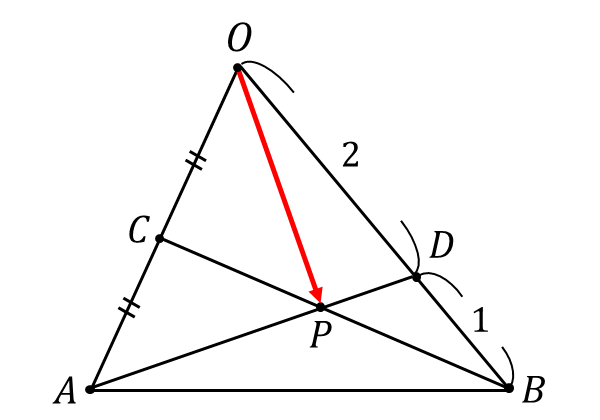
【答え】
\(\displaystyle\hspace{1pt}\overrightarrow{OP} =\frac{1}{4}\vec{a}+ \frac{1}{2}\vec{b}\)
【解答のポイント】
\(2\hspace{2pt}\)直線の交点のベクトル\(\hspace{1pt}\overrightarrow{OP}\hspace{2pt}\)を\(\hspace{1pt}2\hspace{2pt}\)通りの方法で表し、係数を比較する方法で解きます。
点\(P\hspace{2pt}\)が線分\(AD\hspace{2pt}\)を\(\hspace{2pt}AP : PD = s : 1-s\hspace{2pt}\)、線分\(BC\hspace{2pt}\)を\(\hspace{2pt}BP : PC = t : 1-t\hspace{2pt}\)と内分すると考えて、\(\overrightarrow{OP}\hspace{2pt}\)を表す式を\(\hspace{1pt}2\hspace{2pt}\)つ作ります。
\(\overrightarrow{OP}\hspace{2pt}\)を表す式は以下のベクトルの内分点の公式を用います。
【解答】
以下の図のように\(\hspace{2pt}AP : PD = s : 1-s\hspace{2pt},\)\(\hspace{2pt}BP : PC = t : 1-t\hspace{2pt}\)とします。
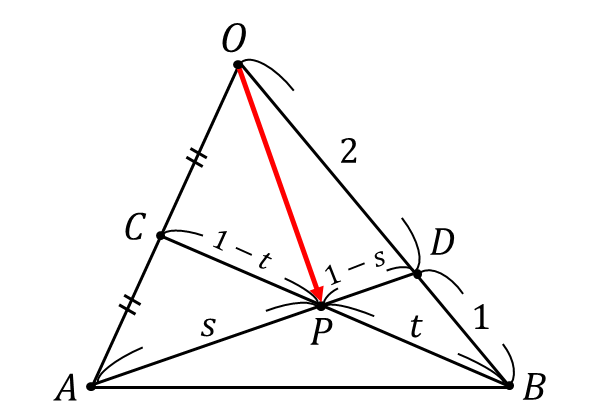
内分点の公式から、点\(P\hspace{2pt}\)が線分\(AD\hspace{2pt}\)を\(\hspace{2pt}AP : PD = s : 1-s\hspace{2pt}\)に内分することから
\begin{eqnarray}
\overrightarrow{OP} = && \frac{(1-s)\hspace{1pt}\overrightarrow{OA} + s \hspace{1pt}\overrightarrow{OD}}{s + (1-s)} \\[0.3em]
= && (1-s)\hspace{1pt}\vec{a} + s \times\left(\frac{2}{3} \hspace{1pt}\vec{b}\right) \\[0.3em]
= && (1-s)\hspace{1pt}\vec{a} +\frac{2}{3} s\hspace{1pt}\vec{b} \cdots (1)\\[0.3em]
\end{eqnarray}
また、点\(P\hspace{2pt}\)が線分\(BC\hspace{2pt}\)を\(\hspace{2pt}BP : PC = t : 1-t\hspace{2pt}\)に内分することから \begin{eqnarray} \overrightarrow{OP} = && \frac{t\hspace{1pt}\overrightarrow{OC} + (1-t) \hspace{1pt}\overrightarrow{OB}}{t + (1-t)} \\[0.3em] = && t \times \frac{1}{2}\hspace{1pt}\vec{a} + (1-t)\hspace{1pt} \vec{b} \\[0.3em] = && \frac{1}{2}t\hspace{1pt}\vec{a} +(1-t)\hspace{1pt}\vec{b} \cdots (2)\\[0.3em] \end{eqnarray}
(1)と(2)から
ここで、\(\vec{a} \neq \vec{0}\hspace{1pt},\hspace{2pt}\vec{b} \neq \vec{0}\hspace{3pt}\)かつ\(\hspace{3pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{3pt}\)は平行でないことから \begin{eqnarray} 1-s = && \frac{1}{2}t \\[0.3em] \frac{2}{3} s = && 1-t \\[0.3em] \end{eqnarray}
これを解くと $${s = \frac{3}{4}\hspace{1pt},\hspace{1pt}t = \frac{1}{2}}$$ となります。
したがって、求める\(\hspace{1pt}\overrightarrow{OP}\hspace{2pt}\)は $${\overrightarrow{OP} =\frac{1}{4}\vec{a}+ \frac{1}{2}\vec{b}}$$ となります。
【2-2】問題2
問題2は『三角形の頂点と辺\(\hspace{1pt}OA\)、辺\(\hspace{1pt}OA\hspace{2pt}\hspace{1pt}\)を外分する点を結んだ直線の交点のベクトル』を求める問題です。
\(\hspace{1pt}\overrightarrow{OA} = \vec{a}\hspace{2pt},\hspace{2pt}\overrightarrow{OB} = \vec{b}\hspace{2pt}\)とするとき、\(\overrightarrow{OP}\hspace{2pt}\)を\(\hspace{1pt}\vec{a}\hspace{1pt},\hspace{2pt} \vec{b}\hspace{2pt}\)により表せ。
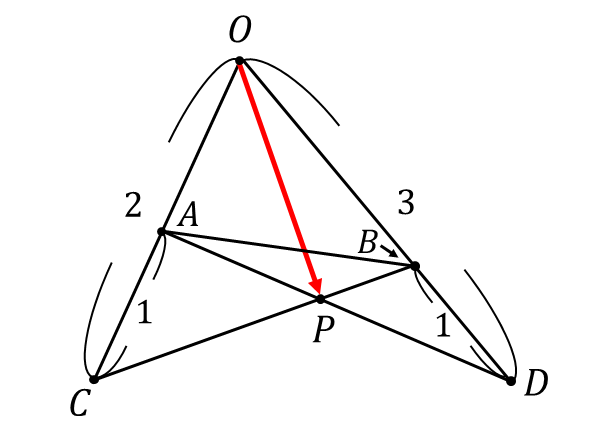
【答え】
\(\displaystyle\hspace{1pt}\overrightarrow{OP} =\frac{1}{2}\vec{a}+ \frac{3}{4}\vec{b}\)
【解答のポイント】
前問と同様に、\(2\hspace{2pt}\)直線の交点のベクトル\(\hspace{1pt}\overrightarrow{OP}\hspace{2pt}\)を\(\hspace{1pt}2\hspace{2pt}\)通りの方法で表し、係数を比較する方法で解きます。
点\(P\hspace{2pt}\)が線分\(AD\hspace{2pt}\)を\(\hspace{2pt}AP : PD = s : 1-s\hspace{2pt}\)、線分\(BC\hspace{2pt}\)を\(\hspace{2pt}BP : PC = t : 1-t\hspace{2pt}\)と内分すると考えて、\(\overrightarrow{OP}\hspace{2pt}\)を表す式を\(\hspace{1pt}2\hspace{2pt}\)つ作ります。
\(\overrightarrow{OP}\hspace{2pt}\)を表す式は以下のベクトルの内分点の公式を用います。
【解答】
以下の図のように\(\hspace{2pt}AP : PD = s : 1-s\hspace{2pt},\)\(\hspace{2pt}BP : PC = t : 1-t\hspace{2pt}\)とします。
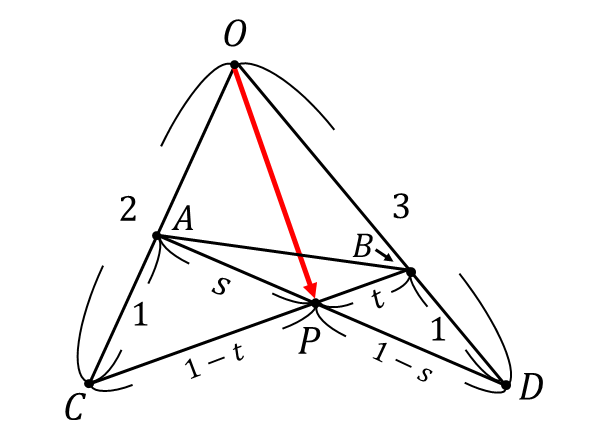
内分点の公式から、点\(P\hspace{2pt}\)が線分\(AD\hspace{2pt}\)を\(\hspace{2pt}AP : PD = s : 1-s\hspace{2pt}\)に内分することから
\begin{eqnarray}
\overrightarrow{OP} = && \frac{(1-s)\hspace{1pt}\overrightarrow{OA} + s \hspace{1pt}\overrightarrow{OD}}{s + (1-s)} \\[0.3em]
= && (1-s)\hspace{1pt}\vec{a} + s \times\left(\frac{3}{2} \hspace{1pt}\vec{b}\right) \\[0.3em]
= && (1-s)\hspace{1pt}\vec{a} +\frac{3}{2} s\hspace{1pt}\vec{b} \cdots (1)\\[0.3em]
\end{eqnarray}
また、点\(P\hspace{2pt}\)が線分\(BC\hspace{2pt}\)を\(\hspace{2pt}BP : PC = t : 1-t\hspace{2pt}\)に内分することから \begin{eqnarray} \overrightarrow{OP} = && \frac{t\hspace{1pt}\overrightarrow{OC} + (1-t) \hspace{1pt}\overrightarrow{OB}}{t + (1-t)} \\[0.3em] = && t \times 2\hspace{1pt}\vec{a} + (1-t)\hspace{1pt} \vec{b} \\[0.3em] = && 2\hspace{1pt}t\hspace{1pt}\vec{a} +(1-t)\hspace{1pt}\vec{b} \cdots (2)\\[0.3em] \end{eqnarray}
(1)と(2)から
ここで、\(\vec{a} \neq \vec{0}\hspace{1pt},\hspace{2pt}\vec{b} \neq \vec{0}\hspace{3pt}\)かつ\(\hspace{3pt}\vec{a}\hspace{1pt},\hspace{1pt}\vec{b}\hspace{3pt}\)は平行でないことから \begin{eqnarray} 1-s = && 2\hspace{1pt}t \\[0.3em] \frac{3}{2} s = && 1-t \\[0.3em] \end{eqnarray}
これを解くと $${s = \frac{1}{2}\hspace{1pt},\hspace{1pt}t = \frac{1}{4}}$$ となります。
したがって、求める\(\hspace{1pt}\overrightarrow{OP}\hspace{2pt}\)は $${\overrightarrow{OP} =\frac{1}{2}\vec{a}+ \frac{3}{4}\vec{b}}$$ となります。