単位円と三角関数の定義

本項では以下の内容を解説しています。

• ・単位円とは
• ・三角関数の定義, 値の一覧
• ・三角関数の値を求める練習問題

【1】単位円と三角関数の定義

三角比の定義では、三角比は直角三角形で定義されていたため、\(\large{0° < \theta < 90°}\) の範囲でのみ扱っていました。
また、鈍角の角度に対応するため、直角三角形の代わりに \(\large{xy}\)座標で三角比を定義することで、 \(\large{0° \leqq \theta \leqq 180°}\) の角度に三角比を拡張をしました。

三角形の角度の計算であれば \(\large{0° \leqq \theta \leqq 180°}\) の範囲で十分でしたが、三角比を関数として扱う場合は、任意の角度\(\large{\theta}\) について定義する必要があります。

そこで、単位円という半径が1の円を導入し、単位円の円周上の座標を利用して、三角関数を定義します。
本章では、単位円と三角関数の定義について解説します。

【1-1】単位円とは

単位円とは、半径が1の円のことをいいます。

下図のように、単位円を図示するときは、\(\large{xy}\)座標の原点\(\large{O}\) が中心となるように半径1の円を描きます。

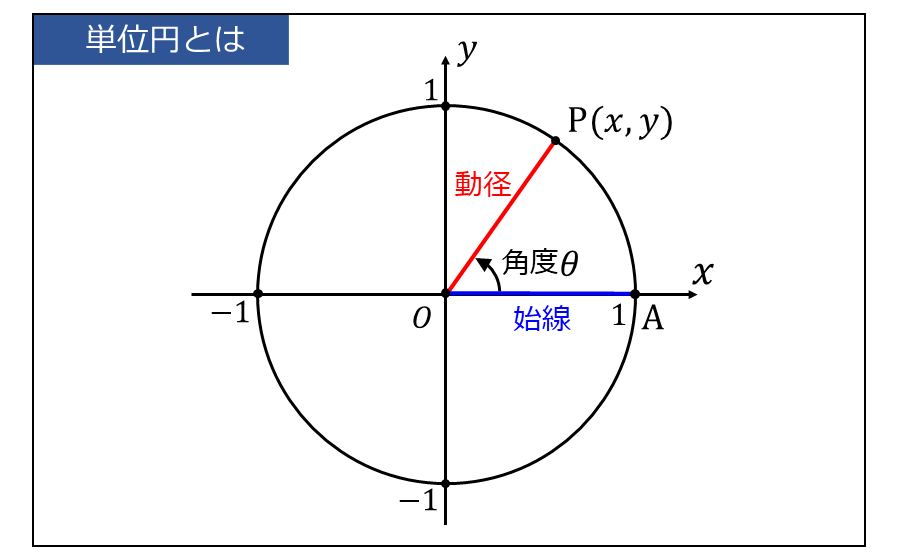
単位円と \(\large{x}\)軸の正の交点を 点\(\large{A}\) とします。また、単位円上に点\(\large{P(x,y)}\)をとります。

このとき、原点\(\large{O}\)と点\(\large{A}\)からなる線分\(\large{\overline{OA}}\) を始線といいます。また、原点\(\large{O}\) から 点\(\large{P}\)の線分 \(\large{\overline{OP}}\) を動径といいます。

この始線から動径までを反時計回りに計った角度を、正の角度\(\large{\theta}\) と定義します。
また、始線に対して時計回りに計った角度を負の角度\(\large{\theta}\) と定義します。

【1-2】単位円と三角関数

ここで、単位円における角度\(\large{\theta}\) を持つ三角形\(\large{POH}\)を描きます。
単位円上の点\(\large{P}\) から \(\large{x}\)軸に下した垂線の足を 点\(\large{H}\) とします。

三角比の定義から、角度\(\large{\theta}\) に対する \(\large{\sin \theta}\) と \(\large{\cos \theta}\) を求めます。

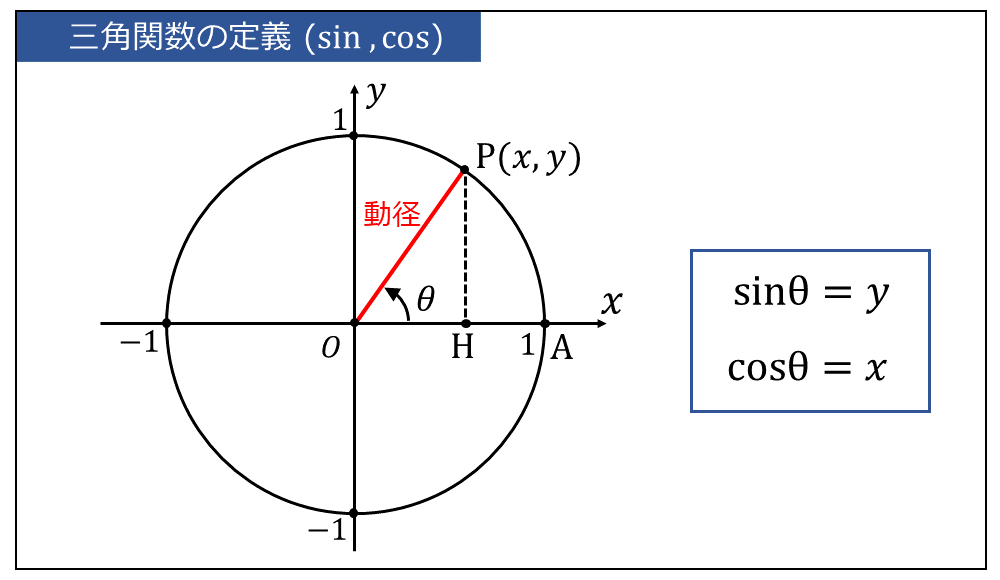
単位円は半径1の円であるため、図のように単位円に描かれた三角形は、斜辺の大きさが1の三角形となります。すなわち、 $$\large{\sin \theta =\frac{\overline{PH}}{\overline{OP}}= \frac{y}{1} = y}$$ $$\large{\cos \theta =\frac{\overline{OH}}{\overline{OP}}= \frac{x}{1} = x}$$ となります。

よって、単位円上の点\(\large{P(x,y)}\)は \(\large{y}\)座標が \(\large{\sin \theta}\)、\(\large{x}\)座標が \(\large{\cos \theta}\) となります。

【1-3】単位円とタンジェントの定義

次に、単位円における正接(タンジェント)について解説します。

下図のように \(\large{x=1}\) と動径\(\large{\overline{OP}}\) を延長した交点を \(\large{Q(1,m)}\) とします。
このとき、図中に黄色で示している三角形\(\large{QOA}\)に着目します。

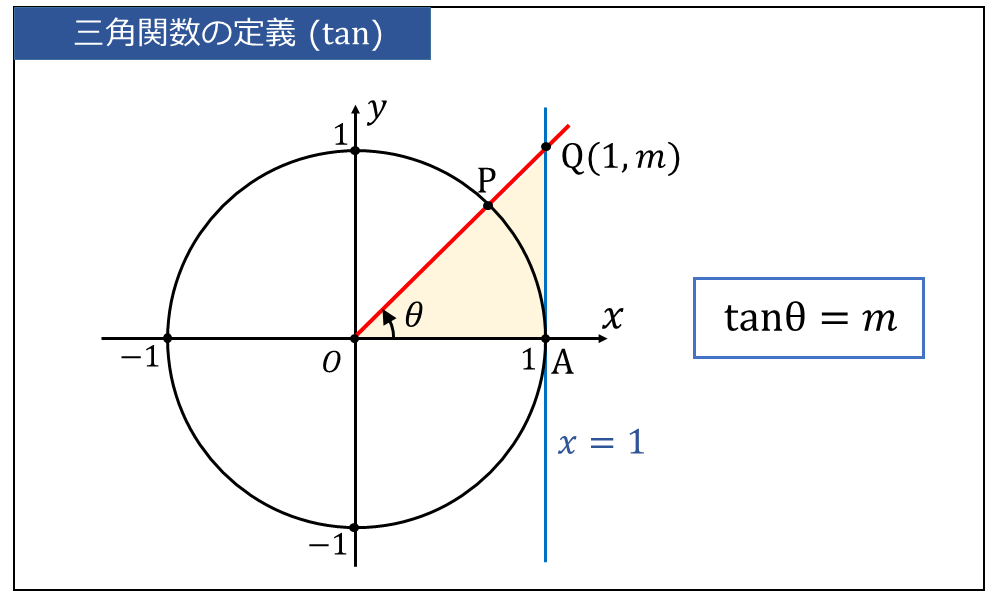
三角比の定義から、角度\(\large{\theta}\) をもつ三角形\(\large{QOA}\)のタンジェントは $$\large{\tan \theta =\frac{\overline{QA}}{\overline{OA}}= m}$$ となります。

このように、単位円におけるタンジェントは、動径\(\large{\overline{OP}}\)を延長し、\(\large{x=1}\)との交わる点\(\large{Q}\) の \(\large{y}\)座標と定義することができます。

動径\(\large{\overline{OP}}\)を直線の方程式で記述すると、\(\large{y=mx}\) となります。つまり、\(\large{m}\) とは動径\(\large{\overline{OP}}\) を式で表した時の直線の傾きを表しています。

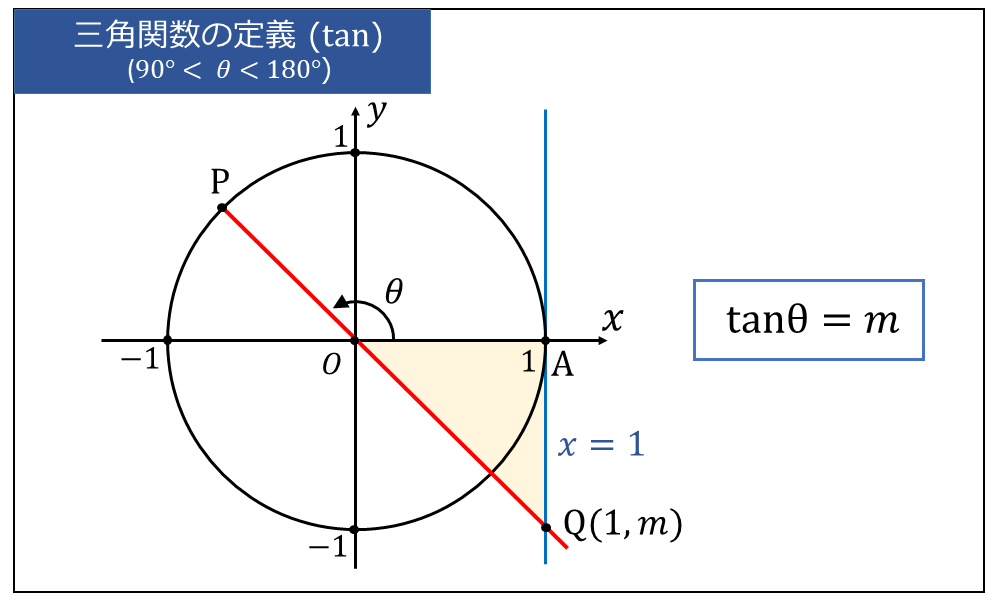
また、角度\(\large{\theta}\)が \(\large{90°< \theta < 180°}\) の場合は、以下の図のように、動径を延長し、\(\large{x=1}\) との交わる点の \(\large{y}\)座標から定義できます。

\(\large{\tan \theta}\) は、\(\large{\sin \theta}\) と \(\large{\cos \theta}\) に対して $$\displaystyle \large{\tan \theta = \frac{\sin \theta}{\cos \theta}}$$ の関係があるため、点\(\large{P(x,y)}\) の座標を使用して、 $$\displaystyle \large{\tan \theta = \frac{y}{x}}$$ と考えても、間違いではありません。しかし、この定義では \(\large{\tan \theta}\) の値や符号を考えるときに、\(\large{\sin \theta}\)、\(\large{\cos \theta}\) の値を経由して考える必要があります。

一方、\(\large{\tan \theta = m}\) の定義では、\(\large{\tan \theta}\) を直接に定義することができます。また、『\(\large{\tan \theta}\) は動径の傾きである』と考えることで、\(\large{\tan \theta}\) の符号が直観的に分かりやすくなります。

・タンジェントが定義されない角度

ここで、角度 \(\large{\theta = 90°}\) では、\(\large{x=1}\) の直線と交わらなくなるため、\(\large{\tan \theta}\) は定義されません。
\(\large{\tan \theta}\) の定義されない角度は、\(\large{180°}\) ごとに存在します。整数を\(\large{n}\)とすると $$\large{\theta = 90°+180°\times n}$$ (もしくは、\(\large{\theta = \frac{1}{2}\pi+n\pi}\)) において \(\large{\tan \theta}\) が定義されません。

三角関数 \(\large{y=\tan \theta}\) のグラフでは、この定義されない角度の位置に漸近線を持ちます。
(三角関数のグラフについては別ページで解説しています。)

【2】単位円と弧度法による角度

三角関数に使用する角度には、弧度法が使用されます。

弧度法とは、角度を 『円の半径』と『円弧の長さ』の比により表す表記方法です。(詳しくは、弧度法で解説しています。)

弧度法では、円の一周分の角度を \(\large{2 \pi}\) とします。したがって、\(\large{2 \pi = 360°}\) となります。
また、円の4分の1にあたる直角 \(\large{90°}\) は、\(\displaystyle \large{\frac{\pi}{2}}\) となります。

同様に、\(\displaystyle \large{\frac{1}{6}\pi = 30°}\)、\(\displaystyle \large{\frac{1}{4}\pi = 45°}\)、\(\displaystyle \large{\frac{1}{3}\pi = 60°}\) となります。

弧度法による角度を、単位円上にまとめた図を示します。三角関数の値や符号を考えるときに、単位円上の位置を覚えておくと便利です。

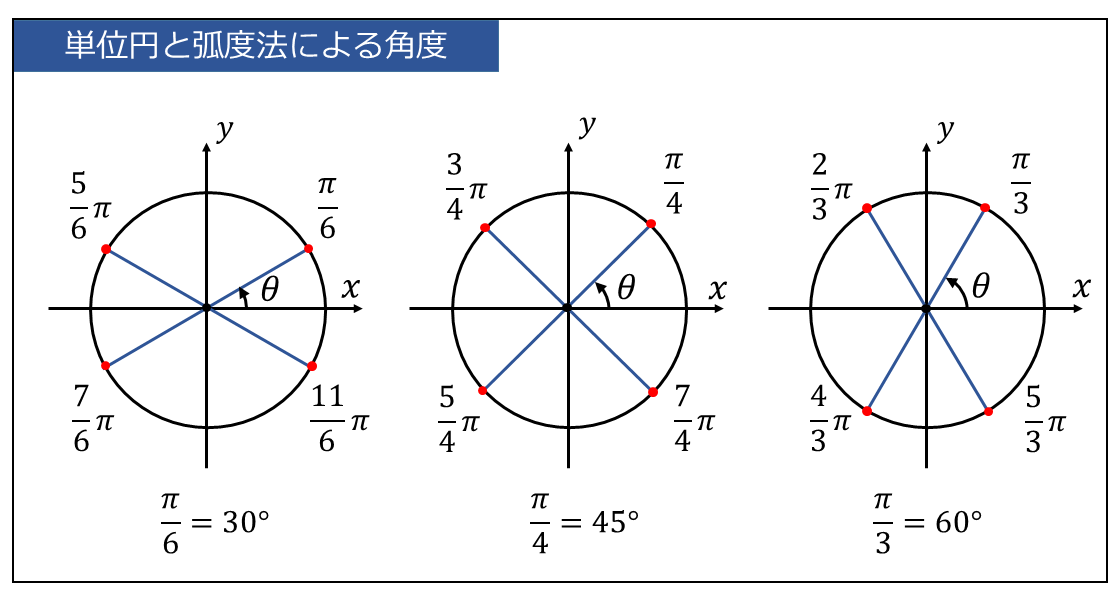
また、以下に度数法[°] と 弧度法[rad] の一覧表を示します。

【3】三角関数の値の求め方

本章では、三角関数の基本となる \(\large{0° \leqq \theta \leqq 360°}\) の範囲で代表的な三角関数の値について解説します。

三角関数の値は、象限ごとに符号が変化する点がややこしいですが
 『三角関数の定義』と『単位円上の角度の位置関係』
を考えることで各象限の三角関数の値を わかりやすく求めることができます。

・sinの値の求め方

角度 \(\displaystyle \large{\theta = \frac{\pi}{6},\hspace{2pt}\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)の4つの角度に対応する \(\large{\sin \theta}\) の値について考えます。

第1章の三角関数の定義から、\(\large{\sin \theta}\) は 単位円上の点\(\large{P(x,y)}\)の \(\large{y}\) 座標の値、すなわち $$\large{\sin \theta = y}$$ となります。

ここで、\(\displaystyle \large{\theta = \frac{\pi}{6},\hspace{2pt}\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)を単位円上に図示します。

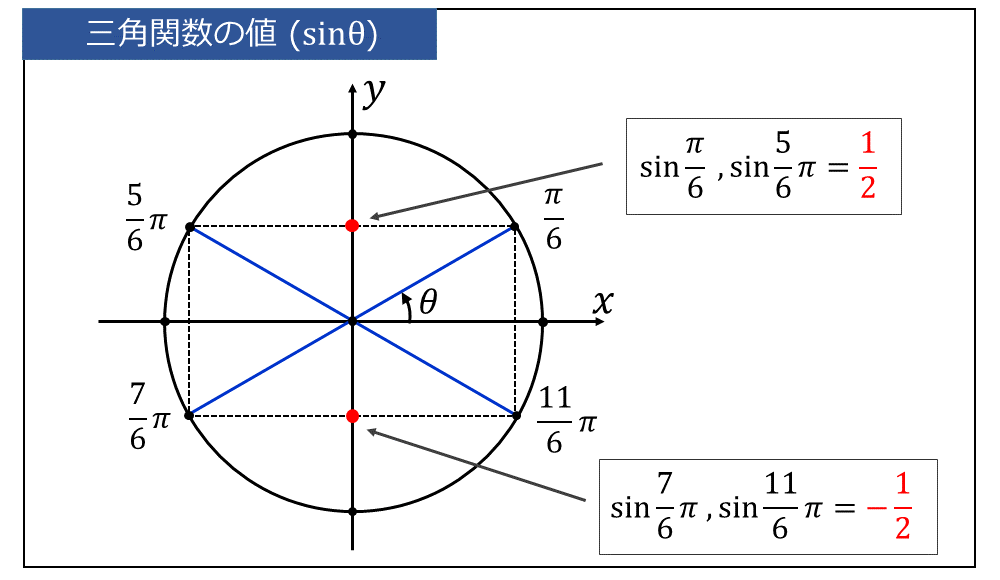
まず、弧度法の\(\large{\displaystyle \hspace{2pt} \frac{\pi}{6}}\) は\(\large{\hspace{2pt}30°\hspace{2pt}}\)の大きさの角度を表します。
つまり、角度\(\displaystyle \large{\frac{\pi}{6}}\)の三角比は、30°の角度をもつ直角三角形における三角比と同じであり、 $$\large{\sin \frac{\pi}{6} = \frac{1}{2}}$$ となります。

残りの \(\displaystyle \large{\theta =\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\) の \(\large{\sin \theta}\) の値は、単位円上の \(\large{\displaystyle\frac{\pi}{6}}\) との位置関係により求めることができます。

上図より角度\(\large{\displaystyle \frac{5}{6} \pi}\) は角度\(\large{\displaystyle \frac{\pi}{6}}\) と 単位円上で\(\large{\color{red}{y}}\)軸に関して対称な位置にあります。
\(\large{\sin \theta}\) は 単位円の \(\large{y}\)座標の値に等しいため、\(\displaystyle \large{\sin \frac{\pi}{6}}\) と \(\large{\displaystyle \sin \frac{5}{6} \pi}\) は同じ値を持ちます。 $$\large{\sin \frac{\pi}{6} = \sin \frac{5}{6}\pi = \frac{1}{2}}$$

一方、上図から角度\(\large{\displaystyle \frac{7}{6} \pi, \hspace{2pt} \frac{11}{6} \pi}\) は \(\large{\displaystyle \frac{\pi}{6},\hspace{2pt} \frac{5}{6}\pi}\) と 単位円上で\(\large{\color{blue}{x}}\)軸に関して対称な位置にあります。

\(\large{\sin \theta}\) は 単位円の \(\large{y}\)座標の値に等しいため、 \(\large{\displaystyle \sin \frac{\pi}{6}}\) の符号を反転させて、 $$\large{\sin \frac{7}{6}\pi = \sin \frac{11}{6}\pi = -\frac{1}{2}}$$ となります。

・cosの値の求め方

\(\displaystyle \large{\theta = \frac{\pi}{6},\hspace{2pt}\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)の4つの \(\large{\cos \theta}\) の値について考えます。

第1章の三角関数の定義から、\(\large{\cos \theta}\) は 単位円上の点\(\large{P(x,y)}\) の \(\large{x}\) 座標の値、すなわち $$\large{\cos \theta = x}$$ となります。

角度\(\displaystyle \large{\frac{\pi}{6}}\)の三角比は、30°の角度をもつ直角三角形における三角比と同じであり、 $$\large{\cos \frac{\pi}{6} = \frac{\sqrt{3}}{2}}$$ となります。

ここで、\(\displaystyle \large{\theta = \frac{\pi}{6},\hspace{2pt}\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)を単位円上に図示します。

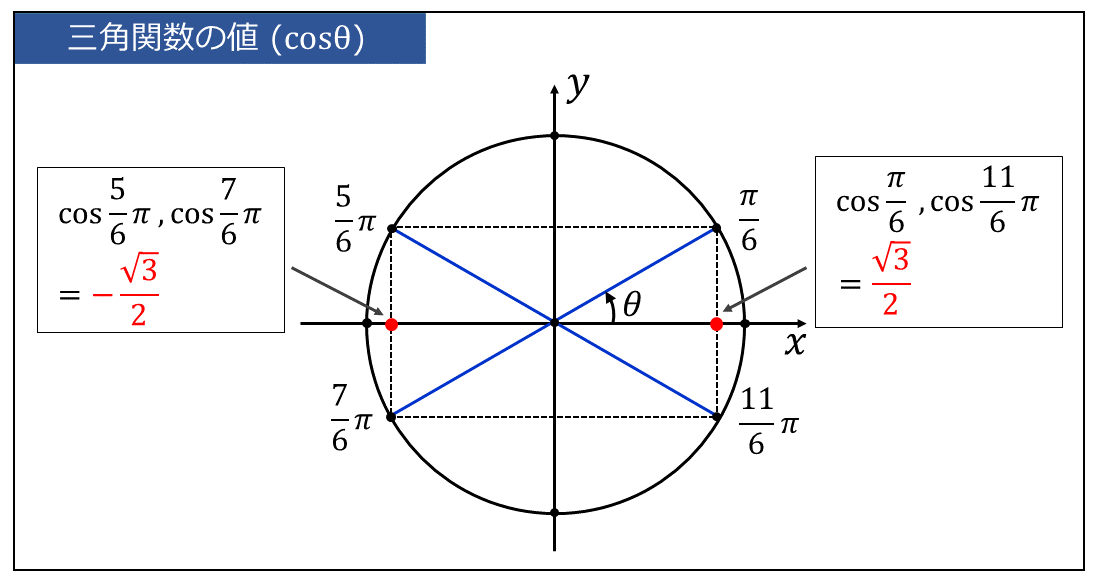
単位円上の \(\large{\displaystyle\frac{\pi}{6}}\) との位置関係により、残りの \(\displaystyle \large{\theta =\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)の \(\large{\cos \theta}\) の値を考えます。

上図から角度\(\large{\displaystyle \frac{11}{6} \pi}\) は \(\large{\displaystyle \frac{\pi}{6}}\) と 単位円上で\(\large{\color{blue}{x}}\)軸に関して対称な位置にあります。

ここで、\(\large{\cos \theta}\) は 単位円の \(\large{x}\)座標の値に等しいため、角度\(\large{\displaystyle \frac{11}{6} \pi}\) は、角度\(\large{\displaystyle \frac{\pi}{6}}\) と同じ値を持つため、 $$\large{\cos \frac{11}{6}\pi = \cos \frac{\pi}{6} = \frac{\sqrt{3}}{2}}$$ となります。

また、上図から、角度\(\large{\displaystyle \frac{5}{6} \pi}\)、\(\large{\displaystyle \frac{7}{6} \pi}\) は角度\(\large{\displaystyle \frac{\pi}{6}}\)、\(\large{\displaystyle \frac{11}{6} \pi}\) と 単位円上で\(\large{\color{red}{y}}\)軸に関して対称な位置にあります。

ここで、\(\large{\cos \theta}\) は 単位円の \(\large{x}\)座標の値に等しいため、\(\displaystyle \large{\cos \frac{5}{6}\pi}\) と \(\large{\displaystyle \cos \frac{7}{6} \pi}\)は、 \(\displaystyle \large{\cos \frac{\pi}{6}}\) の符号を反転した関係にあります。 $$\large{\cos \frac{5}{6}\pi = \cos \frac{7}{6}\pi = -\frac{\sqrt{3}}{2}}$$

・tanの値の求め方

\(\displaystyle \large{\theta = \frac{\pi}{6},\hspace{2pt}\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)の4つの角度の \(\large{\tan \theta}\) の値について考えます。

第1章の三角関数の定義から、\(\large{\tan \theta}\) は 単位円の動径を延長した線と、\(\large{x=1}\)との交点\(\large{Q(1,m)}\)の \(\large{y}\) 座標の値であり、 $$\large{\tan \theta = m}$$ となります。

ここで、角度\(\displaystyle \large{\frac{\pi}{6}}\)の \(\large{\tan \theta}\) は、角度30°の直角三角形の三角比となるため、 $$\large{\tan \frac{\pi}{6} = \frac{1}{\sqrt{3}}}$$ となります。

\(\displaystyle \large{\theta = \frac{\pi}{6},\hspace{2pt}\frac{5}{6}\pi,\hspace{2pt}\frac{7}{6}\pi,\hspace{2pt}\frac{11}{6}\pi\hspace{2pt}}\)を単位円上に図示します。

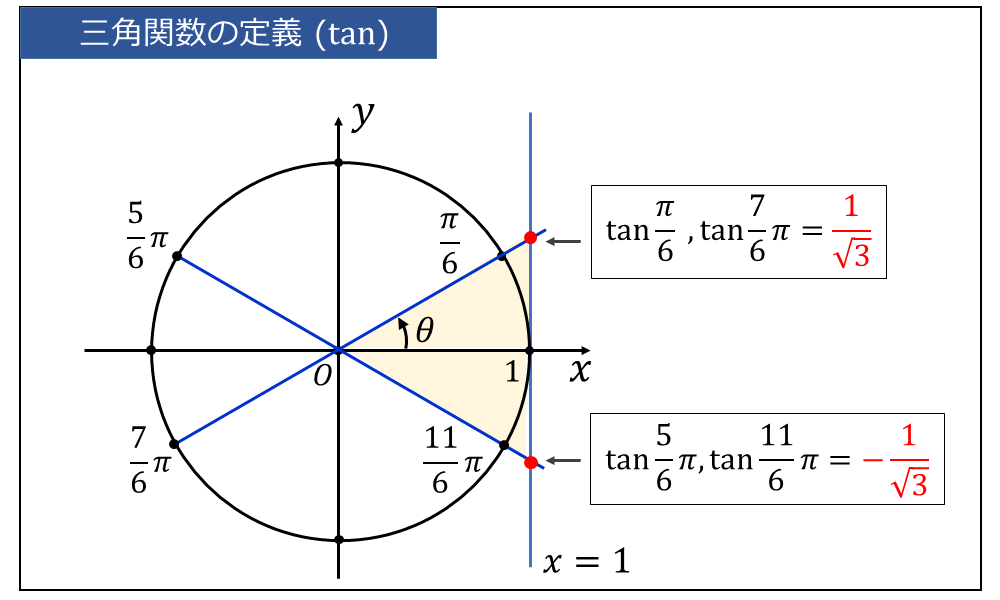
上図に示すように、\(\displaystyle \large{\tan \frac{7}{6} \pi}\) は、\(\large{\displaystyle \tan \frac{\pi}{6}}\)と交点の\(\large{y}\)座標が一致するため、同じ値となります。したがって、 $$\large{\tan \frac{\pi}{6} =\tan \frac{7}{6} \pi = \frac{1}{\sqrt{3}}}$$ となります。

また、\(\displaystyle \large{\tan \frac{5}{6} \pi}\)、\(\displaystyle \large{\tan \frac{11}{6} \pi}\) は、\(\displaystyle \large{\frac{\pi}{6}}\) のときの交点の \(\large{y}\)座標の値と \(\large{x}\)軸に関して対称な位置となります。 つまり、 $$\large{\tan \frac{5}{6}\pi =\tan \frac{11}{6} \pi = -\frac{1}{\sqrt{3}}}$$ となります。

三角関数の値の一覧

三角関数の \(\large{0° \leqq \theta \leqq 360°}\) における代表的な値を以下の表にまとめます。

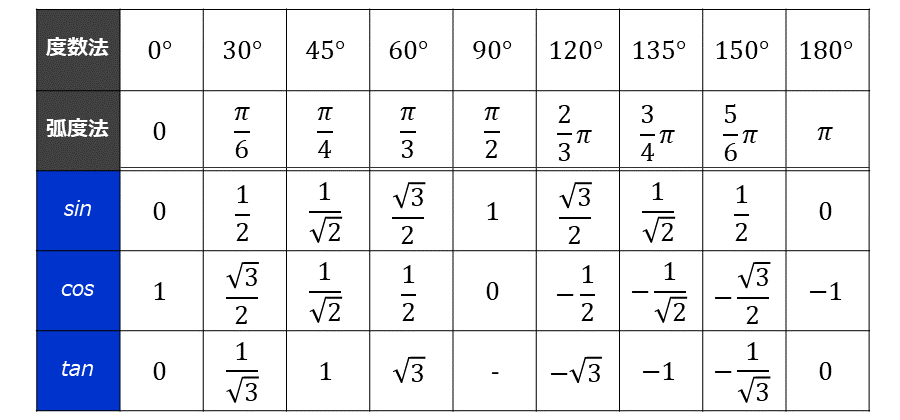
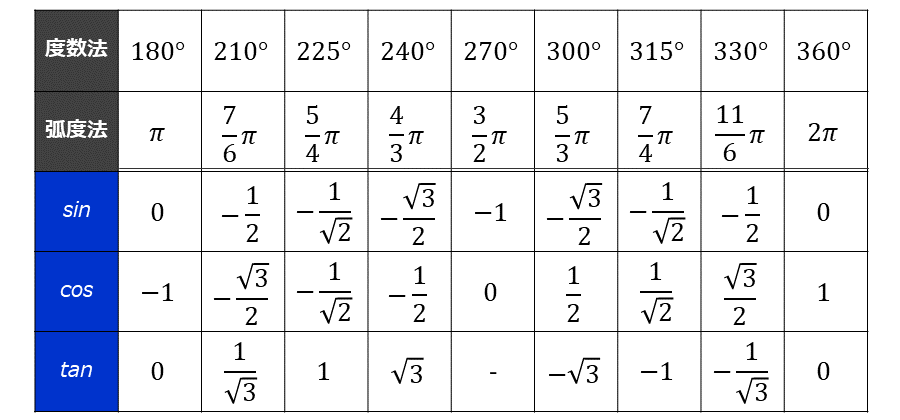
単位円は、\(\large{2 \pi \hspace{1pt}(360°)}\) だけ角度が異なると、一周回転し、動径の位置が一致します。

したがって、\(\large{2 \pi}\) の整数倍だけ角度が異なる場合は、その三角関数の値も同じ値になります。
つまり、\(\large{n}\)を整数とすると、 $$\large{\sin (\theta + 2 n \pi) = \sin \theta}$$ $$\large{\cos (\theta + 2 n \pi) = \cos \theta}$$ $$\large{\tan (\theta + 2 n \pi) = \tan \theta}$$ が成り立ちます。

例えば、\(\displaystyle \large{\theta = \frac{9}{4} \pi}\) のとき、 $$\large{\frac{9}{4} \pi = \frac{1}{4} \pi + 2 \pi}$$ であるから、 $$\large{\sin \frac{9}{4}\pi = \sin \frac{1}{4}\pi = \frac{1}{\sqrt{2}}}$$ と求めることができます。

上記に、三角関数の \(\large{0° \leqq \theta \leqq 360°}\) の一覧を示しましたが、角度\(\large{\theta}\) が負のときや、\(\large{360°}\) を超える範囲では、『表中の角度から \(\large{2 \pi}\) の整数倍だけずれている』と考え、表中の値に変換して三角関数の値を求めることができます。

三角関数の符号の一覧

三角関数はその角度の象限の位置によって、決まった符号を持ちます。
以下に三角関数の各象限における符号を図示します。

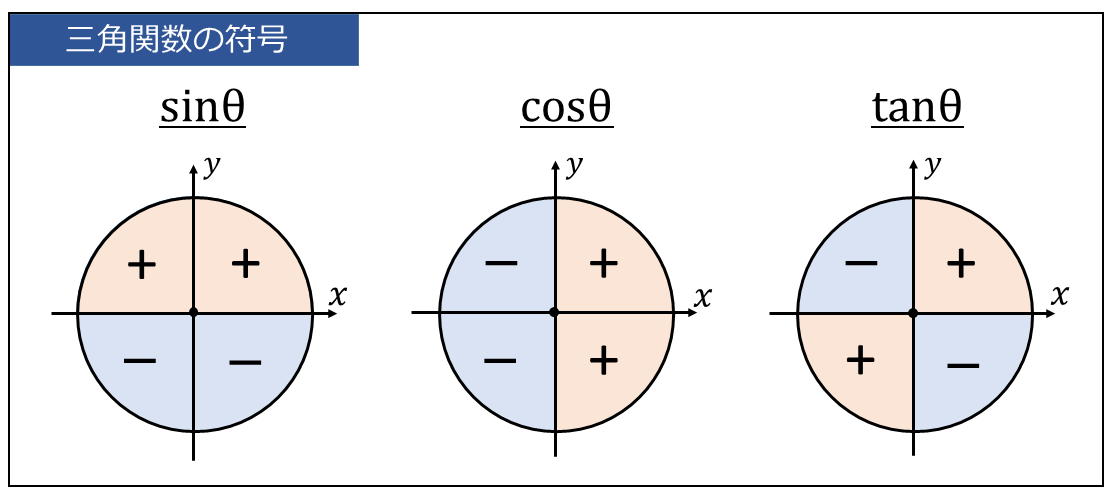
【4】三角関数の値を求める問題

本章では、三角関数の値の問題について解説します。

【4-1】角度からsin,cos,tanを求める問題

【解答と解説】
$$\displaystyle \large{\frac{7}{3}\pi = \frac{1}{3}\pi + 2\pi}$$ であるため、\(\displaystyle \large{\frac{7}{3}\pi}\) の三角関数は、\(\displaystyle \large{\frac{1}{3}\pi}\) の三角関数の値と等しくなります。

つまり、 $$\displaystyle \large{\sin \frac{7}{3}\pi = \frac{\sqrt{3}}{2}}$$ $$\displaystyle \large{\cos \frac{7}{3}\pi = \frac{1}{2}}$$ $$\displaystyle \large{\tan \frac{7}{3}\pi = \sqrt{3}}$$ となります。

【4-2】負の角度のsin,cos,tanを求める問題

【解答と解説】
$$\displaystyle \large{-\frac{1}{4}\pi = \frac{7}{4}\pi - 2\pi}$$ であるため、\(\displaystyle \large{-\frac{1}{4}\pi}\) の三角関数は、\(\displaystyle \large{\frac{7}{4}\pi}\) の三角関数の値と等しくなります。

角度が \(\large{\displaystyle \large{\frac{7}{4}\pi}}\) のとき、\(\large{\cos \theta}\) は正の値、\(\large{\sin \theta}\) と \(\large{\tan \theta}\) は負の値となります。

以上から、 $$\displaystyle \large{\sin \left(-\frac{1}{4}\pi \right) = -\frac{1}{\sqrt{2}}}$$ $$\displaystyle \large{\cos \left(-\frac{1}{4}\pi \right) = \frac{1}{\sqrt{2}}}$$ $$\displaystyle \large{\tan \left(-\frac{1}{4}\pi \right) = -1}$$ となります。

【4-3】円周率の整数倍のsin,cos,tanを求める問題

【解答と解説】
$$\displaystyle \large{3\pi = \pi + 2\pi}$$ であるため、\(\displaystyle \large{3\pi}\) の三角関数は、\(\displaystyle \large{\pi}\) の三角関数の値と等しくなります。

つまり、 $$\displaystyle \large{\sin 3\pi = 0}$$ $$\displaystyle \large{\cos 3\pi = -1}$$ $$\displaystyle \large{\tan 3\pi = 0}$$ となります。

---