三角関数の極限
本項では、『三角関数の極限』と『問題と解き方』について解説します。
【1】三角関数の極限
本章では、三角関数の極限の基本的な性質について解説します。
【1-1】sin と cos の極限
三角関数 \(\large{y=\sin x}\) と \(\large{y=\cos x}\) は \(\large{x}\) に対して \(\large{-1 \leqq y \leqq 1}\) の間を周期的に値をとります。
\(\large{y=\sin x}\) と \(\large{y=\cos x}\) のグラフは以下のようになります。
(三角関数のグラフについては別の記事に解説しています)
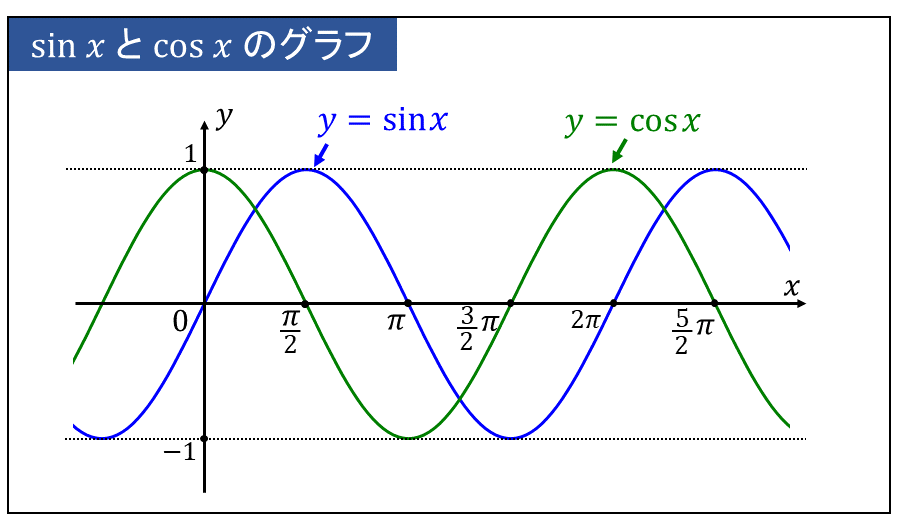
\(\large{y=\sin x}\) と \(\large{y=\cos x}\) は 周期的に値をとるため、『\(\large{x \to \infty}\)』 と 『\(\large{x \to -\infty}\)』 に極限をもちません。
【1-2】tan の極限
三角関数 \(\large{y=\tan x}\) は \(\large{x}\) に対して \(\large{-\infty \leqq y \leqq \infty}\) の範囲で周期的に値をとります。
\(\large{y=\tan x}\) のグラフは以下のようになります。
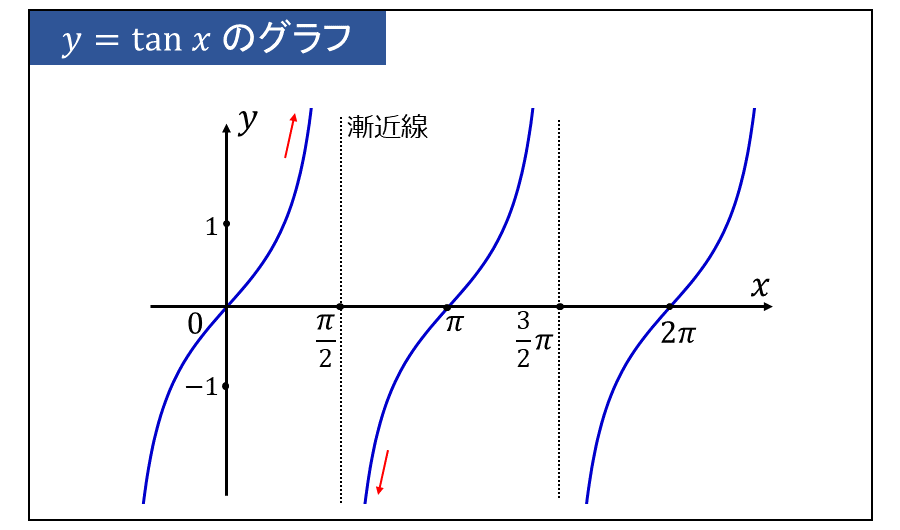
上図から分かるように、 \(\large{y=\tan x}\) は \(\displaystyle\large{x=\frac{\pi}{2}+n\pi}\) (\(\large{n}\) は整数) において漸近線をもつことから、以下が成り立ちます。
$$\large{\lim_{x \to \frac{\pi}{2}+0}\tan x = -\infty,\hspace{3pt}\lim_{x \to \frac{\pi}{2}-0}\tan x = \infty }$$
三角関数の極限についてまとめると、以下のようになります。
\(\large{x \to \infty\hspace{1pt},\hspace{4pt}}\)\(\large{x \to -\infty}\) に極限をもたない
・例題
三角関数の極限の例題を解説します。
\(\displaystyle \large{(1)\hspace{5pt}\lim_{x \to \infty} \sin \frac{1}{x}}\hspace{9pt}\)
\(\displaystyle \large{(2)\hspace{5pt}\lim_{x \to \frac{3}{2}\pi+0}\tan x }\)
例題1(1)は、変数を \(\displaystyle\large{\frac{1}{x}=t}\) と置き換えると、\(\large{x \to \infty}\) のとき \(\large{t \to 0}\) であるから、 $$\large{\lim_{x \to \infty} \sin \frac{1}{x}=\lim_{t \to 0} \sin t =0}$$ となります。
例題1(2)は、\(\large{y=\tan x}\) が \(\displaystyle\large{x=\frac{\pi}{2}+n\pi}\) (\(\large{n}\) は整数) において漸近線をもつことから、 $$\large{\lim_{x \to \frac{3}{2}\pi+0}\tan x = -\infty}$$ となります。
【2】sinx/x の極限値
本章では、三角関数の極限の計算でよく使用される極限値について解説します。
角度\(\large{x}\)の単位が 弧度法 であるとき、以下の極限が存在します。
また、上記から導かれる式として、以下のような極限値があります。
【2-1】sinx/x の極限値の証明
上記の三角関数の極限① $$\large{\lim_{x \to 0} \frac{\sin x}{x} = 1}$$ を証明します。
\(\large{x \to 0}\) であるとき、\(\large{x}\) は \(\displaystyle\large{0 < |x| < \frac{\pi}{2}}\) を満たします。
[Ⅰ]【 \(\displaystyle\large{0 < x < \frac{\pi}{2}}\) の場合】
以下のような半径\(\large{1}\)、角度\(\large{\color{blue}{x}}\) の扇形\(\large{OAB}\) について考えます。
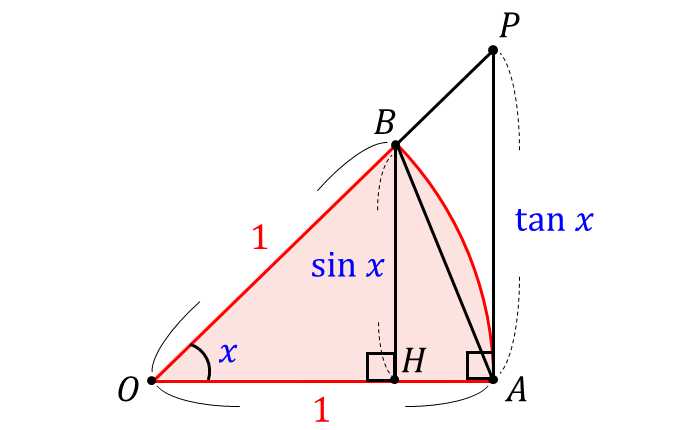
点\(\large{B}\) から \(\large{\overline{OA}}\) に下した垂線を \(\large{\overline{BH}}\) とします。
このとき、\(\large{\overline{BH}}\) の長さは \(\large{\color{blue}{\sin x}}\) となります。
また、円弧\(\large{AB}\) の 点\(\large{A}\) における接線 と、\(\large{\overline{OB}}\) を延長した線が交わる点を 点\(\large{P}\) とします。
このとき、\(\large{\overline{PA}}\) は \(\large{\overline{OA}}\) と垂直であり、\(\large{\overline{PA}}\) の長さは \(\large{\color{blue}{\tan x}}\) となります。
ここで、上図の3つの部分の面積を比較すると、
三角形\(\large{OAB}\) \(\large{<}\) 扇形\(\large{OAB}\) \(\large{<}\) 三角形\(\large{OAP}\)
となります。
それぞれの面積の大きさを計算すると、
$$\large{\frac{1}{2}\cdot\color{red}{1}\color{black}{}\cdot\color{blue}{\sin x}\color{black}{} < \frac{1}{2}\cdot\color{red}{1^2}\color{black}{}\cdot\color{blue}{x}\color{black}{} < \frac{1}{2}\cdot\color{red}{1}\color{black}{}\cdot\color{blue}{\tan x}}$$
すなわち、 $$\large{\sin x < x <\tan x}$$ 上式を \(\large{\sin x}\) で割ると、\(\large{\sin x >0}\) であることから、 $$\large{1 < \frac{x}{\sin x} <\frac{1}{\cos x}}$$ よって、逆数をとると 以下の(1)式が導かれます。 $$\large{1 > \frac{\sin x}{x} > \cos x \hspace{7pt}(1)}$$
ここで、関数の極限値の大小関係には、以下の関係が成り立ちます。
\(\large{x}\) が \(\large{a}\) に近いとき、
常に \(\large{f(x) \leqq h(x) \leqq g(x)}\) かつ \(\large{\alpha = \beta}\)
ならば \(\displaystyle\large{\lim_{x \to a}h(x) = \alpha}\)
上記の極限値の大小関係は 『はさみうちの原理』 ともいわれます。
(1)式に 極限値の大小関係 を利用すると、 $$\large{\lim_{x \to +0}\cos x = 1}$$ であることから、 $$\large{\lim_{x \to +0}\frac{\sin x}{x} = 1}$$ と求めることができます。
[Ⅱ]【 \(\displaystyle\large{-\frac{\pi}{2} < x < 0}\) の場合】
\(\large{x=-t}\) とおくと、\(\displaystyle\large{0 < t < \frac{\pi}{2}}\) となることから、
\begin{eqnarray}
\large
\lim_{x \to -0}\frac{\sin x}{x}&\large =&\large \lim_{x \to +0}\frac{\sin (-t)}{-t} \\[0.5em]
\large
&\large =&\large \lim_{x \to +0}\frac{\sin t}{t} \\[0.5em]
\large
&\large =&\large 1 \\
\end{eqnarray}
となります。
[Ⅰ]、[Ⅱ] の結果から、以下が成り立ちます。 $$\large{\lim_{x \to 0}\frac{\sin x}{x} = 1}$$
【2-2】x/sinx, tanx/x の極限値
\(\displaystyle\large{\lim_{x \to 0}\frac{\sin x}{x} = 1}\) の式を利用すると、以下の式も導出することができます。
(2)式の導出
$$\large{\lim_{x \to 0} \frac{x}{\sin x} = \lim_{x \to 0} \frac{1}{\frac{\sin x}{x}} = 1}$$
(3)式の導出
$$\large{\lim_{x \to 0} \frac{\tan x}{x} = \lim_{x \to 0} \frac{\sin x}{x}\cdot\frac{1}{\cos x} = 1}$$
・例題
三角関数の極限の例題を解説します。
\(\displaystyle \large{(1)\hspace{5pt}\lim_{x \to 0} \frac{\sin 3x}{x}}\hspace{9pt}\)
\(\displaystyle \large{(2)\hspace{5pt}\lim_{x \to \infty } x\sin \frac{1}{x} }\)
例題1(1)は、三角関数の極限 \(\displaystyle\large{\lim_{x \to 0} \frac{\sin x}{x}}\) の式が使えるように変形します。 $$\large{\lim_{x \to 0} \frac{\sin 3x}{x}=\lim_{x \to 0} \frac{\sin 3x}{3x}\cdot3 =3}$$ となります。
例題1(2)は、変数を \(\displaystyle\large{\frac{1}{x}=t}\) と置き換えると、\(\large{x \to \infty}\) のとき \(\large{t \to 0}\) であるから、 $$\large{\lim_{x \to \infty } x\sin \frac{1}{x}=\lim_{t \to 0} \frac{\sin t}{t}=1}$$ となります。
【3】問題と解き方
本章では、三角関数の極限 に関連した問題について解説します。
\(\displaystyle \large{\lim_{x \to 0} \frac{\sin x°}{x}}\)
\(\displaystyle \large{\lim_{x \to 0}\frac{\sin (\sin x)}{\sin x}}\)
\(\displaystyle \large{\lim_{x \to 0}\frac{1-\cos x}{x^2}}\)
\(\displaystyle \large{\lim_{x \to 0}\frac{\sin 2x -2\sin x}{x^3}}\)
問題1, 2, 3, 4 は 三角関数の極限 \(\displaystyle\large{\lim_{x \to 0}\frac{\sin x}{x}=1}\) に関連した問題です。
(解答と解説 : 問題1 問題2 問題3 問題4)
\(\displaystyle \large{\lim_{x \to 0}x \sin \frac{1}{x}}\)
\(\displaystyle \large{\lim_{x \to \infty}\frac{\cos^2 x}{x} }\)
問題5, 6 は 前章で利用した極限の大小関係の『はさみうちの原理』を使用する問題です。
(解答と解説 : 問題5 問題6)
問題.1 三角関数の極限
\(\displaystyle \large{\lim_{x \to 0} \frac{\sin x°}{x}}\)
【解答と解説】
問題の変数\(\large{x}\) は度数法であるため、弧度法で定義された \(\displaystyle\large{\lim_{x \to 0} \frac{\sin x}{x}=1}\) をそのまま使うことはできません。
そのため、式変形によって、弧度法に変換して極限を求めます。
弧度法への変換は $$\large{1° = \frac{\pi}{180}}$$ の関係式を利用します。
\begin{eqnarray} \large \lim_{x \to 0} \frac{\sin x°}{x}&\large =&\large \lim_{x \to 0} \frac{\sin \frac{\pi}{180}x}{x} \\[0.5em] \large &\large =&\large\lim_{x \to 0} \frac{\sin \frac{\pi}{180}x}{\frac{\pi}{180} x} \cdot\frac{\pi}{180} \\[0.5em] \large &\large =&\large \frac{\pi}{180} \\ \end{eqnarray}
問題.2 三角関数の極限
\(\displaystyle \large{\lim_{x \to 0}\frac{\sin (\sin x)}{\sin x}}\)
三角関数の極限の問題ですが、式中に \(\displaystyle\large{\lim_{x \to 0} \frac{\sin x}{x}=1}\) がありません。そこで本問では、変数を置き換えることで \(\displaystyle\large{ \frac{\sin x}{x}}\) に変形します。
\(\large{\sin x = t}\) と置き換えると、\(\large{x \to 0}\) のとき \(\large{t \to 0}\) となります。
すなわち、 $$\large{\lim_{x \to 0}\frac{\sin (\sin x)}{\sin x} = \lim_{t \to 0}\frac{\sin t}{t} =1}$$
問題.3 三角関数の極限
\(\displaystyle \large{\lim_{x \to 0}\frac{1-\cos x}{x^2}}\)
三角関数の極限の問題ですが、式中に \(\displaystyle\large{\lim_{x \to 0} \frac{\sin x}{x}=1}\) がありません。この場合は、三角関数の相互関係の式 \(\large{\sin^2 x + \cos^2 x = 1}\) により \(\displaystyle\large{ \frac{\sin x}{x}}\) を作り出すようにします。
\begin{eqnarray} \large \lim_{x \to 0}\frac{1-\cos x}{x^2}&\large =&\large \lim_{x \to 0}\frac{(1-\cos x)(1+\cos x)}{x^2(1+\cos x)} \\[0.5em] \large &\large =&\large\lim_{x \to 0}\frac{1-\cos^2 x}{x^2(1+\cos x)} \\[0.5em] \large &\large =&\large\lim_{x \to 0}\frac{\sin^2 x}{x^2(1+\cos x)} \\[0.5em] \large &\large =&\large \frac{1}{2} \\ \end{eqnarray}
問題.4 三角関数の極限
\(\displaystyle \large{\lim_{x \to 0}\frac{\sin 2x -2\sin x}{x^3}}\)
三角関数の二倍角の公式 \(\large{\sin 2x = 2\sin x \cos x}\) により式を変形します。
\begin{eqnarray} \large \lim_{x \to 0}\frac{\sin 2x -2\sin x}{x^3}&\large =&\large\lim_{x \to 0}\frac{2\sin x \cos x -2\sin x}{x^3} \\[0.5em] \large &\large =&\large\lim_{x \to 0}\frac{-2\sin x(1-\cos x)}{x^3} \\[0.5em] \large &\large =&\large\lim_{x \to 0}\frac{-2\sin x(1-\cos^2 x)}{x^3(1+\cos x)} \\[0.5em] \large &\large =&\large\lim_{x \to 0}\frac{-2\sin^3 x}{x^3(1+\cos x)} \\[0.5em] \large &\large =&\large-1 \\[0.5em] \end{eqnarray}
問題.5 はさみうちの原理の利用
\(\displaystyle \large{\lim_{x \to 0}x \sin \frac{1}{x}}\)
本問は、極限の大小関係の『はさみうちの原理』を利用する問題です。
\(\large{x}\) が \(\large{a}\) に近いとき、
常に \(\large{f(x) \leqq h(x) \leqq g(x)}\) かつ \(\large{\alpha = \beta}\)
ならば \(\displaystyle\large{\lim_{x \to a}h(x) = \alpha}\)
\(\displaystyle\large{0 \leqq \left|\sin \frac{1}{x}\right| \leqq 1}\) であることから、
$$\large{0 \leqq \left|x \sin \frac{1}{x}\right| =|x| \left| \sin \frac{1}{x}\right| \leqq |x|}$$
となります。
ここで、\(\displaystyle\large{\lim_{x \to 0} |x| = 0}\) であることから、 $$\large{\lim_{x \to 0}\left|x \sin \frac{1}{x}\right| = 0}$$ したがって、 $$\large{\lim_{x \to 0}x \sin \frac{1}{x} = 0}$$ となります。
問題.6 はさみうちの原理の利用
\(\displaystyle \large{\lim_{x \to \infty}\frac{\cos^2 x}{x} }\)
問題5と同様に、極限の大小関係の『はさみうちの原理』を利用します。
\(\displaystyle\large{0 \leqq \left|\cos^2 x\right| \leqq 1}\) であることから、\(\large{x \neq 0}\) のとき
$$\large{0 \leqq \left| \frac{\cos^2 x}{x}\right| = \frac{|\cos^2 x|}{|x|} \leqq \frac{1}{|x|}}$$
となります。
ここで、\(\displaystyle\large{\lim_{x \to \infty} \frac{1}{|x|}= 0}\) であることから、 $$\large{\lim_{x \to \infty}\left| \frac{\cos^2 x}{x}\right| = 0}$$ したがって、 $$\large{\lim_{x \to \infty}\frac{\cos^2 x}{x} = 0}$$ となります。