定積分の計算

本項では、『定積分の計算』 と 『問題の解き方』について解説します。

【1】定積分の計算

関数 \(\large{f(x)}\) の不定積分を \(\large{F(x)}\) とするとき、2つの実数 \(\large{a,b}\) で定義される区間 \(\large{a \leqq x \leqq b}\) における定積分は以下のように計算されます。

上式の \(\large{a}\) を定積分の下端、\(\large{b}\) を定積分の上端といいます。

・例題 | 不定積分と定積分の違い

『不定積分』 と 『定積分』 の違いを次の例題から考えてみます。

例題(1)の不定積分は以下の公式から計算します。 $$\large{\int x^n dx = \frac{1}{n+1}x^{n+1} + C}$$ から、\(\large{n=2}\) とすると、 $$\large{\int x^2 dx = \frac{1}{3}x^{3} + C}$$ と求められます。

一方、例題(2)は 例題(1)で求められた不定積分 \(\displaystyle \large{F(x)=\frac{1}{3}x^{3} + C}\) から以下のように求められます。 \begin{eqnarray} \large \int_1^{2} x^2 dx&\large =&\large \left[ \frac{1}{3}x^{3} \right]_1^2\\[0.5em] \large &\large =&\large \frac{1}{3} \cdot 2^3 - \frac{1}{3} \cdot 1^3 \\[0.5em] \large &\large =&\large \frac{7}{3} \\ \end{eqnarray}

例題(1)の不定積分は、微分すると \(\large{x^2}\) となる関数を求める計算です。そのため、積分定数 \(\large{C}\) を式に含む 関数\(\large{F(x)+C}\) が求められます。

一方、例題(2)の定積分は、不定積分から求められた関数 \(\large{F(x)+C}\) に \(\large{x=1,2}\) の値を代入した差分 $$\large{F(2)+C-\{\hspace{1pt}F(1)+C\hspace{1pt}\} = F(2)-F(1)}$$ を計算するため、積分定数 \(\large{C}\) のない値 \(\large{F(2)-F(1)}\) が求められます。

・定積分の意味

\(\large{f(x)>0}\) であるとき、区間 \(\large{a \leqq x \leqq b}\) における定積分は、関数\(\large{f(x)}\) と 直線 \(\large{x=a}\)、\(\large{x=b}\) と \(\large{x}\)軸に囲まれた面積 \(\large{S}\) を意味します。

例えば、上記の例題(2)の定積分 $$\large{\int_1^{2} x^2 dx = \frac{7}{3}}$$ は、以下の図に示すように 区間 \(\large{1 \leqq x \leqq 2}\) における \(\large{f(x)=x^2}\) と直線 \(\large{x=a}\)、\(\large{x=b}\) と \(\large{x}\)軸に囲まれた面積 \(\large{S}\) となります。

関数 \(\large{f(x)}\) が 区間 \(\large{a \leqq x \leqq b}\) において負の場合は、定積分の値も負となります。

例えば、\(\large{f(x)=-x^2}\) であるときの定積分は $$\large{\int_1^{2} -x^2 dx = -\frac{7}{3}}$$ となります。

そのため、\(\large{f(x)}\) が負である場合も含めて \(\large{x}\)軸 と 曲線\(\large{f(x)}\) に囲まれた面積\(\large{S}\) を求める場合は、\(\large{f(x)}\) に絶対値をつけて計算します。 $$\large{S = \int_a^{b} |f(x)| dx}$$

区間 \(\large{a \leqq x \leqq b}\) で \(\large{f(x)\geqq 0}\)、区間 \(\large{b \leqq x \leqq c}\) で \(\large{f(x)\leqq 0}\) である場合、上記の絶対値を外して以下のように面積\(\large{S}\) が求められます。 $$\large{S = \int_a^{b} f(x) \hspace{1pt}dx - \int_b^{c} f(x) \hspace{1pt}dx}$$

【2】定積分の性質

関数の定数倍や和の定積分には、以下のような関係が成り立ちます。ただし、\(\large{k,l}\) は定数とします。

・例題

例えば、以下のような定積分の問題について考えます。

定積分の性質を利用して式を変形します。 \begin{eqnarray} \large \int_1^{2} ( 3x^2 + 4x ) \hspace{1pt}dx&\large =&\large 3 \int_1^{2} x^2 \hspace{1pt}dx + 4 \int_1^{2} x \hspace{1pt}dx\\[0.5em] \large &\large =&\large 3\cdot \left[ \frac{1}{3}x^{3} \right]_1^2+ 4\cdot \left[\frac{1}{2}x^{2} \right]_1^2\\[0.5em] \large &\large =&\large (2^3 - 1^3) + 2\cdot(2^2-1^2)\\[0.7em] \large &\large =&\large 13\\ \end{eqnarray} と求められます。

・定積分の性質②

また、定積分の区間 \(\large{a,b}\) に関して以下のような性質があります。

・例題

例えば、以下のような定積分の問題について考えます。

定積分の性質を利用して式を変形します。 \begin{eqnarray} \large \int_1^{4} 3x^2 dx - \int_2^{4} 3x^2 dx&\large =&\large \int_1^{4} 3x^2 dx + \int_4^{2} 3x^2 dx\\[0.5em] \large &\large =&\large \int_1^{2} 3x^2 dx\\[0.5em] \large &\large =&\large 3 \left[ \frac{1}{3}x^{3} \right]_1^2\\[0.7em] \large &\large =&\large 2^3-1^3\\[0.5em] \large &\large =&\large 7\\ \end{eqnarray} と求められます。

【3】問題と解き方

本章では、定積分の問題について解説します。

問題(1)～(3)は、基本的な定積分の計算の問題です。
(解答と解説 : 問題(1) 問題(2) 問題(3))

問題(4)は、定積分から二次関数の定数を決定する問題です。
(解答と解説 : 問題(4))

問題(5),(6)は、定積分を含む方程式から、関数を決定する問題です。
(解答と解説 : 問題(5) 問題(6))

問題(7)は、定積分の区間に 変数\(\large{x}\) が含まれている問題です。
(解答と解説 : 問題(7))

問題(1) 分数関数の定積分

【解答と解説】
本問のように分数の関数は、和に変形して積分します。

問題(2) 二次関数の定積分

【解答と解説】
本問の関数 \(\large{(x-1)(x-2)}\) のように簡単に展開できる場合は、展開して積分を計算します。

問題(3) 絶対値のついた関数の定積分

【解答と解説】
関数に絶対値が付いている場合は、絶対値を外してから積分を計算します。

問題の関数をグラフを描くと、以下のようになります。
下図の青い箇所が積分する範囲となります。

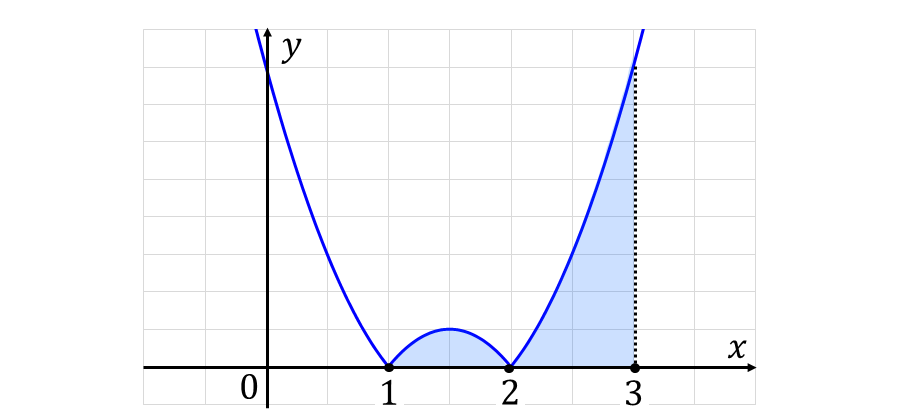
グラフを参考に絶対値を外すと、以下のように積分できます。

問題(4) 定積分から定数を求める問題

【解答と解説】
本問は、定積分の値から二次関数の定数を決定する問題です。

まず、\(\displaystyle\large{\int_0^{3} f(x)\hspace{1pt}dx= 9}\) の左辺を計算すると、以下のようになります。 \begin{eqnarray} \large \int_0^{3} f(x)\hspace{1pt}dx&\large =&\large \int_0^{3} (ax^2+bx) \hspace{1pt}dx\\[0.5em] \large &\large =&\large \left[ \frac{a}{3}x^{3} + \frac{b}{2}x^{2} \right]_0^3 \\[0.7em] \large &\large =&\large \frac{a}{3}(3^3 -0^3) +\frac{b}{2}(3^2 -0^2) \\[0.7em] \large &\large =&\large 9a +\frac{9}{2}b\\[0.7em] \end{eqnarray} すなわち、 $$\large{9a +\frac{9}{2}b = 9}$$ であることから、 $$\large{a +\frac{b}{2} = 1 \hspace{5pt}\cdots(1)}$$ となります。

また、\(\displaystyle\large{\int_0^{2} xf(x)\hspace{1pt}dx= 2}\) の左辺を計算すると、以下のようになります。 \begin{eqnarray} \large \int_0^{2} xf(x)\hspace{1pt}dx&\large =&\large \int_0^{3} (ax^3+bx^2) \hspace{1pt}dx\\[0.5em] \large &\large =&\large \left[ \frac{a}{4}x^{4} + \frac{b}{3}x^{3} \right]_0^2 \\[0.7em] \large &\large =&\large \frac{a}{4}(2^4 -0^4) +\frac{b}{3}(2^3 -0^3) \\[0.7em] \large &\large =&\large 4a +\frac{8}{3}b\\[0.7em] \end{eqnarray} すなわち、 $$\large{4a +\frac{8}{3}b = 2\hspace{5pt}\cdots(2)}$$ となります。

(1)式、(2)式から \(\large{a,b}\) の値を求めると、 $$\large{a = \frac{5}{2}\hspace{1pt},\hspace{3pt}b=-3}$$ と求められます。

問題(5) 定積分を含む方程式

【解答と解説】
本問のように、未知の関数\(\large{f(x)}\) が積分に含まれる方程式を積分方程式といいます。

式中の \(\displaystyle\large{ \int_0^{1} f(t)\hspace{1pt} dt}\) は定数となるため、 $$\large{\int_0^{1} f(t)\hspace{1pt} dt = a}$$ とおきます。

このとき、関数 \(\large{f(x)}\) は以下のようになります。 $$\large{f(x) = x^2 + 4 a}$$

上式を区間 \(\large{0 \leqq x \leqq 1}\) で積分すると、以下のようになります。 \begin{eqnarray} \large \int_0^{1} f(x)\hspace{1pt} dx&\large =&\large \int_0^{1} (x^2+4a) \hspace{1pt}dx\\[0.5em] \large &\large =&\large \left[ \frac{1}{3}x^{3} +4a x \right]_0^1\\[0.7em] \large &\large =&\large \frac{1}{3}\cdot(1^3 -0^3)+ 4a \cdot(1-0) \\[0.7em] \large &\large =&\large \frac{1}{3} + 4a\\[0.7em] \end{eqnarray}

ここで、\(\displaystyle\large{\int_0^{1} f(t)\hspace{1pt} dt = a}\) であることから、以下が成り立ちます。 $$\large{\frac{1}{3} + 4a = a}$$ すなわち、 $$\large{a = -\frac{1}{9} }$$

したがって、求める関数 \(\large{f(x)}\) は、 $$\large{f(x) = x^2 -\frac{4}{9}}$$ となります。

問題(6) 定積分を含む方程式

【解答と解説】
問題の式を変形すると、以下のようになります。 $$\large{f(x) = x^2 + x \int_0^{1} f(t)\hspace{1pt} dt + \int_0^{2} f(t)\hspace{1pt} dt}$$ 問題(4)と同様に、式中の \(\displaystyle\large{ \int_0^{1} f(t)\hspace{1pt} dt}\) と \(\displaystyle\large{\int_0^{2} f(t)\hspace{1pt} dt}\) は定数となるため、 $$\large{\int_0^{1} f(t)\hspace{1pt} dt = a}$$ $$\large{\int_0^{2} f(t)\hspace{1pt} dt = b}$$ とおきます。

このとき、関数 \(\large{f(x)}\) は以下のようになります。 $$\large{f(x) = x^2 + ax +b\hspace{10pt}\cdots(3)}$$

(3)式を区間 \(\large{0 \leqq x \leqq 1}\) で積分すると、以下のようになります。

ここで、\(\displaystyle\large{\int_0^{1} f(t)\hspace{1pt} dt = a}\) であることから、以下が成り立ちます。 $$\large{\frac{1}{3} + \frac{a}{2} + b = a}$$ すなわち、 $$\large{a = \frac{2}{3} + 2b \hspace{10pt}\cdots(4)}$$

また、(3)式を区間 \(\large{0 \leqq x \leqq 2}\) で積分すると、以下のようになります。

ここで、\(\displaystyle\large{\int_0^{2} f(t)\hspace{1pt} dt = b}\) であることから、以下が成り立ちます。 $$\large{\frac{8}{3} + 2a + 2b = b}$$ すなわち、 $$\large{b = -\frac{8}{3} -2a \hspace{10pt}\cdots(5)}$$

(4)、(5)式より、 $$\large{a = -\frac{14}{15}\hspace{1pt},\hspace{3pt}b = -\frac{4}{5}}$$

したがって、求める関数 \(\large{f(x)}\) は、 $$\large{f(x) = x^2 -\frac{14}{15}x -\frac{4}{5}}$$

問題(7) 定積分を含む方程式

【解答と解説】
本問も未知の関数\(\large{f(x)}\) が積分に含まれる方程式であり、積分方程式の問題です。

問題のように、積分区間に 変数\(\large{x}\) が含まれる場合は、両辺を \(\large{x}\) で微分することで関数\(\large{f(x)}\)を求めます。

式の左辺の不定積分の1つを \(\large{F(x)}\) とするとき、 \begin{eqnarray} \large \frac{d}{dx} \int_a^{x}f(x)\hspace{1pt} dx &\large =&\large \frac{d}{dx} \left[ F(x) \right]_a^x\\[0.5em] \large &\large =&\large \frac{d}{dx} (F(x) -F(a))\\[0.7em] \end{eqnarray} ここで、\(\large{F(x)}\) は \(\large{f(x)}\) の不定積分であるから、 $$\large{\frac{d}{dx}F(x) = f(x)}$$ また、\(\large{F(a)}\) は定数であるから、 $$\large{\frac{d}{dx}F(a) = 0}$$ すなわち、 $$\large{\frac{d}{dx} \int_a^{x}f(x)\hspace{1pt} dx = f(x)}$$ となります。

したがって、問題の両辺を \(\large{x}\) で微分すると、以下のようになります。 $$\large{f(x) = 2x}$$

また、定積分の性質から、\(\large{x=a}\) とおくと左辺が 0 となることから、 $$\large{0 = a^2 -1}$$ すなわち、 $$\large{(a+1)(a-1)=0}$$ から、 $$\large{a = \pm 1}$$ となります。

---