三角関数のグラフ
本項では以下の内容を解説しています。
- ・三角関数のグラフの特徴
- ・グラフの特徴 (定数倍,周期,平行移動)
- ・グラフを書く問題
【1】三角関数のグラフの特徴
本章では、三角関数 \(\large{y=\sin \theta}\)、\(\large{y=\cos \theta}\)、\(\large{y=\tan \theta}\) のグラフの特徴について解説します。
【1-1】sinθのグラフの特徴
下図に \(\large{y=\sin \theta}\) のグラフを示します。
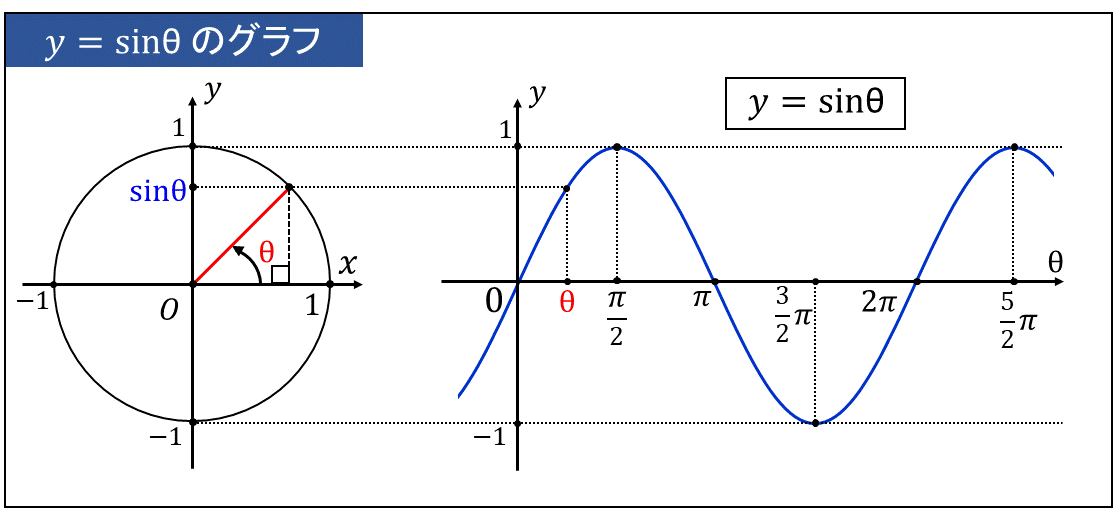
\(\large{y=\sin \theta}\) のグラフは、横軸に単位円の動径の角度\(\large{\color{red}{\theta}}\)、縦軸に\(\large{\color{blue}{\sin \theta}}\) の値を取ったグラフです。
三角関数の定義から、\(\large{\sin \theta}\) は角度\(\large{\theta}\) における単位円の \(\large{y}\) 座標を意味します。
以下に \(\large{y=\sin \theta}\) の値を \(\displaystyle \large{\frac{\pi}{2}}\) 刻みで書いた表を示します。
座標\(\large{(\theta, y)}\) の点を繋げて曲線を描いたものが \(\large{y=\sin \theta}\) のグラフとなります。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) | \(\displaystyle \large{2\pi}\) | \(\displaystyle \large{\frac{5}{2}\pi}\) | \(\displaystyle \large{3\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) |
\(\large{y=\sin \theta}\) のグラフの特徴をまとめると、以下のようになります。
(2) 周期は \(\large{2 \pi}\)
(3) 奇関数(原点に関して対称なグラフ)
(1) 値域
\(\large{\sin \theta}\) は、半径1の単位円の \(\large{y}\)座標を意味しています。
すなわち、\(\large{y=\sin \theta}\) の最大値は \(\large{y=1}\)、最小値は \(\large{y=-1}\) となります。
(2) 周期
また、動径は \(\large{2\pi(=360°)}\) で一周するため、\(\large{y=\sin \theta}\) は周期が\(\large{2\pi}\)となります。
(三角関数の周期については後述しています。)
(3) 関数の対称性
三角関数の性質から、
$$\large{\sin (-\theta) = \sin\theta}$$
が成り立ちます。
すなわち、\(\large{y=\sin \theta}\) は原点対称な関数、すなわち奇関数の性質を持ちます。
【1-2】cosθのグラフの特徴
下図に \(\large{y=\cos \theta}\) のグラフを示します。
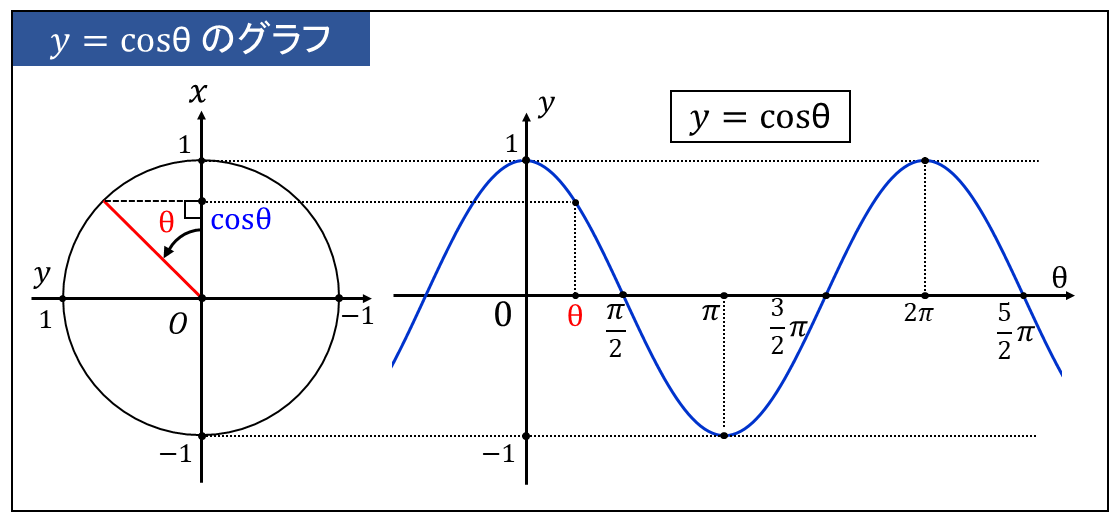
三角関数の定義から、\(\large{\cos \theta}\) は、上図の左の角度\(\large{\theta}\) における単位円の\(\large{x}\)座標を意味します。
単位円の\(\large{x}\)座標を縦軸に描くため、上図では単位円を\(\large{90°}\)回転させて描いています。
以下に \(\large{y=\cos \theta}\) の値を \(\displaystyle \large{\frac{\pi}{2}}\) 刻みで書いた表を示します。
座標\(\large{(\theta, y)}\) の点を繋げて曲線を描いたものが \(\large{y=\cos \theta}\) のグラフとなります。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) | \(\displaystyle \large{2\pi}\) | \(\displaystyle \large{\frac{5}{2}\pi}\) | \(\displaystyle \large{3\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) |
\(\large{y=\cos \theta}\) のグラフの特徴をまとめると、以下のようになります。
(2) 周期は \(\large{2 \pi}\)
(3) 偶関数(\(\large{y}\)軸に関して対称なグラフ)
(1) 値域
\(\large{\cos \theta}\) は、半径1の単位円の \(\large{x}\)座標を意味しています。
したがって、\(\large{y=\cos \theta}\) の最大値は \(\large{y=1}\)、最小値は \(\large{y=-1}\) となります。
(2) 周期
また、動径は \(\large{2\pi(=360°)}\) で一周するため、\(\large{y=\cos \theta}\) は周期が\(\large{2\pi}\)となります。
(三角関数の周期については後述しています。)
(3) 関数の対称性
三角関数の性質から、
$$\large{\cos (-\theta) = \cos\theta}$$
が成り立ちます。
すなわち、\(\large{y=\cos \theta}\) は \(\large{y}\)軸に関して対称な関数、すなわち偶関数の性質を持ちます。
【1-3】tanθのグラフの特徴
下図に \(\large{y=\tan \theta}\) のグラフを示します。
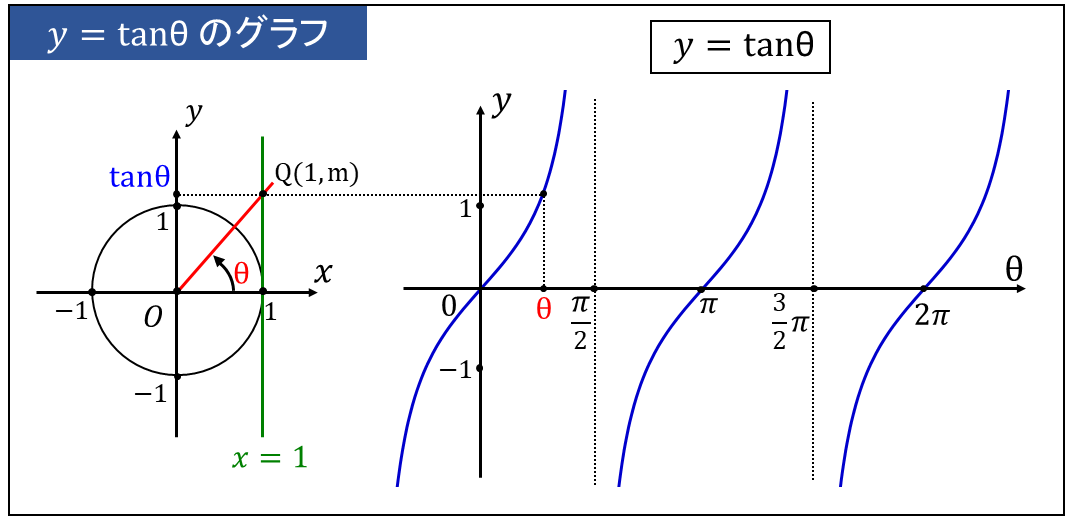
三角関数の定義から、\(\large{\tan \theta}\) は、上図の左の角度\(\large{\theta}\) における動径を延長した線と、\(\large{x=1}\) の直線の交点の \(\large{y}\)座標 \(\large{m}\) を意味します。 $$\large{\tan \theta = m}$$
以下に \(\large{y=\tan \theta}\) の値を \(\displaystyle \large{\frac{\pi}{2}}\) 刻みで書いた表を示します。
座標\(\large{(\theta, y)}\) の点を繋げて曲線を描いたものが \(\large{y=\tan \theta}\) のグラフとなります。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{-\frac{\pi}{4}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{4}}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\frac{3}{4}\pi}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{5}{4}\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | - | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | - | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | - |
\(\large{y=\tan \theta}\) のグラフの特徴をまとめると、以下のようになります。
(2) 直線 \(\displaystyle \large{\theta = \frac{\pi}{2} + n \pi}\) (\(\large{n}\)は整数) を漸近線にもつ
(3) 周期は \(\large{\pi}\)
(4) 奇関数(原点に関して対称なグラフ)
(1) 値域
\(\large{y=\tan \theta}\) のグラフは、動径の傾き \(\large{m}\) を表します。
角度 \(\displaystyle \large{-\frac{\pi}{2} < \theta < \frac{\pi}{2}}\) の範囲で考えると、\(\displaystyle \large{\theta = -\frac{\pi}{2}}\) に近づくと \(\large{-\infty}\) に発散し、\(\displaystyle \large{\theta = \frac{\pi}{2}}\) に近づくと \(\large{\infty}\) に発散します。
そのため、\(\large{y=\tan \theta}\) の値域は \(\large{-\infty \leqq y \leqq \infty}\) となります。
(2) 漸近線
また、\(\large{\theta}\) が \(\displaystyle \large{\frac{\pi}{2}}\) に近づくと、直線 \(\displaystyle \large{x= \frac{\pi}{2}}\) に限りなく近づきます。そのため、直線 \(\displaystyle \large{x= \frac{\pi}{2}}\) は \(\large{y=\tan \theta}\) の漸近線となります。
一般的には、直線 \(\displaystyle \large{\theta = \frac{\pi}{2} + n \pi}\) (\(\large{n}\)は整数) が \(\large{y=\tan \theta}\) の漸近線となります。
(3) 周期
また、動径の傾きは \(\large{\pi(=180°)}\) 回転すると一致するため、\(\large{y=\tan \theta}\) は周期が\(\large{\pi}\)となります。
(三角関数の周期については後述しています。)
(4) 関数の対称性
三角関数の性質から、
$$\large{\tan (-\theta) = -\tan\theta}$$
が成り立ちます。
すなわち、\(\large{y=\tan \theta}\) は原点に関して対称な関数、すなわち奇関数の性質を持ちます。
【2】三角関数のグラフの定数倍,周期,平行移動
本章では、三角関数のグラフを書くときに必要となる周期、平行移動、定数倍の考え方について解説します。
【2-1】定数倍
下図に \(\large{y=\sin \theta}\) と \(\large{y=2\sin \theta}\) を比較したグラフを示します。
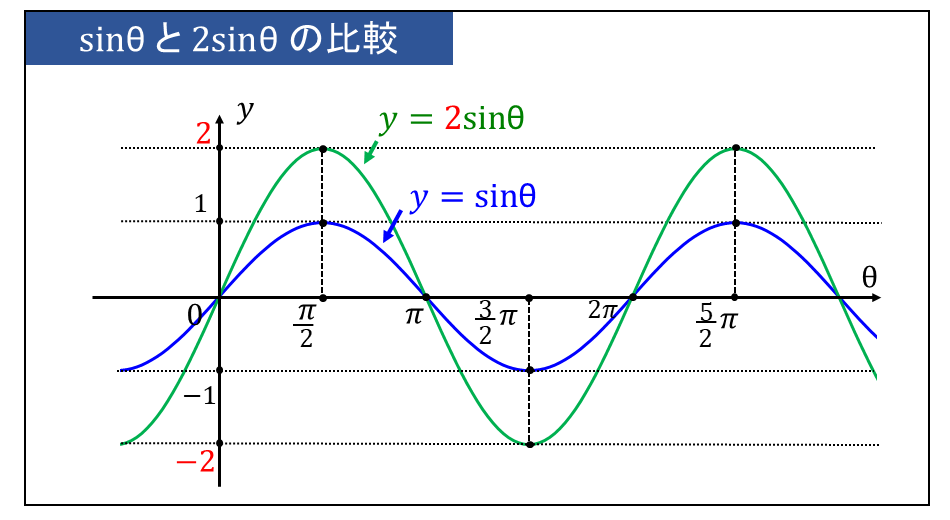
先述したように、\(\large{y=\sin \theta}\) は最大値が1,最小値が-1となります。
一方、\(\large{y=2\sin \theta}\) は全ての \(\large{\theta}\) に対する \(\large{y}\) の値が2倍されるため、最大値が2,最小値が-2 となります。
一般的には、定数 \(\large{a}\) に対して以下が成り立ちます。
【2-2】三角関数の周期
三角関数のグラフは、特定の周期で同じ形状が繰り返される という特徴を持ちます。
例えば、下図に示すように \(\large{y=\sin \theta}\) は、\(\large{2 \pi}\) の間隔で同じ形状を繰り返すグラフです。
このとき、『\(\large{y=\sin \theta}\) の周期は \(\large{2 \pi}\) である』といいます。
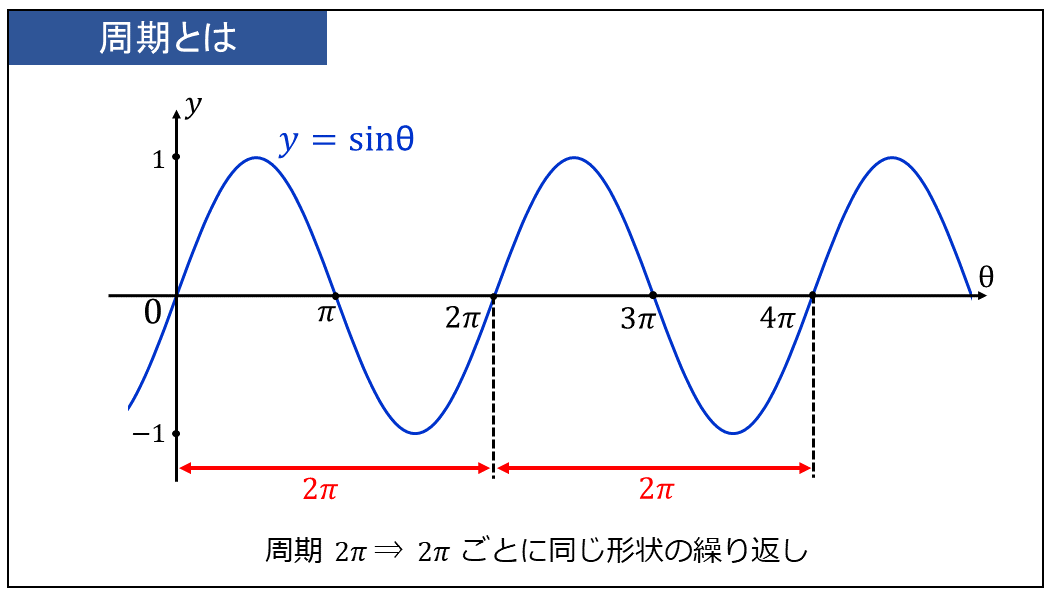
三角関数の性質から、\(\large{n}\)を整数とすると、\(\large{\sin \theta}\) には以下の式が成り立ちます。
$$\large{\sin (\theta + 2n \pi) = \sin \theta}$$
この式は、\(\large{y=\sin \theta}\) が \(\large{2\pi}\) の整数倍だけ平行移動しても、元の \(\large{y=\sin \theta}\) と一致することを意味します。
したがって、この三角関数の性質の式は \(\large{y=\sin \theta}\) の周期が \(\large{2 \pi}\) であることを表しています。
同様に、 $$\large{\cos (\theta + 2n \pi) = \cos \theta}$$ $$\large{\tan (\theta + 2n \pi) = \tan \theta}$$ の式は、\(\large{\cos\theta}\)、\(\large{\tan \theta}\) が \(\large{2 \pi}\) の周期をもつことを表しています。
ここで、三角関数の性質から、\(\large{\tan \theta}\) に関しては \(\large{\pi}\) だけ平行移動しても同じ式となります。 $$\large{\tan (\theta + \pi) = \tan \theta}$$ グラフの周期は、最も小さい正の数で表すため、『\(\large{\boldsymbol{y=\tan \theta}}\) の周期は \(\large{\boldsymbol{\pi}}\) 』となります。
・sin2θの周期
下図に \(\large{y=\sin \theta}\) と \(\large{y=\sin 2\theta}\) を比較したグラフを示します。
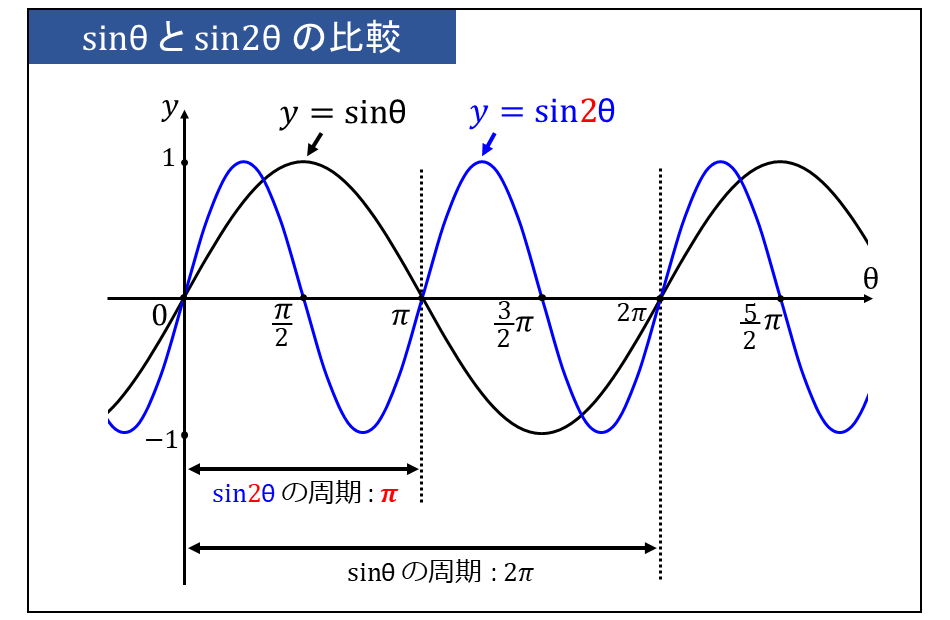
図に示すように、\(\large{y=\sin \theta}\) の周期が \(\large{2\pi}\) であるのに対し、 \(\large{y=\sin 2\theta}\) の周期は \(\large{\pi}\) となっています。
図からも分かるように、周期が \(\displaystyle \large{\frac{1}{2}}\)倍になると、グラフの横軸\(\large{\theta}\) に関して \(\displaystyle \large{\frac{1}{2}}\)倍 に縮小したグラフになる という関係があります。
一般的には、正の定数 \(\large{a}\) に対して以下が成り立ちます。
・\(\large{y=\tan a\theta}\) の周期は \(\displaystyle \large{\frac{\pi}{a}}\)
【2-3】三角関数の平行移動
下図に \(\large{y=\sin \theta}\) と \(\displaystyle \large{y=\sin (\theta-\frac{\pi}{2})}\) を比較したグラフを示します。
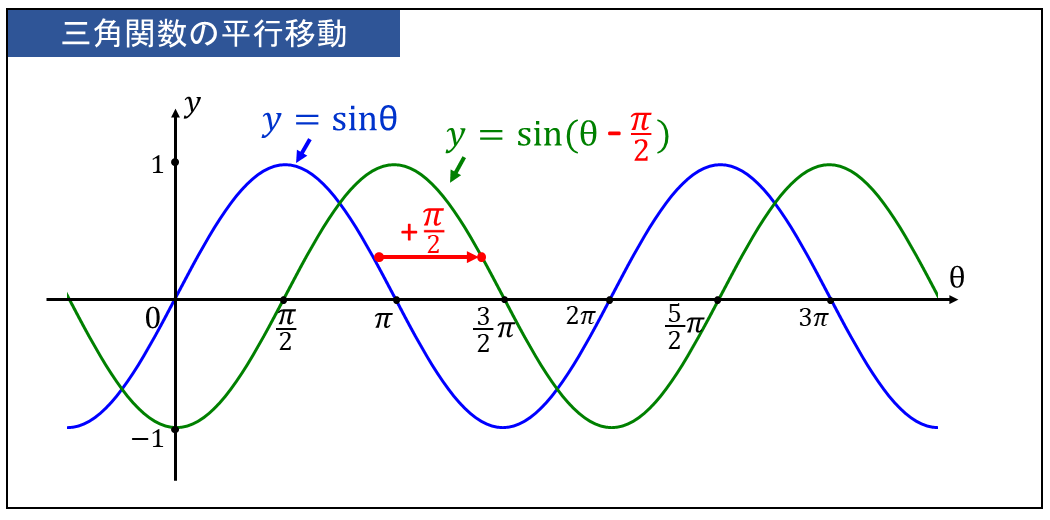
\(\large{y=\sin (\theta-\frac{\pi}{2})}\)のグラフは、\(\large{y=\sin \theta}\) を \(\large{\theta}\)軸の正方向に \(\displaystyle \large{+\frac{\pi}{2}}\) だけ平行移動したグラフとなります。
このとき、\(\large{\theta}\)方向へはグラフ全体が変化するため、周期には影響を与えません。
したがって、 \(\large{y=\sin \theta}\) と \(\displaystyle \large{y=\sin (\theta-\frac{\pi}{2})}\) のどちらも周期は \(\large{2 \pi}\) のままとなります。
・sinとcosのグラフの比較
下図に \(\large{y=\sin \theta}\) と \(\large{y=\cos \theta}\) を比較したグラフを示します。
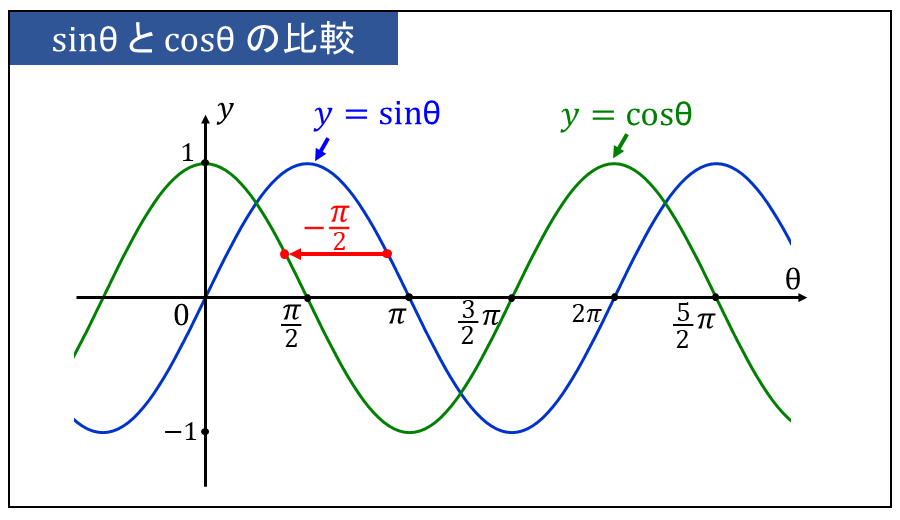
図に示されているように、\(\large{y=\sin \theta}\) を \(\large{\theta}\)軸の方向に \(\displaystyle \large{-\frac{\pi}{2}}\) だけ平行移動したグラフが \(\large{y=\cos \theta}\) と一致します。
この関係を数式で書き表すと、 $$\large{\displaystyle \sin\left(\theta + \frac{\pi}{2}\right) = \cos \theta}$$ となります。この関係式は三角関数の性質で導出方法を解説しています。
【3】グラフの書き方と周期の問題
本章では、以下の(1)~(3)の三角関数のグラフの書き方と周期を求める問題について解説します。
(1)sinのグラフの書き方 | 定数倍,平行移動
\(\displaystyle \large{y=2 \sin (\theta - \frac{\pi}{4})}\)
三角関数のグラフを書くときは、以下の手順で座標の位置を表にすると書きやすくなります。
以下の\(\large{a,b,c,d}\) が\(\large{1}\)でない場合に表の値を変換する
2. \(\large{y=a\sin \theta}\) (\(\large{y}\)軸方向に定数倍)
3. \(\large{y=a\sin b\theta}\) (\(\large{θ}\)軸方向に縮小/拡大)
4. \(\large{y=a\sin b(\theta-c)}\) (\(\large{θ}\)軸方向に平行移動)
5. \(\large{y=a\sin b(\theta-c)+d}\) (\(\large{y}\)軸方向に平行移動)
【解答と解説】
三角関数のグラフを書くときは、まず \(\large{y=\sin \theta}\) の座標を表にします。\(\displaystyle \large{\frac{\pi}{2}}\) 刻みで表を作ることで、グラフの概形を把握できます。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) | \(\displaystyle \large{2\pi}\) | \(\displaystyle \large{\frac{5}{2}\pi}\) | \(\displaystyle \large{3\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) |
次に、 \(\large{\sin \theta}\) を2倍した、 \(\large{y=2\sin \theta}\) の座標に変換します。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) | \(\displaystyle \large{2\pi}\) | \(\displaystyle \large{\frac{5}{2}\pi}\) | \(\displaystyle \large{3\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{-2}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{2}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-2}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{2}\) | \(\displaystyle \large{0}\) |
最後に、 \(\large{2\sin \theta}\) を平行移動した \(\large{y=2\sin (\theta-\frac{\pi}{4})}\) の座標に変換します。
(すべての \(\large{\theta}\) が \(\large{+\frac{\pi}{4}}\) だけ変化するように表を作ります。)
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{4}}\) | \(\displaystyle \large{\frac{\pi}{4}}\) | \(\displaystyle \large{\frac{3}{4}\pi}\) | \(\displaystyle \large{\frac{5}{4}\pi}\) | \(\displaystyle \large{\frac{7}{4}\pi}\) | \(\displaystyle \large{\frac{9}{4}\pi}\) | \(\displaystyle \large{\frac{11}{4}\pi}\) | \(\displaystyle \large{\frac{13}{4}\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{-2}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{2}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-2}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{2}\) | \(\displaystyle \large{0}\) |
以上の表から \(\large{y=2\sin (\theta-\frac{\pi}{4})}\) のグラフを書いた図を示します。
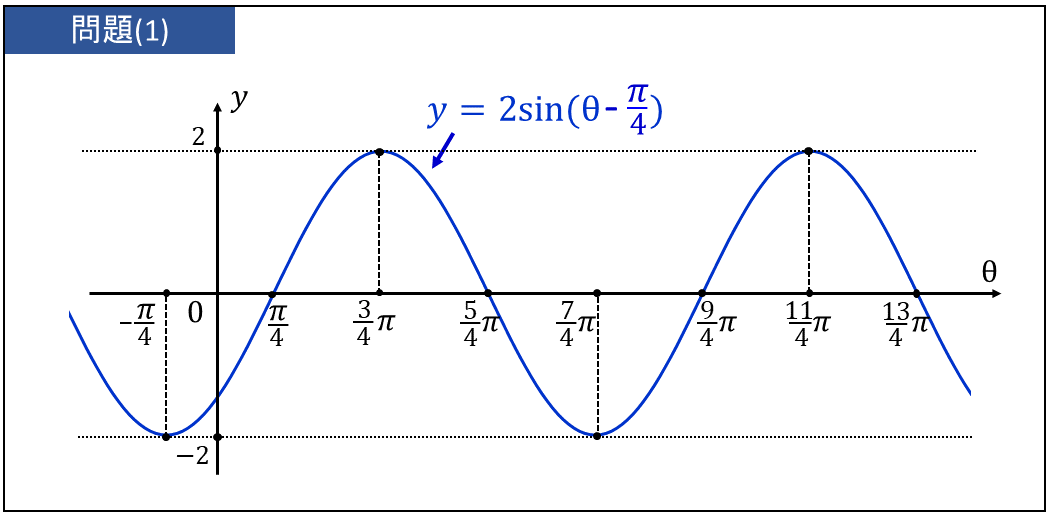
また、\(\large{y=2\sin (\theta-\frac{\pi}{4})}\) の周期は $$\large{\frac{2 \pi}{1} = 2\pi}$$ より、\(\large{2\pi}\) となります。
(2)cosのグラフの書き方 | 周期,平行移動
\(\displaystyle \large{y= \cos \frac{1}{2}\left(\theta - \frac{\pi}{2}\right)}\)
【解答と解説】
まず \(\large{y=\cos \theta}\) の座標を表にします。前問と同様に、\(\displaystyle \large{\frac{\pi}{2}}\) 刻みで表を作ります。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) | \(\displaystyle \large{2\pi}\) | \(\displaystyle \large{\frac{5}{2}\pi}\) | \(\displaystyle \large{3\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) |
ここで、\(\large{\cos \frac{1}{2}\theta}\) の周期は $$\large{2\pi \div \frac{1}{2} = 4\pi}$$ となるため、\(\large{\cos \frac{1}{2}\theta}\) は \(\large{\cos \theta}\) を\(\large{\theta}\)軸方向に2倍に引き延ばした形状となります。
よって、\(\large{y=\cos \theta}\) の座標を \(\large{y=\cos \frac{1}{2}\theta}\) の座標に変換すると、以下のようになります。
(\(\large{\theta}\)をすべて\(\large{2}\)倍した値に変換します。)
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\pi}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{2\pi}\) | \(\displaystyle \large{3\pi}\) | \(\displaystyle \large{4\pi}\) | \(\displaystyle \large{5\pi}\) | \(\displaystyle \large{6\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) |
最後に、\(\large{y=\cos \frac{1}{2}\theta}\) を平行移動した \(\large{y= \cos \frac{1}{2}\left(\theta - \frac{\pi}{2}\right)}\) の座標に変換します。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) | \(\displaystyle \large{\frac{5}{2}\pi}\) | \(\displaystyle \large{\frac{7}{2}\pi}\) | \(\displaystyle \large{\frac{9}{2}\pi}\) | \(\displaystyle \large{\frac{11}{2}\pi}\) | \(\displaystyle \large{\frac{13}{2}\pi}\) |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{-1}\) |
以上の表から \(\large{y= \cos \frac{1}{2}\left(\theta - \frac{\pi}{2}\right)}\) のグラフを書いた図を示します。
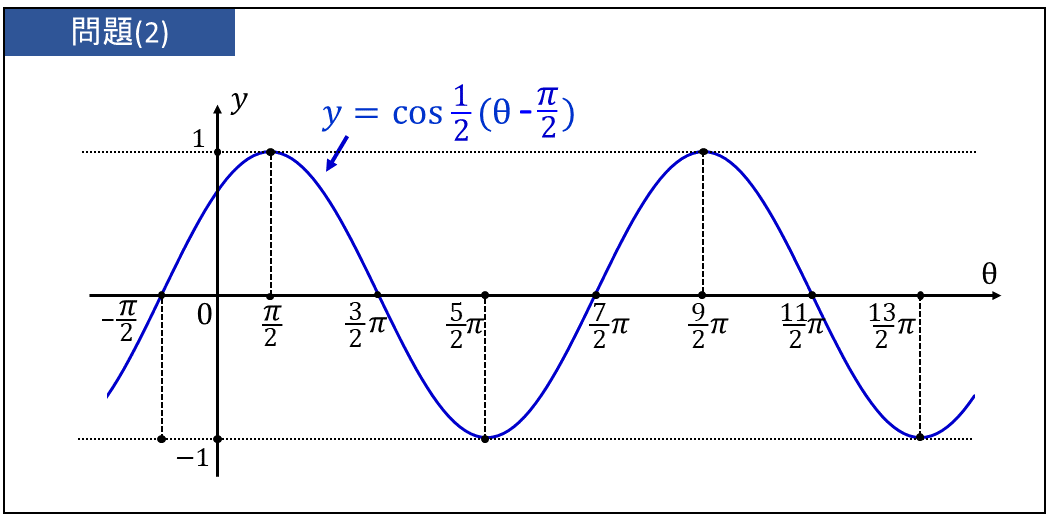
また、先述したように \(\large{y= \cos \frac{1}{2}\left(\theta - \frac{\pi}{2}\right)}\) の周期は $$\large{2 \pi \div \frac{1}{2} =4\pi}$$ より、\(\large{4\pi}\) となります。
(3)tanθのグラフ | 周期,平行移動
\(\displaystyle \large{y= \tan 2\theta+3}\)
【解答と解説】
まず \(\large{y=\tan \theta}\) の座標を表にします。\(\large{\tan}\) の場合は、\(\displaystyle \large{\frac{\pi}{2}}\) で発散してしまうため、\(\displaystyle \large{\tan \frac{\pi}{4} =1}\) を表に加えると書きやすくなります。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{2}}\) | \(\displaystyle \large{-\frac{\pi}{4}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{4}}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\frac{3}{4}\pi}\) | \(\displaystyle \large{\pi}\) | \(\displaystyle \large{\frac{5}{4}\pi}\) | \(\displaystyle \large{\frac{3}{2}\pi}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | - | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | - | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | - |
ここで、\(\large{\tan 2\theta}\) の周期は $$\large{\pi \div 2 = \frac{\pi}{2}}$$ となるため、\(\large{y=\tan 2\theta}\) のグラフは \(\large{y=\tan \theta}\) を \(\large{\theta}\)軸方向に\(\displaystyle \large{\frac{1}{2}}\)倍に縮小した形状となります。
よって、\(\large{y=\tan \theta}\) の座標を \(\large{y=\tan 2\theta}\) の座標に変換すると、以下のようになります。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{4}}\) | \(\displaystyle \large{-\frac{\pi}{8}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{8}}\) | \(\displaystyle \large{\frac{\pi}{4}}\) | \(\displaystyle \large{\frac{3}{8}\pi}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\frac{5}{8}\pi}\) | \(\displaystyle \large{\frac{3}{4}\pi}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | - | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | - | \(\displaystyle \large{-1}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{1}\) | - |
最後に、\(\large{y=\tan 2\theta}\) を \(\large{y}\)軸方向に平行移動した \(\large{y= \tan 2\theta + 3}\) の座標に変換します。
| \(\large{\boldsymbol{\theta}}\) | \(\displaystyle \large{-\frac{\pi}{4}}\) | \(\displaystyle \large{-\frac{\pi}{8}}\) | \(\displaystyle \large{0}\) | \(\displaystyle \large{\frac{\pi}{8}}\) | \(\displaystyle \large{\frac{\pi}{4}}\) | \(\displaystyle \large{\frac{3}{8}\pi}\) | \(\displaystyle \large{\frac{\pi}{2}}\) | \(\displaystyle \large{\frac{5}{8}\pi}\) | \(\displaystyle \large{\frac{3}{4}\pi}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \large{\boldsymbol{y}}\) | - | \(\displaystyle \large{2}\) | \(\displaystyle \large{3}\) | \(\displaystyle \large{4}\) | - | \(\displaystyle \large{2}\) | \(\displaystyle \large{3}\) | \(\displaystyle \large{4}\) | - |
以上の表から \(\large{y= \tan 2\theta+3}\) のグラフを書いた図を示します。
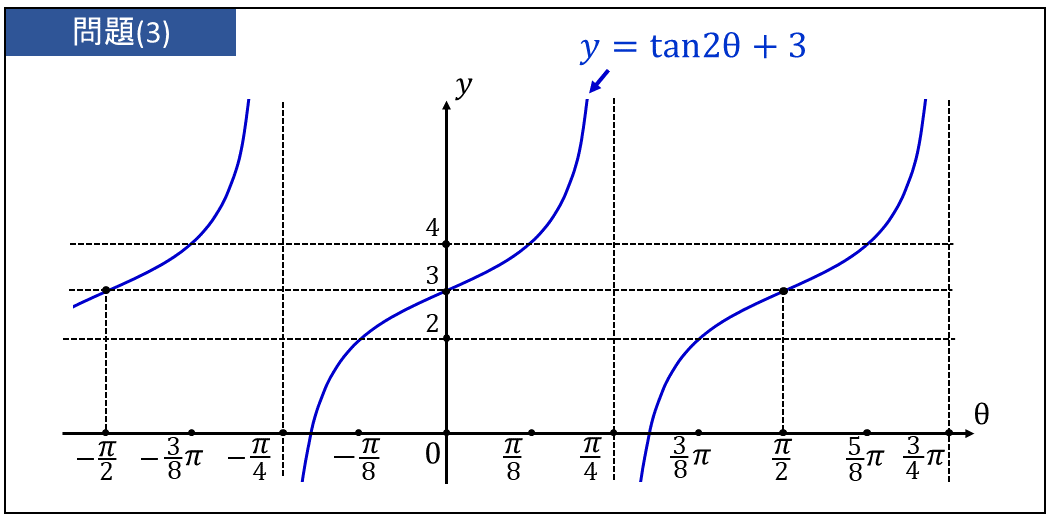
また、先述したように \(\large{y= \tan 2\theta+3}\) の周期は $$\displaystyle \large{ \pi \div 2 =\frac{\pi}{2}}$$ より、\(\displaystyle \large{\frac{\pi}{2}}\) となります。