-光と光学に関連する用語の解説サイト-

微分の英語表現と読み方

本項では以下の内容を解説しています。

・導関数や関数の傾きの英語表現
・微分の記号の読み方
・関連用語の一覧

1. 微分の英語表現
2. 微分記号の英語での読み方
3. 微分の英語用語のまとめ

【1】微分の英語表現

微分積分学を英語でcalculusといいます。特に、微分学という場合はdifferential calculusといいます。

【1-1】微分の英語表現

従属変数が$\large{y}$、独立変数が$\large{x}$であるような関数$\large{y=f(x)}$の場合、『xに関するyの微分』は英語で以下のように言い表します。

【xに関するyの微分】

derivative of y (with respect to x)

"with respect to x"と付けることで『$\large{x}$に関する』と説明することができます。

また、『xに関するyの二階微分』のように何階微分かを説明するときは、序数を使用して表現します。
例えば、『xに関するyの二階微分』は、second derivative of y with respect to xと言います。

yのn階微分を英語では"n-th derivative of y with respect to x"と表します。

意味	英語
一階微分	・(first) derivative of $\large{y}$ (with respect to x)
二階微分	・second derivative of $\large{y}$ (with respect to x)
三階微分	・third derivative of $\large{y}$ (with respect to x)
:	:
n階微分	・n-th derivative of $\large{y}$ (with respect to x)

【1-2】導関数の英語表現

従属変数が$\large{y}$、独立変数が$\large{x}$であるような関数$\large{y=f(x)}$の導関数は、以下の式により求められます。

【導関数/derivative function】

$$\large{ \displaystyle f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} }$$

導関数は、英語でderivative functionといいます。

導関数を定義する式を英語で表すと、"f prime of x is equal to the limit as h approaches 0 of f of x plus h minus f of x divided dy h."となります。

上記の英文の赤字は、数学の極限をとる操作を英語で表した部分です。例えば、$\large{\lim_{x \to a}}$を英語で表すと、"(the limit as) x approaches a"といいます。

もしくは、"(the limit as) x tends to a"、"(the limit as) x goes to a"などともいいます。

式	英語
$\large{x \rightarrow a }$ $\large{\lim_{x \to a}}$	・(the limit as) x approaches a ・(the limit as) x tends to a ・(the limit as) x goes to a

導関数は、微小変化量を表すギリシャ文字$\large{\Delta}$(デルタ)を使用して、$\large{ \displaystyle f'(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} }$とも表されます。
$\large{\Delta}$を使用した式を英語で言い表すと、"f prime of x is equal to the limit as delta x approaches 0 of delta y over delta x"となります。

("a over b"は分数$\Large{\frac{a}{b}}$を表す表現です。分数の英語表現は別ページに解説しています。)

【1-3】接線の傾き

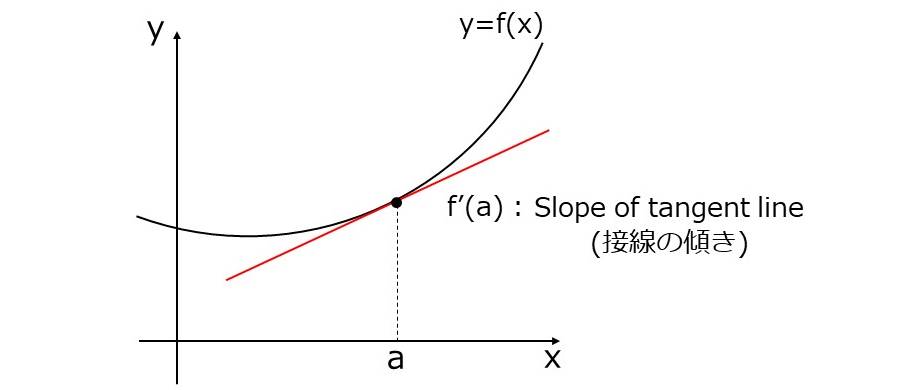
関数$\large{f(x)}$の導関数$\large{f'(x)}$接線の傾きを表しています。下図のように、$\large{f'(a)}$は$\large{x=a}$における接線の傾きとなります。微分の英語表現

グラフの接線は英語でtangent lineといいます。

ここで、『関数$\large{f(x)}$の$\large{x=a}$における傾きは$\large{f'(a)}$です。』を英語で表すと、"The slope of tangent line to $\large{f(x)}$ at $\large{\boldsymbol {x=a}}$ is $\large{f'(a)}$"となります。

【2】微分記号の英語での読み方

本章では、微分記号の英語での読み方について解説します。

微分の記法には、ライプニッツの記法やラグランジュの記法、ニュートンの記法などがあります。
本章では、この3つの記法について英語の表現を解説しています。

名称	微分記号の例
ライプニッツの記法	$\large{\displaystyle \frac{dy}{dx},\frac{d^2 y}{dx^2}}$
ラグランジュの記法	$\large{f'(x),f''(x)}$
ニュートンの記法	$\large{\dot{y},\ddot{y}}$

【2-1】ライプニッツの記法の英語の読み方

従属変数が$\large{y}$、独立変数が$\large{x}$であるような関数$\large{y=f(x)}$の導関数は、ライプニッツの記法では$\Large{\frac{dy}{dx}}$と記述されます。

$\Large{\frac{dy}{dx}}$は、"dy dx (ディーワイディーエックス)"と読みます。もしくは、"dy over dx"や"dy by dx"などと表す場合もあります。

また、二回微分は$\Large{\frac{d^2 y}{dx^2}}$のように記述されます。英語で読むと"d two y (over) dx two"と読みます。

もしくは、d squared y (over) dx squared などと読むこともあります。
(X squaredは『Xの2乗』を表す用語です。詳しくはべき乗の記事に記載しています。)

数式	意味	英語の読み方
$\large{ \displaystyle \frac{dy}{dx}}$	一階微分	・dy dx ・dy over dx ・dy by dx
$\large{ \displaystyle \frac{d^2y}{dx^2}}$	二階微分	・d two y (over) dx two ・d squared y (over) dx squared
$\large{\displaystyle \frac{d^3y}{dx^3}}$	三階微分	・d three y (over) dx three ・d cubed y (over) dx cubed
…	…	…
$\large{\displaystyle \frac{d^ny}{dx^n}}$	n階微分	・d n y (over) dx n

overは分数を表すときに使用されますが、微分記号を言い表すときは省略されることが多いです。 (分数の英語表現は別ページに解説しています。)

【2-2】ラグランジュの記法の英語の読み方

ラグランジュの記法では、関数$\large{f(x)}$の導関数は$\large{f'(x)}$と表記されます。
$\large{f'(x)}$は英語では、"f prime with respect to x"もしくは、"f prime of x"となります。

また、関数$\large{f(x)}$の二階微分は、$\large{f''(x)}$と表記され、英語では"f double prime with respect to x"となります。

数式	意味	英語の読み方
$\large{f'(x)}$	一階微分	・f prime of x
$\large{f''(x)}$	二階微分	・f double prime of x
$\large{f'''(x)}$	三階微分	・f triple prime of x

【1-3】ニュートンの記法の英語の読み方

ニュートンの記法では、従属変数の上部にドット記号『・』を使用することで微分を表します。
例えば、従属変数が$\large{y}$、独立変数が$\large{x}$であるような関数$\large{y=f(x)}$の導関数は、$\large{\dot{y}}$と書き表します。

$\large{\dot{y}}$を英語で表すと、"y dot"と読みます。また、二回微分を表す$\large{\ddot{y}}$は、"y double dot"と読みます。

数式	日本語	英語
$\large{\dot{y}}$	一階微分	・y dot
$\large{\ddot{y}}$	二階微分	・y double dot
$\large{\dddot{y}}$	三階微分	・y triple dot

【3】微分の英語用語のまとめ

本項で解説した微分に関連する英語表現の用語の一覧を示します。

用語	意味
calculus	・微分積分学
differential calculus	・微分学
derivative function	・導関数
slope	・傾き
tangent line	・接線
rate of change	・変化率
limit	・極限
first derivative of y	・yの一階微分
second derivative of y	・yの二階微分
third derivative of y	・yの三階微分
derivative of y with respect to x	・xに関するyの微分
higher-order derivative	・高階導関数

その他、微分に関連する英語表現の用語の一覧を示します。

用語	意味
inflection point	・変曲点
local minimum	・極小値
minimum	・最小値
local maximum	・極大値
maximum	・最大値
convex	・(関数の)凸面
concave	・(関数の)凹面

意味	英語
一階微分	・(first) derivative of \(\large{y}\) (with respect to x)
二階微分	・second derivative of \(\large{y}\) (with respect to x)
三階微分	・third derivative of \(\large{y}\) (with respect to x)
:	:
n階微分	・n-th derivative of \(\large{y}\) (with respect to x)

名称	微分記号の例
ライプニッツの記法	\(\large{\displaystyle \frac{dy}{dx},\frac{d^2 y}{dx^2}}\)
ラグランジュの記法	\(\large{f'(x),f''(x)}\)
ニュートンの記法	\(\large{\dot{y},\ddot{y}}\)

数式	意味	英語の読み方
\(\large{ \displaystyle \frac{dy}{dx}}\)	一階微分	・dy dx ・dy over dx ・dy by dx
\(\large{ \displaystyle \frac{d^2y}{dx^2}}\)	二階微分	・d two y (over) dx two ・d squared y (over) dx squared
\(\large{\displaystyle \frac{d^3y}{dx^3}}\)	三階微分	・d three y (over) dx three ・d cubed y (over) dx cubed
…	…	…
\(\large{\displaystyle \frac{d^ny}{dx^n}}\)	n階微分	・d n y (over) dx n

数式	意味	英語の読み方
\(\large{f'(x)}\)	一階微分	・f prime of x
\(\large{f''(x)}\)	二階微分	・f double prime of x
\(\large{f'''(x)}\)	三階微分	・f triple prime of x

数式	日本語	英語
\(\large{\dot{y}}\)	一階微分	・y dot
\(\large{\ddot{y}}\)	二階微分	・y double dot
\(\large{\dddot{y}}\)	三階微分	・y triple dot