同じものを含む順列 | 問題と解き方
本項では以下の内容を解説しています。
- ・同じものを含む順列とは
- ・同じものを含む順列の公式
- ・問題の一覧
【1】同じものを含む順列とは
"同じものを含む順列"とは、複数のものから同じ種類を含むものを選び並べる順列のことです。
同じものを含む順列の例として \(\large{\rm{\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt}}}\) の\(\large{\hspace{1pt}6\hspace{1pt}}\)つの文字を並べる並べ方の数を求める問題について考えます。
・例題
まず、すべての文字が区別できるものとして \(\large{\rm{\hspace{1pt}A_1\hspace{2pt},\hspace{1pt}A_2\hspace{2pt},\hspace{1pt}A_3\hspace{2pt},\hspace{1pt}B_1\hspace{2pt},\hspace{1pt}B_2\hspace{2pt},\hspace{1pt}C\hspace{1pt}}}\) と名前を付けて並べ方の総数を求めると、順列の公式から $$\large{{}_6 P_{\hspace{1pt}6} = 6 \hspace{1pt}!}$$ と求められます。
ここで、\(\large{\rm{\hspace{1pt}A_1\hspace{1pt},\hspace{1pt}A_2\hspace{1pt},\hspace{1pt}A_3\hspace{1pt}}}\) は元は区別できない\(\large{\rm{\hspace{1pt}A\hspace{2pt}}}\)であり、\(\large{\hspace{1pt}3\hspace{1pt}}\)つを入れ替えた\(\large{\hspace{1pt}3\hspace{1pt}!\hspace{1pt}}\)通りの分だけ多く並べ方を求めています。
また、\(\large{\rm{\hspace{1pt}B_1\hspace{1pt},\hspace{1pt}B_2\hspace{1pt}}}\) も元は区別できない\(\large{\rm{\hspace{1pt}B\hspace{2pt}}}\)であるため、\(\large{\hspace{1pt}2\hspace{1pt}}\)つを入れ替えた\(\large{\hspace{1pt}2\hspace{1pt}!\hspace{1pt}}\)通りの分だけ多く並べ方を求めています。
つまり、\(\large{\rm{\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt}}}\) の\(\large{\hspace{1pt}6\hspace{1pt}}\)つの文字を一列に並べる並べ方は \begin{eqnarray} \large \frac{6\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{3\cdot 2 \cdot 1 \cdot 2 \cdot 1 \cdot 1} \\[0.7em] \large & \large = & \large 60\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}60\hspace{1pt}}\)通りとなります。
・例題の別解
例題の別解として、\(\large{\rm{\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt}}}\) の\(\large{\hspace{1pt}6\hspace{1pt}}\)つの文字を並べる場所を選ぶという考え方で解くこともできます。
\(\large{\rm{\hspace{1pt}A\hspace{1pt}}}\)の位置の決め方は\(\large{\hspace{1pt}6\hspace{1pt}}\)個の場所から、\(\large{\hspace{1pt}3\hspace{1pt}}\)個の場所を選ぶ方法であるため、\(\large{\hspace{1pt}{}_6 C_3\hspace{1pt}}\)通りあります。
そのおのおのに対して、\(\large{\rm{\hspace{1pt}B\hspace{1pt}}}\)の位置は残りの\(\large{\hspace{1pt}3\hspace{1pt}}\)個の場所から、\(\large{\hspace{1pt}2\hspace{1pt}}\)個の場所を選ぶため、\(\large{\hspace{1pt}{}_3 C_2\hspace{1pt}}\)通りあります。
\(\large{\rm{\hspace{1pt}C\hspace{1pt}}}\)の位置は残りの\(\large{\hspace{1pt}1\hspace{1pt}}\)個の場所におくと考えます。
つまり、\(\large{\rm{\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt}}}\) の\(\large{\hspace{1pt}6\hspace{1pt}}\)つの文字を一列に並べる並べ方は \begin{eqnarray} \large {}_6 C_3 \times {}_3 C_2 \times {}_1 C_1 & \large = & \large \frac{6\cdot 5 \cdot 4}{3\hspace{1pt}! } \times \frac{3\cdot 2 }{ 2\hspace{1pt}! } \times \frac{1 }{ 1\hspace{1pt}! }\\[0.7em] \large & \large = & \large \frac{6\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!}\\[0.7em] \large & \large = & \large 60\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}60\hspace{1pt}}\)通りとなります。
・同じものを含む順列の公式
一般的には、異なる\(\large{\hspace{1pt}n\hspace{2pt}}\)個のものから\(\large{\hspace{1pt}p\hspace{2pt}}\)個の同じもの、別の種類の\(\large{\hspace{1pt}q\hspace{2pt}}\)個の同じもの、別の種類の\(\large{\hspace{1pt}r\hspace{2pt}}\)個の同じもの\(\large{\hspace{1pt}\cdots\hspace{2pt}}\)を取り出して並べる並べ方の総数は以下の公式で表されます。
ただし、\(\large{\hspace{1pt}p+q+r+\cdots = n\hspace{1pt}}\)
【2】同じものを含む順列の問題
本章では、同じものを含む順列に関連する問題と解き方について解説します。
\(\large{(1)\hspace{5pt}}\)\(\large{\hspace{1pt}9\hspace{1pt}}\)文字の並べ方\(\large{\hspace{32pt}}\)
\(\large{(2)\hspace{5pt}}\)両端が\(\large{\hspace{1pt}\rm{C}\hspace{2pt}}\)となる並べ方
\(\large{(3)\hspace{5pt}}\)左右対称となる並べ方
解答と解説 : 問題1
\(\large{(1)\hspace{5pt}}\)\(\large{\hspace{1pt}10\hspace{1pt}}\)文字の並べ方\(\large{\hspace{52pt}}\)
\(\large{(2)\hspace{5pt}}\)\(\large{\hspace{1pt}\rm{I}\hspace{2pt}}\)が隣り合うときの並べ方\(\large{\hspace{9pt}}\)
\(\large{(3)\hspace{5pt}}\)\(\large{\hspace{1pt}\rm{A}\hspace{1pt},\hspace{1pt}\rm{C}\hspace{3pt}}\)がこの順となる並べ方
解答と解説 : 問題2
\(\large{(1)\hspace{5pt}}\)整数は何通りできるか
\(\large{(2)\hspace{5pt}}\)偶数は何通りできるか
\(\large{(3)\hspace{5pt}}\)奇数は何通りできるか
解答と解説 : 問題3
解答と解説 : 問題4
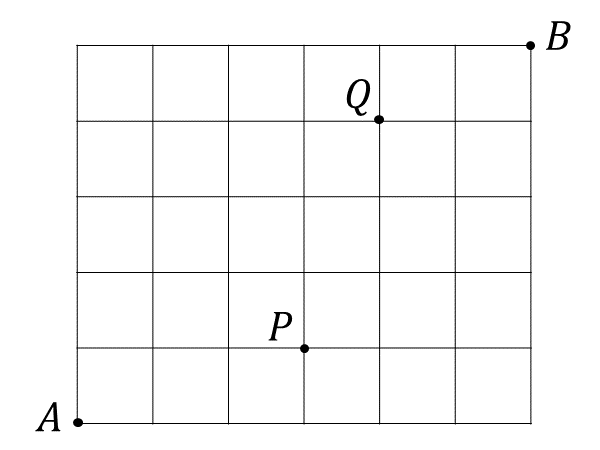
\(\large{(1)\hspace{5pt}}\)全ての経路\(\large{\hspace{50pt}}\)
\(\large{(2)\hspace{5pt}}\)点\(\large{\hspace{1pt}P\hspace{2pt}}\)を通る経路\(\large{\hspace{30pt}}\)
\(\large{(3)\hspace{5pt}}\)点\(\large{\hspace{1pt}P\hspace{2pt}}\)を通らない経路\(\large{\hspace{11pt}}\)
\(\large{(4)\hspace{5pt}}\)点\(\large{\hspace{1pt}P\hspace{2pt}}\)と点\(\large{\hspace{1pt}Q\hspace{2pt}}\)を通る経路
解答と解説 : 問題5
問題1の解答 : アルファベットの並べ方の問題
\(\large{(1)\hspace{5pt}}\)\(\large{\hspace{1pt}9\hspace{1pt}}\)文字の並べ方\(\large{\hspace{32pt}}\)
\(\large{(2)\hspace{5pt}}\)両端が\(\large{\hspace{1pt}\rm{C}\hspace{2pt}}\)となる並べ方
\(\large{(3)\hspace{5pt}}\)左右対称となる並べ方
問題(1)の解答 | 同じ文字を含む並べ方の問題
文字を一列に並べる方法は、同じものを含む順列の公式から \begin{eqnarray} \large \frac{9\hspace{1pt}!}{5\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!} & \large = & \large \frac{9 \cdot 8 \cdot 7 \cdot 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{120 \cdot 2 \cdot 2 } \\[0.7em] \large & \large = & \large 756\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}756\hspace{1pt}}\)通りとなります。
問題(2)の解答 | 両端を指定された並べ方の問題
まず、両端に\(\large{\hspace{1pt}\rm{C}\hspace{2pt}}\)を並べると考えます。どちらも\(\large{\hspace{1pt}\rm{C}\hspace{1pt}}\)であるため、並べ方は\(\large{\hspace{1pt}1\hspace{1pt}}\)通りとなります。
\(\large{\hspace{1pt}\rm{C}\hspace{2pt}}\)を並べた後、両端の間に\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)を\(\large{\hspace{1pt}5\hspace{1pt}}\)個並べる方法を求めればよいため、同じものを含む順列の公式から \begin{eqnarray} \large 1 \times \frac{7\hspace{1pt}!}{5\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!} & \large = & \large \frac{7\cdot 6 \cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{120 \cdot 2 } \\[0.7em] \large & \large = & \large 21\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}21\hspace{1pt}}\)通りとなります。
問題(3)の解答 | 左右対称となる並べ方の問題
まず、左右対称となるためには真ん中に\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)を並べる必要があります。
また、真ん中から左側の並び方を決めれば、右側の並び方も\(\large{\hspace{1pt}1\hspace{1pt}}\)通りに決まるため、\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)が\(\large{\hspace{1pt}1\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)が\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{C}\hspace{1pt}}\)が\(\large{\hspace{1pt}1\hspace{1pt}}\)個の順列を求めることで左右対称な場合の並べ方の数が求められます。
したがって、 \begin{eqnarray} \large \frac{4\hspace{1pt}!}{2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 4\cdot 3 \cdot 2 \cdot 1}{ 2 } \\[0.7em] \large & \large = & \large 12\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}12\hspace{1pt}}\)通りとなります。
問題2の解答 : 文字列の並び替えの問題
\(\large{(1)\hspace{5pt}}\)\(\large{\hspace{1pt}10\hspace{1pt}}\)文字の並べ方\(\large{\hspace{52pt}}\)
\(\large{(2)\hspace{5pt}}\)\(\large{\hspace{1pt}\rm{I}\hspace{2pt}}\)が隣り合うときの並べ方\(\large{\hspace{9pt}}\)
\(\large{(3)\hspace{5pt}}\)\(\large{\hspace{1pt}\rm{A}\hspace{1pt},\hspace{1pt}\rm{C}\hspace{3pt}}\)がこの順となる並べ方
問題(1)の解答 | 文字列の並び替えの問題
まず、文字の種類ごとに数えておきます。
\(\large{\hspace{1pt}\rm{S\hspace{1pt}T\hspace{1pt}A\hspace{1pt}T\hspace{1pt}I\hspace{1pt}S\hspace{1pt}T\hspace{1pt}I\hspace{1pt}C\hspace{1pt}S}\hspace{1pt}}\)には\(\large{\hspace{2pt}\rm{S}\hspace{1pt}}\)が\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{T}\hspace{1pt}}\)が\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{I}\hspace{1pt}}\)が\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{A}\hspace{1pt}}\)と\(\large{\hspace{1pt}\rm{C}\hspace{1pt}}\)が\(\large{\hspace{1pt}1\hspace{1pt}}\)個ずつあります。
これらの文字を一列に並べる方法は、同じものを含む順列の公式から \begin{eqnarray} \large \frac{10\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{10\cdot 9 \cdot 8\cdot 7 \cdot 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 \cdot 6 \cdot 2} \\[0.7em] \large & \large = & \large 50400\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}50400\hspace{1pt}}\)通りとなります。
問題(2)の解答 | 文字が隣り合う文字列の問題
隣り合う\(\large{\hspace{1pt}2\hspace{1pt}}\)個の\(\large{\hspace{1pt}\rm{I}\hspace{2pt}}\)をまとめて\(\large{\hspace{2pt}\rm{I\hspace{1pt}'}\hspace{2pt}}\)と考えて文字の並び方を考えます。
すなわち、\(\large{\hspace{2pt}\rm{S}\hspace{1pt}}\)が\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{T}\hspace{1pt}}\)が\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{I\hspace{1pt}'}\hspace{2pt}}\)と\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)と\(\large{\hspace{1pt}\rm{C}\hspace{2pt}}\)が\(\large{\hspace{1pt}1\hspace{1pt}}\)個の並び方を考えます。
これらの文字を一列に並べる方法は、同じものを含む順列の公式から \begin{eqnarray} \large \frac{9\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}3\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 9 \cdot 8\cdot 7 \cdot 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 \cdot 6 } \\[0.7em] \large & \large = & \large 10080\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}10080\hspace{1pt}}\)通りとなります。
問題(3)の解答 | 文字の並びを指定された文字列の問題
\(\large{\hspace{1pt}\rm{A}\hspace{1pt},\hspace{1pt}\rm{C}\hspace{3pt}}\)の並び方が指定されている場合、これらの文字を\(\large{\hspace{1pt}〇\hspace{2pt}}\)とおいて、文字を並べた後に\(\large{\hspace{1pt}\rm{A}\hspace{1pt},\hspace{1pt}\rm{C}\hspace{1pt}}\)の順に文字を入れると考えます。
すなわち、\(\large{\hspace{2pt}\rm{S}\hspace{2pt}}\)が\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{T}\hspace{2pt}}\)が\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}\rm{I}\hspace{2pt}}\)が\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}〇\hspace{1pt}}\)が\(\large{\hspace{1pt}2\hspace{1pt}}\)個の並び方を考えます。
このとき\(\large{\hspace{1pt}〇\hspace{2pt}}\)に\(\large{\hspace{1pt}\rm{A}\hspace{1pt},\hspace{1pt}\rm{C}\hspace{1pt}}\)の順に文字を入れる並べ方は\(\large{\hspace{1pt}1\hspace{1pt}}\)通りとなります。
つまり、同じものを含む順列の公式から \begin{eqnarray} \large \frac{10\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!} \times 1 & \large = & \large \frac{10\cdot 9 \cdot 8\cdot 7 \cdot 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 \cdot 6 \cdot 2 \cdot 2 } \\[0.7em] \large & \large = & \large 25200\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}25200\hspace{1pt}}\)通りとなります。
問題3の解答 : 数字を作る問題
\(\large{(1)\hspace{5pt}}\)整数は何通りできるか
\(\large{(2)\hspace{5pt}}\)偶数は何通りできるか
\(\large{(3)\hspace{5pt}}\)奇数は何通りできるか
問題(1)の解答 | 整数を作る
\(\large{\hspace{1pt}1\hspace{1pt}}\)を\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}2\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}3\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個を一列に並べる方法は、同じものを含む順列の公式から \begin{eqnarray} \large \frac{7\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!} & \large = & \large \frac{ 7 \cdot 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 \cdot 2 \cdot 2} \\[0.7em] \large & \large = & \large 210\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}210\hspace{1pt}}\)通りとなります。
問題(2)の解答 | 偶数を作る
数が偶数となるためには、一の位が\(\large{\hspace{1pt}2\hspace{1pt}}\)である必要があります。
残りの桁に\(\large{\hspace{1pt}1\hspace{1pt}}\)を\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}2\hspace{1pt}}\)を\(\large{\hspace{1pt}1\hspace{1pt}}\)個、\(\large{\hspace{1pt}3\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個並べる方法の数を求めれば、作られる偶数の数となります。
同じものを含む順列の公式から\begin{eqnarray} \large \frac{6\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 \cdot 2} \\[0.7em] \large & \large = & \large 60\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}60\hspace{1pt}}\)通りとなります。
問題(3)の解答 | 奇数を作る
数が奇数となるためには、一の位が\(\large{\hspace{1pt}1\hspace{1pt}}\)または\(\large{\hspace{1pt}3\hspace{1pt}}\)である必要があります。
ここで、一の位が\(\large{\hspace{1pt}1\hspace{2pt}}\)か\(\large{\hspace{1pt}3\hspace{2pt}}\)かで残りの桁に使用する数字が変化するため、場合分けが必要になります。
・一の位が\(\large{\hspace{1pt}1\hspace{1pt}}\)のとき
残りの桁に\(\large{\hspace{1pt}1\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}2\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}3\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個並べる方法の数を求めます。
同じものを含む順列の公式から\begin{eqnarray} \large \frac{6\hspace{1pt}!}{2\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!} & \large = & \large \frac{ 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{2 \cdot 2 \cdot 2} \\[0.7em] \large & \large = & \large 90\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}90\hspace{1pt}}\)通りとなります。
・一の位が\(\large{\hspace{1pt}3\hspace{1pt}}\)のとき
残りの桁に\(\large{\hspace{1pt}1\hspace{1pt}}\)を\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}2\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}3\hspace{1pt}}\)を\(\large{\hspace{1pt}1\hspace{1pt}}\)個並べる方法の数を求めます。
同じものを含む順列の公式から\begin{eqnarray} \large \frac{6\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 6\cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 \cdot 2 } \\[0.7em] \large & \large = & \large 60\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}60\hspace{1pt}}\)通りとなります。
以上から、一の位が\(\large{\hspace{1pt}1\hspace{1pt}}\)のときと\(\large{\hspace{1pt}3\hspace{1pt}}\)のときにできる数字の数を足すことで、奇数となる数を求めると $$\large{90+60 =150}$$ したがって、\(\large{\hspace{1pt}150\hspace{1pt}}\)通りとなります。
問題4の解答 : 0を含む数を並べる問題
問題の解答 | 0を含む数から整数を作る
本問では、選択する数字に\(\large{\hspace{1pt}0\hspace{1pt}}\)が含まれているため、まず十万の位に\(\large{\hspace{1pt}0\hspace{2pt}}\)以外の数字を選びます。
十万の位には、\(\large{\hspace{1pt}1\hspace{2pt}}\)または\(\large{\hspace{1pt}2\hspace{2pt}}\)の\(\large{\hspace{1pt}2\hspace{1pt}}\)通りの数字が入ります。
前問と同様に、十万の位が\(\large{\hspace{1pt}1\hspace{1pt}}\)か\(\large{\hspace{1pt}2\hspace{2pt}}\)かで残りの桁に使用する数字が変化するため、場合分けが必要になります。
・十万の位が\(\large{\hspace{1pt}1\hspace{1pt}}\)のとき
残りの桁に\(\large{\hspace{1pt}0\hspace{1pt}}\)を\(\large{\hspace{1pt}1\hspace{1pt}}\)個、\(\large{\hspace{1pt}1\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個、\(\large{\hspace{1pt}2\hspace{1pt}}\)を\(\large{\hspace{1pt}2\hspace{1pt}}\)個並べる方法の数を求めれば、作られる整数の数となります。
同じものを含む順列の公式から\begin{eqnarray} \large \frac{5\hspace{1pt}!}{2\hspace{1pt}!\hspace{1pt}2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{ 2 \cdot 2} \\[0.7em] \large & \large = & \large 30\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}30\hspace{1pt}}\)通りとなります。
・十万の位が\(\large{\hspace{1pt}2\hspace{1pt}}\)のとき
残りの桁に\(\large{\hspace{1pt}0\hspace{1pt}}\)を\(\large{\hspace{1pt}1\hspace{1pt}}\)個、\(\large{\hspace{1pt}1\hspace{1pt}}\)を\(\large{\hspace{1pt}3\hspace{1pt}}\)個、\(\large{\hspace{1pt}2\hspace{1pt}}\)を\(\large{\hspace{1pt}1\hspace{1pt}}\)個並べる方法の数を求めれば、作られる整数の数となります。
同じものを含む順列の公式から\begin{eqnarray} \large \frac{5\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 } \\[0.7em] \large & \large = & \large 20\\[0.7em] \end{eqnarray}
したがって、\(\large{\hspace{1pt}20\hspace{2pt}}\)通りとなります。
以上から、十万の位が\(\large{\hspace{1pt}1\hspace{2pt}}\)のときと\(\large{\hspace{1pt}2\hspace{2pt}}\)のときにできる整数の数を足すと $$\large{30+20 =50}$$ となります。
したがって、整数の数は\(\large{\hspace{1pt}50\hspace{2pt}}\)通りとなります。
問題5の解答 : 最短経路を求める問題

\(\large{(1)\hspace{5pt}}\)全ての経路\(\large{\hspace{50pt}}\)
\(\large{(2)\hspace{5pt}}\)点\(\large{\hspace{1pt}P\hspace{2pt}}\)を通る経路\(\large{\hspace{30pt}}\)
\(\large{(3)\hspace{5pt}}\)点\(\large{\hspace{1pt}P\hspace{2pt}}\)を通らない経路\(\large{\hspace{11pt}}\)
\(\large{(4)\hspace{5pt}}\)点\(\large{\hspace{1pt}P\hspace{2pt}}\)と点\(\large{\hspace{1pt}Q\hspace{2pt}}\)を通る経路
問題(1)の解答 | 最短経路の問題
本問は右へ行くことを『→』、上へ行くことを 『↑』とすれば『→』と『↑』の記号を並べる順列と考えることができます。
問題(1)は、点\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)まで移動するためには右へ\(\large{\hspace{1pt}6\hspace{1pt}}\)回、上へ\(\large{\hspace{1pt}5\hspace{1pt}}\)回移動すればよいので、『→』を\(\large{\hspace{1pt}6\hspace{1pt}}\)個と『↑』を\(\large{\hspace{1pt}5\hspace{1pt}}\)個並べる順列を計算します。
同じものを含む順列の公式から \begin{eqnarray} \large \frac{11\hspace{1pt}!}{6\hspace{1pt}!\hspace{1pt}5\hspace{1pt}!} & \large = & \large \frac{ 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{6 } \\[0.7em] \large & \large = & \large 462\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}462\hspace{1pt}}\)通りとなります。
問題(2)の解答 | 点Pを通る最短経路の問題
問題(2)は、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)を通る経路を求めるため、点\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)まで行く経路と、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)まで行く経路をそれぞれ計算してかけ合わせます。
点\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)まで行く経路の数は \begin{eqnarray} \large \frac{4\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 4\cdot 3 \cdot 2 \cdot 1}{6 } \\[0.7em] \large & \large = & \large 4\\[0.7em] \end{eqnarray} つまり、\(\large{\hspace{1pt}4\hspace{1pt}}\)通りとなります。
また、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)まで行く経路の数は \begin{eqnarray} \large \frac{7\hspace{1pt}!}{4\hspace{1pt}!\hspace{1pt}3\hspace{1pt}!} & \large = & \large \frac{ 7\cdot 6 \cdot 5 \cdot 4\cdot 3 \cdot 2 \cdot 1}{24 \cdot 6 } \\[0.7em] \large & \large = & \large 35\\[0.7em] \end{eqnarray} つまり\(\large{\hspace{1pt}35\hspace{1pt}}\)通りとなります。
したがって、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)を通る最短経路は $$\large{4 \times 35 =140}$$ から\(\large{\hspace{1pt}140\hspace{1pt}}\)通りとなります。
問題(3)の解答 | 点Pを通らない最短経路の問題
点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)を通らない経路を求めるには、(全ての経路)-(点\(\large{\hspace{1pt}\rm{P}\hspace{1pt}}\)を通る経路) を計算することで求めます。
したがって、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)を通らない最短経路は $$\large{462 - 140 = 322}$$ から\(\large{\hspace{1pt}322\hspace{1pt}}\)通りとなります。
問題(4)の解答 | 点Pと点Qを通る最短経路の問題
問題(4)は、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)と点\(\large{\hspace{1pt}\rm{Q}\hspace{2pt}}\)を通る経路を求めるため、点\(\large{\hspace{1pt}A\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{Q}\hspace{2pt}}\)、点\(\large{\hspace{1pt}\rm{Q}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)まで行く経路をそれぞれ計算してかけ合わせます。
点\(\large{\hspace{1pt}\rm{A}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)まで行く経路の数は \begin{eqnarray} \large \frac{4\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 4\cdot 3 \cdot 2 \cdot 1}{6 } \\[0.7em] \large & \large = & \large 4\\[0.7em] \end{eqnarray} つまり、\(\large{\hspace{1pt}4\hspace{1pt}}\)通りとなります。
また、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{Q}\hspace{2pt}}\)まで行く経路の数は \begin{eqnarray} \large \frac{4\hspace{1pt}!}{3\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 4\cdot 3 \cdot 2 \cdot 1}{ 6 } \\[0.7em] \large & \large = & \large 4\\[0.7em] \end{eqnarray} つまり\(\large{\hspace{1pt}4\hspace{1pt}}\)通りとなります。
また、点\(\large{\hspace{1pt}\rm{Q}\hspace{2pt}}\)から点\(\large{\hspace{1pt}\rm{B}\hspace{2pt}}\)まで行く経路の数は \begin{eqnarray} \large \frac{3\hspace{1pt}!}{2\hspace{1pt}!\hspace{1pt}1\hspace{1pt}!} & \large = & \large \frac{ 3 \cdot 2 \cdot 1}{ 2 } \\[0.7em] \large & \large = & \large 3\\[0.7em] \end{eqnarray} つまり\(\large{\hspace{1pt}3\hspace{1pt}}\)通りとなります。
したがって、点\(\large{\hspace{1pt}\rm{P}\hspace{2pt}}\)と点\(\large{\hspace{1pt}\rm{Q}\hspace{2pt}}\)を通る最短経路は $$\large{4 \times 4 \times 3 =48}$$ から\(\large{\hspace{1pt}48\hspace{1pt}}\)通りとなります。