順列の公式と問題の一覧

本項では以下の内容を解説しています。

• ・順列とは
• ・順列の公式
• ・問題の一覧

【1】順列とは

順列とは、異なる複数のものから、順序を考えて並べたものを意味します。

例えば、\(\large{A\hspace{1pt},\hspace{2pt}B\hspace{1pt},\hspace{2pt}C\hspace{1pt}}\) の \(\large{3\hspace{1pt}}\)つの文字を並べた順列の数について考えます。

まず、文字の並べ方のパターンを樹形図を用いて書き出してみます。

左側に最初の文字、真ん中に\(\large{\hspace{1pt}2\hspace{2pt}}\)番目の文字、右側に\(\large{\hspace{1pt}3\hspace{2pt}}\)番目の文字を配置して樹形図を作ると、以下のようになります。

\(\large{3\hspace{1pt}}\)つの文字を並べたとき、最初の文字は \(\large{\color{#e00d0d}{3}\hspace{1pt}}\)種類 から選ばれます。
次は、\(\large{3\hspace{1pt}}\)つの文字から最初の文字を除いた \(\large{\color{#e00d0d}{2}\hspace{1pt}}\)種類 から選びます。
最後に、残りの \(\large{\color{#e00d0d}{1}\hspace{1pt}}\)種類 を並べます。

樹形図から、\(\large{3\hspace{1pt}}\)つの文字を並べた順列は \(\large{6\hspace{1pt}}\)通り と求めることができます。

計算から求める場合、\(\large{3\hspace{1pt}}\)つの文字の並べ方は $$\large{3 \times 2 \times 1 = 6}$$ から \(\large{6\hspace{1pt}}\)通り と求めることができます。

・階乗の計算

先述のように、\(\large{3\hspace{1pt}}\)つの文字の並べ方は $$\large{3 \times 2 \times 1 = 6}$$ から計算されます。

\(\large{3 \times 2 \times 1}\) のように ある自然数から \(\large{1\hspace{1pt}}\)づつ数字を減らして掛け合わせる計算を階乗といい $$\large{3\hspace{1pt}! = 3 \times 2 \times 1}$$ と表します。

ここで、\(\large{\hspace{2pt}n\hspace{1pt}}\)個のものから全てを使ったときの並べ方の総数は、階乗の計算から以下のように求められます。

・例題

\(\large{\hspace{2pt}5\hspace{1pt}}\)個の文字から全てを使ったときの並べ方は \(\large{5\hspace{1pt}!}\) 通りと求められます。

したがって、 \begin{eqnarray} \large 5\hspace{1pt}! & \large = & \large 5\times 4 \times 3 \times 2 \times 1 \\[0.7em] \large & \large = & \large 120 \\[0.7em] \end{eqnarray}

以上から、\(\large{\hspace{2pt}5\hspace{1pt}}\)個の文字の並べ方は \(\large{120\hspace{1pt}}\)通りとなります。

【2】順列の公式

次に、異なる複数のものから 一部を選び並べる問題について考えます。

以下のような \(\large{3\hspace{1pt}}\)つの空欄に\(\large{1\hspace{1pt}}\)つずつ文字を当てはめると考えます。

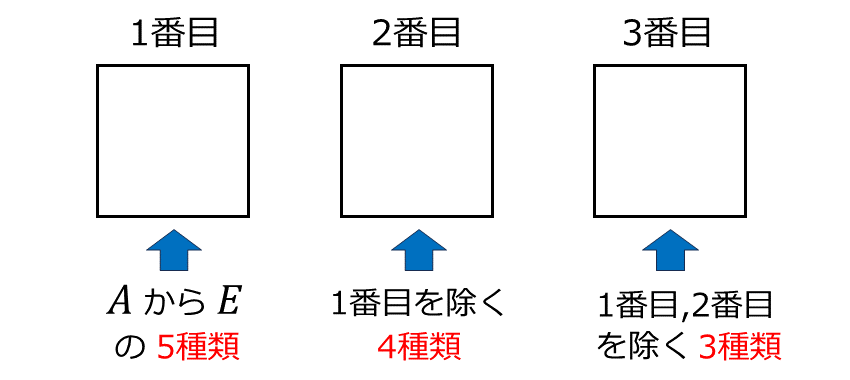
左側の空欄は \(\large{\color{#e00d0d}{5}\hspace{1pt}}\)種類 の文字から選びます。
真ん中の空欄は \(\large{1\hspace{1pt}}\)番目の文字を除いた \(\large{\color{#e00d0d}{4}\hspace{1pt}}\)種類 から選びます。
右側の空欄は \(\large{1\hspace{1pt}}\)番目、\(\large{2\hspace{1pt}}\)番目の文字を除いた \(\large{\color{#e00d0d}{3}\hspace{1pt}}\)種類 から選びます。

よって、\(\large{5\hspace{1pt}}\)つの文字から \(\large{3\hspace{1pt}}\)つの文字を選んで並び替えたときの順列の数は $$\large{5 \times 4 \times 3 = 60}$$ から \(\large{60\hspace{1pt}}\)通り と求めることができます。

・順列の公式①

\(\large{n\hspace{1pt}}\)個のものから\(\large{r\hspace{1pt}}\)個を取り出して並べる順列の総数は以下のような公式により表されます。

順列の公式は『\(\large{{}_nP_r}\) は \(\large{n}\) から \(\large{1\hspace{1pt}}\)づつ数字を減らした数を \(\large{r\hspace{2pt}}\)個かけ算する』と覚えると簡単に覚えられます。

例えば、\(\large{{}_{5} \hspace{1pt}P_{\hspace{1pt}3}}\) の計算は \begin{eqnarray} \large {}_5 P_{\hspace{1pt}3} & \large = & \large 5 \times 4 \times 3 \\[0.7em] \large & \large = & \large 60 \\[0.7em] \end{eqnarray} となります。

つまり、\(\large{5}\) から\(\large{\hspace{2pt}1\hspace{1pt}}\)づつ数字を減らした数を\(\large{\hspace{2pt}3\hspace{2pt}}\)個かけ算する計算になります。

・順列の公式②

また、順列の公式を変形すると \begin{eqnarray} \large {}_n P_r & \large = & \large n\hspace{1pt}(n-1)\hspace{1pt}(n-2)\cdots\hspace{1pt}(n-r+1) \\[0.7em] \large & \large = & \large \frac{n\hspace{1pt}(n-1)\cdots\hspace{1pt}(n-r+1)(n-r)\cdots 2 \cdot 1}{(n-r)\cdots 2 \cdot 1} \\[0.7em] \large & \large = & \large \frac{n!}{(n-r)!} \\[0.7em] \end{eqnarray} となります。

公式②において \(\large{n=r}\) の場合は \(\large{0\hspace{1pt}! = 1}\) として \begin{eqnarray} \large {}_n P_n & \large = & \large \frac{n\hspace{1pt}!}{0\hspace{1pt}!} \\[0.7em] \large & \large = & \large n\hspace{1pt}! \\[0.7em] \end{eqnarray} と求めます。

・例題

順列の公式に以下の数字を当てはめて計算します。

例題(1)の解答

順列の公式に \(\large{n=4\hspace{1pt}}\), \(\large{r=3}\) を当てはめると \begin{eqnarray} \large {}_4 P_{\hspace{1pt}3} & \large = & \large 4 \times 3 \times 2 \\[0.7em] \large & \large = & \large 24 \\[0.7em] \end{eqnarray} と求められます。

例題(2)の解答

順列の公式に \(\large{n=7\hspace{1pt}}\), \(\large{r=4}\) を当てはめると \begin{eqnarray} \large {}_7 P_{\hspace{1pt}4} & \large = & \large 7 \times 6 \times 5 \times 4\\[0.7em] \large & \large = & \large 840\\[0.7em] \end{eqnarray} と求められます。

【3】順列の問題

本章では、順列に関連する問題と解き方について解説します。

解答と解説 : 問題1

解答と解説 : 問題2

解答と解説 : 問題3

解答と解説 : 問題4

解答と解説 : 問題5

問題1の解答 : 並び方の問題

問題(1)の解答

\(\large{\hspace{5pt}6\hspace{1pt}}\)人が一列に並ぶときの並び方とは、\(\large{6\hspace{1pt}}\)個の異なるものから\(\large{6\hspace{1pt}}\)個のものを取り並べる順列となります。

順列の公式より \begin{eqnarray} \large {}_6 P_{\hspace{1pt}6} & \large = & \large 6\times 5 \times 4 \times 3 \times 2 \times 1\\[0.7em] \large & \large = & \large 720\\[0.7em] \end{eqnarray} したがって、\(\large{720\hspace{1pt}}\)通りとなります。

問題(2)の解答

\(\large{\hspace{5pt}6\hspace{1pt}}\)人から代表と副代表を\(\large{1\hspace{1pt}}\)人ずつ選ぶときの選び方とは、\(\large{6\hspace{1pt}}\)個の異なるものから\(\large{2\hspace{1pt}}\)個を取り出し並べる順列となります。

順列の公式より \begin{eqnarray} \large {}_6 P_{\hspace{1pt}2} & \large = & \large 6\times 5 \\[0.7em] \large & \large = & \large 30\\[0.7em] \end{eqnarray} したがって、\(\large{30\hspace{1pt}}\)通りとなります。

問題2の解答 : 整数・偶数・奇数を作る

問題(1)の解答

\(\large{\hspace{5pt}5\hspace{1pt}}\)個の数字から\(\large{4\hspace{1pt}}\)個の数字を取り出して並べる順列の総数を求めます。

順列の公式より \begin{eqnarray} \large {}_5 P_{\hspace{1pt}4} & \large = & \large 5 \times 4 \times 3 \times 2 \\[0.7em] \large & \large = & \large 120\\[0.7em] \end{eqnarray} したがって、\(\large{120\hspace{1pt}}\)通りとなります。

問題(2)の解答

並び替えてできる数が偶数であるためには、一の位が \(\large{2\hspace{1pt}}\) か \(\large{4}\) のどちらかとなります。
つまり、一の位の数字は\(\large{\hspace{2pt}2\hspace{1pt}}\)通りとなります。

また、残りの\(\large{\hspace{2pt}3\hspace{1pt}}\)桁には一の位に使用した数字以外の\(\large{4\hspace{1pt}}\)つの数字が入ります。

つまり、\(\large{4\hspace{1pt}}\)桁の偶数の数は \begin{eqnarray} \large 2 \times {}_4 P_{\hspace{1pt}3} & \large = & \large 2\times 4 \times 3 \times 2 \\[0.7em] \large & \large = & \large 48\\[0.7em] \end{eqnarray} したがって、\(\large{48\hspace{1pt}}\)通りとなります。

問題(3)の解答

並び替えてできる数が奇数であるためには、一の位が \(\large{1\hspace{1pt},\hspace{2pt}3\hspace{1pt},\hspace{2pt}5}\) のどれかとなります。
つまり、一の位の数字は\(\large{\hspace{2pt}3\hspace{1pt}}\)通りとなります。

また、残りの\(\large{\hspace{2pt}2\hspace{1pt}}\)桁には一の位に使用した数字以外の\(\large{4\hspace{1pt}}\)つの数字が入ります。

つまり、\(\large{3\hspace{1pt}}\)桁の奇数の数は \begin{eqnarray} \large 3 \times {}_4 P_{\hspace{1pt}2} & \large = & \large 3\times 4 \times 3 \\[0.7em] \large & \large = & \large 36\\[0.7em] \end{eqnarray} したがって、\(\large{36\hspace{1pt}}\)通りとなります。

問題3の解答 : 0を含む数字の並び

問題(1)の解答

千の位の数は、\(\large{0\hspace{1pt}}\)以外の数字から選ぶため、\(\large{5\hspace{1pt}}\)通りとなります。

残りの\(\large{\hspace{2pt}3\hspace{1pt}}\)桁の数字の選び方は、千の位で使用した数字以外の\(\large{\hspace{5pt}5\hspace{1pt}}\)個の数字から\(\large{3\hspace{1pt}}\)個の数字を取り出して並べる順列から求めます。

順列の公式より \begin{eqnarray} \large 5 \times {}_5 P_{\hspace{1pt}3} & \large = & \large 5 \times 5 \times 4 \times 3 \\[0.7em] \large & \large = & \large 300\\[0.7em] \end{eqnarray} したがって、\(\large{300\hspace{1pt}}\)通りとなります。

問題(2)の解答

並び替えてできる数が奇数であるためには、一の位が\(\large{1\hspace{1pt},\hspace{2pt}3\hspace{1pt},\hspace{2pt}5}\) のどれかとなります。
つまり、一の位の数字は\(\large{3\hspace{1pt}}\)通りとなります。

また、千の位の数は \(\large{0\hspace{3pt}}\)と一の位で使用した数字以外から選ぶため、\(\large{4\hspace{1pt}}\)通りとなります。

残りの\(\large{\hspace{2pt}2\hspace{1pt}}\)桁では一の位、千の位に使用した数字以外の\(\large{4\hspace{1pt}}\)つの数字から\(\large{\hspace{2pt}2\hspace{1pt}}\)つを選びます。

つまり、\(\large{4\hspace{1pt}}\)桁の奇数の数は \begin{eqnarray} \large 3 \times 4 \times {}_4 P_{\hspace{1pt}2} & \large = & \large 3 \times 4 \times 4 \times 3 \\[0.7em] \large & \large = & \large 144\\[0.7em] \end{eqnarray} したがって、\(\large{144\hspace{1pt}}\)通りとなります。

問題(3)の解答

\(\large{430\hspace{1pt}}\)より大きい\(\large{3\hspace{1pt}}\)桁の数は \(\large{43〇\hspace{1pt},\hspace{2pt}45〇\hspace{1pt},\hspace{2pt}5〇〇\hspace{1pt}}\) の\(\large{\hspace{1pt}3\hspace{1pt}}\)つのパターンがあります。

【① \(\large{43〇}\) の場合】
　数字の並びが \(\large{43〇}\) である場合、\(\large{〇}\)は\(\large{\hspace{2pt}0\hspace{1pt},\hspace{2pt}3\hspace{1pt},\hspace{2pt}4\hspace{2pt}}\)を除いた\(\large{\hspace{2pt}1\hspace{1pt},\hspace{2pt}2\hspace{1pt},\hspace{2pt}5}\) の\(\large{\hspace{1pt}3\hspace{1pt}}\)個から選ぶため、\(\large{3\hspace{1pt}}\)通りとなります。

【② \(\large{45〇}\) の場合】
　数字の並びが \(\large{45〇}\) である場合、\(\large{〇}\)は \(\large{0\hspace{1pt},\hspace{2pt}1\hspace{1pt},\hspace{2pt}2\hspace{1pt},\hspace{2pt}3}\) の\(\large{4\hspace{1pt}}\)個から選ぶため、\(\large{4\hspace{1pt}}\)通りとなります。

【③ \(\large{5〇〇}\) の場合】
　数字の並びが \(\large{5〇〇}\) である場合、\(\large{〇〇}\)は \(\large{0\hspace{1pt},\hspace{2pt}1\hspace{1pt},\hspace{2pt}2\hspace{1pt},\hspace{2pt}3\hspace{1pt},\hspace{2pt}4}\) の\(\large{5\hspace{1pt}}\)個から\(\large{2\hspace{1pt}}\)個を選ぶため、\(\large{{}_5 P_{\hspace{1pt}2}}\) 通りとなります。

すなわち、①～③より \begin{eqnarray} \large 3 + 4 + {}_5 P_{\hspace{1pt}2} & \large = &\large 7 + 5 \times 4 \\[0.7em] \large & \large = & \large 27\\[0.7em] \end{eqnarray} したがって、\(\large{27\hspace{1pt}}\)通りとなります。

問題4の解答 : 隣り合う・交互に並ぶ・少なくとも一端の条件の並び方

問題(1)の解答 | 隣り合う並び方

隣り合う条件の順列の総数を求める場合は、隣り合うものを一組とみなします。
本問では、子供\(\large{3\hspace{1pt}}\)人を一組とみなして並び方を求めます。

大人\(\large{4\hspace{1pt}}\)人と子供一組の並び方は \(\large{{}_5 P_{\hspace{1pt}5}}\) となります。
また、子供\(\large{3\hspace{1pt}}\)人の組の中の並び方は \(\large{{}_3 P_{\hspace{1pt}3}}\) となります。

したがって、 \begin{eqnarray} \large {}_5 P_{\hspace{1pt}5}\times {}_3 P_{\hspace{1pt}3} & \large = &\large 120\times 6 \\[0.7em] \large & \large = & \large 720\\[0.7em] \end{eqnarray} すなわち、\(\large{720\hspace{1pt}}\)通りとなります。

問題(2)の解答 | 両端に条件がある場合

まず、大人\(\large{4\hspace{1pt}}\)人のうち \(\large{2\hspace{1pt}}\)人が両端となる選び方は \(\large{{}_4 P_{\hspace{1pt}2}}\) 通りとなります。
次に、残りの\(\large{5\hspace{1pt}}\)人が間に並ぶと考えると、その並び方は \(\large{{}_5 P_{\hspace{1pt}5}}\) 通りとなります。

したがって、 \begin{eqnarray} \large {}_4 P_{\hspace{1pt}2}\times {}_5 P_{\hspace{1pt}5} & \large = &\large 12\times 120 \\[0.7em] \large & \large = & \large 1440\\[0.7em] \end{eqnarray} すなわち、\(\large{1440\hspace{1pt}}\)通りとなります。

問題(3)の解答 | 交互に並ぶ場合

大人と子供が交互に並ぶ場合、大人\(\large{4\hspace{1pt}}\)人の間に子供が並ぶ『大小大小大小大』という並び方に限られます。
このような順列を考える場合は、先に大人\(\large{4\hspace{1pt}}\)人を並べ、その間に子供\(\large{3\hspace{1pt}}\)人を並べると考えます。

まず、大人\(\large{4\hspace{1pt}}\)人の並び方は \(\large{{}_4 P_{\hspace{1pt}4}}\) となります。
次に、その間に残りの子供\(\large{3\hspace{1pt}}\)人を並べると考えると、その並べ方は \(\large{{}_3 P_{\hspace{1pt}3}}\) 通りとなります。

したがって \begin{eqnarray} \large {}_4 P_{\hspace{1pt}4}\times {}_3 P_{\hspace{1pt}3} & \large = &\large 24 \times 6 \\[0.7em] \large & \large = & \large 144\\[0.7em] \end{eqnarray} すなわち、\(\large{144\hspace{1pt}}\)通りとなります。

問題(4)の解答 | "少なくとも一端"に条件がある場合

並び方の少なくとも一端に条件がある場合は、並び方の余事象を考えると計算が簡単になります。

問題の『少なくとも一端に子供がいる』並び方の余事象は、『両端に大人がいる』となります。

つまり、\(\large{7\hspace{1pt}}\)人の並び方の数から両端に大人がいる並び方の数を引くことで、少なくとも一端に子供のいる並び方が計算されます。

まず、\(\large{7\hspace{1pt}}\)人の並び方は \(\large{{}_7 P_{\hspace{1pt}7}}\) となります。

次に、大人\(\large{4\hspace{1pt}}\)人のうち \(\large{2\hspace{1pt}}\)人が両端となる並び方は \(\large{{}_4 P_{\hspace{1pt}2}}\) となります。
また、残りの\(\large{5\hspace{1pt}}\)人の並び方は \(\large{{}_5 P_{\hspace{1pt}5}}\) となります。

したがって、 \begin{eqnarray} \large {}_7 P_{\hspace{1pt}7}- ( {}_4 P_{\hspace{1pt}2} \times {}_5 P_{\hspace{1pt}5})& \large = &\large 5040 -(12 \times 120) \\[0.7em] \large & \large = & \large 3600\\[0.7em] \end{eqnarray} すなわち、\(\large{3600\hspace{1pt}}\)通りとなります。

問題5の解答 : 交互に並ぶ並び方

問題の解答 | 隣り合う並び方

問題4の(3)では、大人\(\large{4\hspace{1pt}}\)人と子供\(\large{3\hspace{1pt}}\)人が交互に並ぶことで『大小大小大小大』というパターンに限られました。

一方、本問では 大人\(\large{3\hspace{1pt}}\)人、子供\(\large{3\hspace{1pt}}\)人が一列に並ぶため『大小大小大小』と『小大小大小大』の "2つのパターンが存在する" 点に注意が必要です。

【左側に大人がいる場合】
　大人\(\large{3\hspace{1pt}}\)人の並び方の数は \(\large{{}_3 P_{\hspace{1pt}3}}\) となります。
　また、大人の右隣に子供\(\large{3\hspace{1pt}}\)人を並べると考えると、その並び方の数は \(\large{{}_3 P_{\hspace{1pt}3}}\) となります。

　すなわち、左側に大人がいる場合の並び方は \(\large{{}_3 P_{\hspace{1pt}3} \times {}_3 P_{\hspace{1pt}3}}\) となります。

【左側に子供がいる場合】
　子供\(\large{3\hspace{1pt}}\)人の並び方の数は \(\large{{}_3 P_{\hspace{1pt}3}}\) となります。
　また、子供の右隣に大人\(\large{3\hspace{1pt}}\)人を並べると考えると、その並び方の数は \(\large{{}_3 P_{\hspace{1pt}3}}\) となります。

　すなわち、左側に子供がいる場合の並び方は \(\large{{}_3 P_{\hspace{1pt}3} \times {}_3 P_{\hspace{1pt}3}}\) となります。

以上から、大人\(\large{3\hspace{1pt}}\)人と子供\(\large{3\hspace{1pt}}\)人が交互に並ぶ並び方は \begin{eqnarray} \large 2 \times {}_3 P_{\hspace{1pt}3} \times {}_3 P_{\hspace{1pt}3} & \large = &\large 2 \times 6 \times 6\\[0.7em] \large & \large = & \large 72\\[0.7em] \end{eqnarray} すなわち、\(\large{72\hspace{1pt}}\)通りとなります。

---