円順列・じゅず順列 | 問題と解き方

本項では以下の内容を解説しています。

• ・円順列の公式
• ・じゅず順列の公式
• ・問題の一覧

【1】円順列

円順列とは、複数のものを円形に並べたときの配列のことをいいます。

順列は複数のものを一列に並べたときの並べ方を求める計算でした。

一方、円順列は複数のものを円形に並べたときの数であるため、回転して重複しないように並べ方の数を求める必要があります。

例えば \(\large{\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt},\hspace{1pt}D\hspace{1pt}}\) の\(\large{\hspace{1pt}4\hspace{1pt}}\)つの文字を円形に並べる並べ方を例に円順列を考えます。

・円順列の例題

\(\large{\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt},\hspace{1pt}D\hspace{1pt}}\) の\(\large{\hspace{1pt}4\hspace{1pt}}\)つの文字を一列に並べる並べ方は順列の公式から \(\large{\hspace{1pt}{}_4 P_4=4\hspace{1pt}!\hspace{2pt}}\)通り となります。

ここで、一列に並んだ文字の両端をつなぎ合わせ、文字を円形に並べると、以下のような並べ方は回転することで同じ並べ方となります。

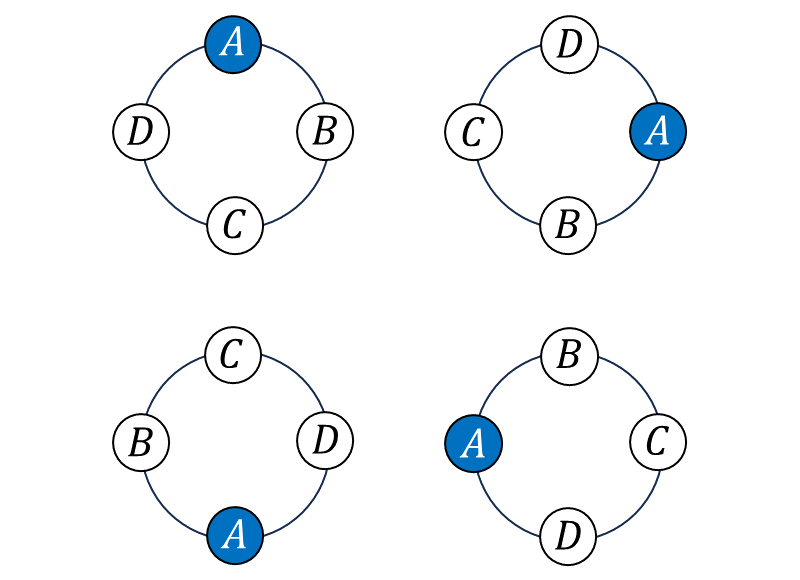
よって、円形に並べる並べ方の総数を求める場合は、回転して同じ並べ方となるものを数えないようにする必要があります。

そこで、以下の図のように ある一つの文字を固定し、残りの\(\large{\hspace{1pt}3\hspace{1pt}}\)つの場所に文字を配置すると考えます。

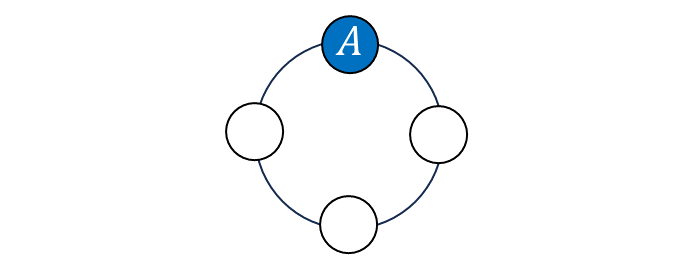
このように考えると、\(\large{\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt},\hspace{1pt}D\hspace{1pt}}\) の\(\large{\hspace{1pt}4\hspace{1pt}}\)つの文字を円形に並べる並べ方は \begin{eqnarray} \large \hspace{1pt}(4-1)\hspace{1pt}!& \large = & \large 3\hspace{1pt}!\\[0.7em] \large & \large = & \large 3\cdot 2\cdot 1\\[0.7em] \large & \large = & \large 6\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}4\hspace{1pt}}\)つの文字を円形に並べる並べ方は\(\large{\hspace{1pt}6\hspace{1pt}}\)通りとなります。

・円順列の公式

一般的には、異なる\(\large{n\hspace{1pt}}\)個のものを円形に配置する並べ方の数は以下の公式で表されます。

・例題

円順列の公式から \begin{eqnarray} \large \hspace{1pt}(6-1)\hspace{1pt}!& \large = & \large 5\hspace{1pt}!\\[0.7em] \large & \large = & \large 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\\[0.7em] \large & \large = & \large 120\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}6\hspace{1pt}}\)つの文字を円形に並べる並べ方は\(\large{\hspace{1pt}120\hspace{1pt}}\)通りとなります。

【2】じゅず順列

円順列では、異なるものを円形に配置したときに、回転により重複しないように並べ方を求めました。

ここで、玉に糸を通して輪を作った場合などでは、回転に加え、表裏を反対にしたときに重複しないように並べ方を求める必要があります。

表裏の重複も考慮する円順列をじゅず順列といいます。

例えば \(\large{\hspace{1pt}A\hspace{1pt},\hspace{1pt}B\hspace{1pt},\hspace{1pt}C\hspace{1pt},\hspace{1pt}D\hspace{1pt}}\) の\(\large{\hspace{1pt}4\hspace{1pt}}\)つの名前の付いた玉に糸を通して輪を作った じゅず順列 について考えます。

・じゅず順列の例

円順列では、ある一つの文字を固定し、残りの\(\large{\hspace{1pt}3\hspace{1pt}}\)つの場所に文字を配置すると考えました。

この円順列の求め方では、下の図のように表裏を反対にしたときに重複するパターンも数えてしまいます。

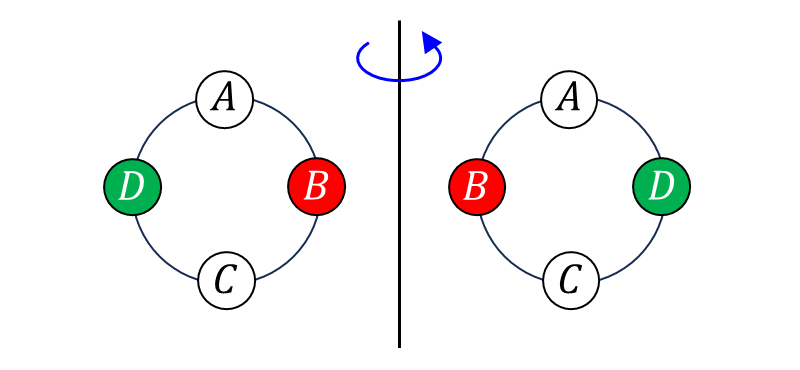
そのため、じゅず順列では表裏を反対にしたときに重複しないように、円順列から求められる並べ方を\(\large{\hspace{1pt}2\hspace{1pt}}\)で割り計算します。

すなわち、\(\large{\hspace{1pt}4\hspace{1pt}}\)つの名前の付いた玉に糸を通して輪を作るときは、以下のように求めます。 \begin{eqnarray} \large \hspace{1pt}\frac{(4-1)\hspace{1pt}!}{2}& \large = & \large \frac{3\hspace{1pt}!}{2}\\[0.7em] \large & \large = & \large \frac{3 \cdot 2 \cdot 1}{2}\\[0.7em] \large & \large = & \large 3\\[0.7em] \end{eqnarray} したがって、例題の並べ方は\(\large{\hspace{1pt}3\hspace{1pt}}\)通りと求められます。

・じゅず順列の公式

一般的には、異なる\(\large{n\hspace{1pt}}\)個のものを円形に配置し、表裏を反対にして重複するものを除いた並べ方の数は以下の公式で表されます。

・例題

じゅず順列の公式から \begin{eqnarray} \large \frac{(6-1)\hspace{1pt}!}{2}& \large = & \large \frac{5\hspace{1pt}!}{2}\\[0.7em] \large & \large = & \large \frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2}\\[0.7em] \large & \large = & \large 60\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}6\hspace{1pt}}\)つの名前の付いた玉に糸を通して輪を作るとき、玉の並べ方は \(\large{\hspace{1pt}60\hspace{1pt}}\)通りとなります。

【3】円順列・じゅず順列の問題

本章では、円順列・じゅず順列に関連する問題と解き方について解説します。

解答と解説 : 問題1

解答と解説 : 問題2

解答と解説 : 問題3

解答と解説 : 問題4

問題1の解答 : 円順列とじゅず順列の問題

問題(1)の解答

問題(1)と(2)は、同じ数の玉を使っていても 机の上に円形に並べる か 糸につないで輪にするか で数え方が異なる点に注意が必要です。

問題(1)は、机の上に玉を円形に並べるので円順列の問題です。

円順列の公式から \begin{eqnarray} \large \hspace{1pt}(7-1)\hspace{1pt}!& \large = & \large 6\hspace{1pt}!\\[0.7em] \large & \large = & \large 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\\[0.7em] \large & \large = & \large 720\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}7\hspace{1pt}}\)つの異なる玉を円形に並べる並べ方は\(\large{\hspace{1pt}720\hspace{1pt}}\)通りとなります。

問題(2)の解答

問題(2)は、玉を糸につないで輪にするため、表裏を反転したときに重複があります。
そのため、じゅず順列の公式を使用して計算します。

じゅず順列の公式から \begin{eqnarray} \large \frac{(7-1)\hspace{1pt}!}{2}& \large = & \large \frac{6\hspace{1pt}!}{2}\\[0.7em] \large & \large = & \large \frac{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2}\\[0.7em] \large & \large = & \large 360\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}7\hspace{1pt}}\)つの異なる玉を糸につないで輪にする方法は\(\large{\hspace{1pt}360\hspace{1pt}}\)通りとなります。

問題2の解答 : 向かい合う・隣り合う問題

問題(1)の解答 | 向かい合う問題

問題(1)は円形に座る方法の数を求める問題であるため、円順列の問題です。

円順列では\(\large{\hspace{2pt}1\hspace{1pt}}\)人の位置を固定し、残りの位置に他の人を並べると考えました。

本問では、子供\(\large{\hspace{1pt}2\hspace{1pt}}\)人が向かい合うという条件のため、子供\(\large{\hspace{1pt}1\hspace{1pt}}\)人を固定し、その向かい合う席にもう\(\large{\hspace{1pt}1\hspace{1pt}}\)人の子供が座ると考えます。

このように固定すると、残りの\(\large{4\hspace{1pt}}\)つの位置に大人\(\large{\hspace{1pt}4\hspace{1pt}}\)人を並べることになるため、順列の公式より \begin{eqnarray} \large 4\hspace{1pt}! & \large = & \large 4 \cdot 3 \cdot 2 \cdot 1 \\[0.7em] \large & \large = & \large 24\\[0.7em] \end{eqnarray} したがって、\(\large{24\hspace{1pt}}\)通りとなります。

問題(2)の解答 | 隣り合う問題

本問では、隣り合う子供\(\large{\hspace{1pt}2\hspace{1pt}}\)人を\(\large{\hspace{1pt}1\hspace{1pt}}\)つの組と考えて、大人\(\large{\hspace{1pt}4\hspace{1pt}}\)人と子供\(\large{\hspace{1pt}1\hspace{1pt}}\)組の円順列を求めます。

大人\(\large{\hspace{1pt}4\hspace{1pt}}\)人と子供\(\large{\hspace{1pt}1\hspace{1pt}}\)組が円形に座る並び方は \(\large{\hspace{1pt}(5-1)\hspace{1pt}!\hspace{1pt}=4\hspace{1pt}!\hspace{1pt}}\)通りあります。

また、そのおのおのに対して子供\(\large{\hspace{1pt}2\hspace{1pt}}\)人の座り方が \(\large{\hspace{1pt}2\hspace{1pt}}\)通りあります。

つまり、子供\(\large{\hspace{1pt}2\hspace{1pt}}\)人が隣り合う座り方は \begin{eqnarray} \large \hspace{1pt}(5-1)\hspace{1pt}! \times 2 & \large = & \large 4\hspace{1pt}! \times 2\\[0.7em] \large & \large = & \large 4 \cdot 3 \cdot 2 \cdot 1 \times 2\\[0.7em] \large & \large = & \large 48\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}48\hspace{1pt}}\)通りとなります。

問題(3)の解答 | 隣り合わずに座る

本問のように隣り合わない条件の座り方を求める場合は、(全体の数)-(隣り合って座る) を計算すると簡単に求められます。

\(\large{\hspace{1pt}6\hspace{1pt}}\)人が円形に座る方法の数は円順列の公式から \begin{eqnarray} \large(6-1)\hspace{1pt}! & \large = & \large 5\hspace{1pt}!\\[0.7em] \large & \large = & \large 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \\[0.7em] \large & \large = & \large 120\\[0.7em] \end{eqnarray} したがって、\(\large{\hspace{1pt}120\hspace{1pt}}\)通りとなります。

また、問題(2)から子供\(\large{\hspace{1pt}2\hspace{1pt}}\)人が隣り合う座り方は\(\large{\hspace{1pt}48\hspace{1pt}}\)通りです。

したがって、 $$\large{120-48 = 72}$$ したがって、子供\(\large{\hspace{1pt}2\hspace{1pt}}\)人が隣り合わない座り方は\(\large{\hspace{1pt}72\hspace{1pt}}\)通りです。

問題3の解答 : 交互に座る問題

問題(4)の解答 | 交互に座る問題

問題(4)のように大人と子供が交互に座る場合は、まず大人\(\large{\hspace{1pt}4\hspace{1pt}}\)人の位置を決めてから、大人の間に子供が座ると考えます。

大人\(\large{\hspace{1pt}1\hspace{1pt}}\)人の位置を固定して、残りの大人\(\large{\hspace{1pt}3\hspace{1pt}}\)人が円形に座る方法は、円順列の公式から $$\large{(4-1)\hspace{1pt}! = 3\hspace{1pt}!}$$ となります。

また、大人の間の\(\large{\hspace{1pt}4\hspace{1pt}}\)つの位置に子供\(\large{\hspace{1pt}4\hspace{1pt}}\)人を並べると考える方法は、順列の公式より $$\large{4\hspace{1pt}!}$$ となります。(すでに、大人\(\large{\hspace{1pt}1\hspace{1pt}}\)人の位置を固定しているため、円順列ではなく順列で計算します。)

以上から、 \begin{eqnarray} \large 4\hspace{1pt}! \times 3\hspace{1pt}! & \large = & \large 4 \cdot 3 \cdot 2 \cdot 1 \times 3 \cdot 2 \cdot 1 \\[0.7em] \large & \large = & \large 144\\[0.7em] \end{eqnarray}

したがって、大人\(\large{\hspace{1pt}4\hspace{1pt}}\)人と子供\(\large{\hspace{1pt}4\hspace{1pt}}\)人が円形に座るとき、交互に座る方法は\(\large{144\hspace{1pt}}\)通りとなります。

問題4の解答 : 選んでから円形に配置する問題

問題(1)の解答 | 全体から選んで円形に配置する問題

この問題は、全体からある人数を選んでから円形に配置する問題です。

円順列の公式は全てのものを円形に並べるときの公式であるため、公式がそのまま使えない点に注意が必要です。

まず、\(\large{\hspace{1pt}10\hspace{1pt}}\)人から\(\large{\hspace{1pt}5\hspace{1pt}}\)人を選び、一列に並んだ\(\large{\hspace{1pt}5\hspace{1pt}}\)つの席に座る方法は \(\large{{}_{10} P_5 \hspace{2pt}}\)通りあります。

席の両端をつなぎ円形に配置すると、席が一列のときの並び方それぞれに対し、回転して同じ並びとなる並び方が\(\large{\hspace{1pt}5\hspace{1pt}}\)通りずつあります。

したがって、 \begin{eqnarray} \large {}_{10} P_5 \div 5 & \large = & \large \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 }{5} \\[0.7em] \large & \large = & \large 6048\\[0.7em] \end{eqnarray} 以上から、\(\large{\hspace{1pt}10\hspace{1pt}}\)人から\(\large{\hspace{1pt}5\hspace{1pt}}\)人を選んで円形に並んで座る方法は\(\large{\hspace{1pt}6048\hspace{1pt}}\)通りとなります。

---