三角方程式の解の個数
本項では、『三角方程式の解の個数』の解法について解説します。
【1】基本的な三角方程式の解の個数
三角方程式の解の個数を求める問題とは、 $$\displaystyle \large{\sin^2 \theta + \sin\theta = a}$$ など三角方程式に対して 定数\(\large{a}\) の値により解の個数を求める問題です。
本項では、以下の(1),(2)の三角方程式の解き方について解説します。
\(\displaystyle \large{(1)\hspace{20pt}\sin \theta = a\hspace38pt}\)
\(\displaystyle \large{(2)\hspace{5pt}\cos^2 \theta + \sin \theta=2-a}\)
問題(1) sinθ=a の解の個数
まず、以下の三角方程式の解の個数について調べます。
\(\displaystyle \large{\sin \theta = a}\)
三角方程式の解の個数を調べるときは、定数分離がよく用いられます。
\(\large{y=f(x)}\) と \(\large{y=a}\) の交点と一致する
方程式 \(\large{f(x)=a}\) は定数\(\large{a}\) により関数が変化してしまいます。
一方、定数分離を利用して \(\large{y=f(x)}\) と \(\large{y=a}\) に分離することで、\(\large{f(x)}\) を定数\(\large{a}\) に依存しない式に分離できるため、見通しが良くなります。
定数分離を使用すると、『\(\large{\sin \theta = a}\)』の解は、\(\large{y=\sin \theta}\) と \(\large{y=a}\) の交点から求めることができます。
\(\large{y=\sin \theta}\) と \(\large{y=a}\) の交点の考え方は 『①単位円』を使用する場合と、『②三角関数のグラフ』を使用する場合とで分けられますが、どちらも結果は同じになります。
解法① : 単位円と解の個数
三角関数の定義から 単位円において \(\large{\sin \theta}\) は動径の\(\large{y}\)座標の値に等しくなります。
つまり、単位円に直線 \(\large{y=a}\) を書き、単位円との交点の数を調べると、 『\(\large{y=\sin \theta}\)』と『\(\large{y=a}\)』 の解の個数を求めることができます。
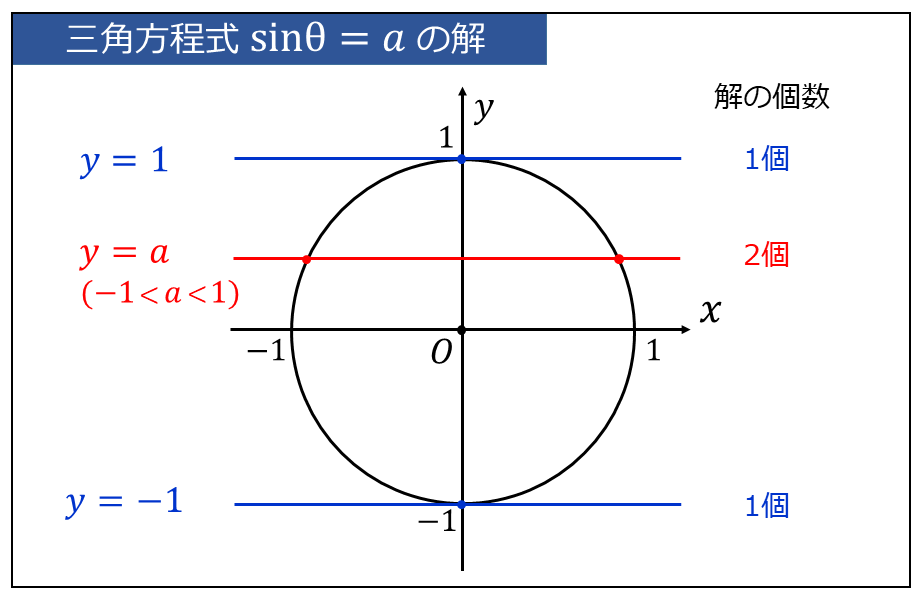
上図から、問題の \(\large{\sin \theta = a}\) の解の個数は、以下のようになります。
| \(\large{a}\) の範囲 | 解\(\large{\theta}\)の個数 |
|---|---|
| \(\displaystyle \large{a>1,\hspace{3pt}a<-1}\) | 0個 |
| \(\displaystyle \large{a=\pm1}\) | 1個 |
| \(\displaystyle \large{-1 < a < 1}\) | 2個 |
解法② : グラフと解の個数
先述した解法では、三角関数の定義を利用して 単位円と直線の交点から解の個数を求めました。
一方、三角関数のグラフ と 直線の交点 から解の個数を求めることもできます。
三角関数のグラフから、\(\large{y=\sin \theta}\) を描いた図を下に示します。
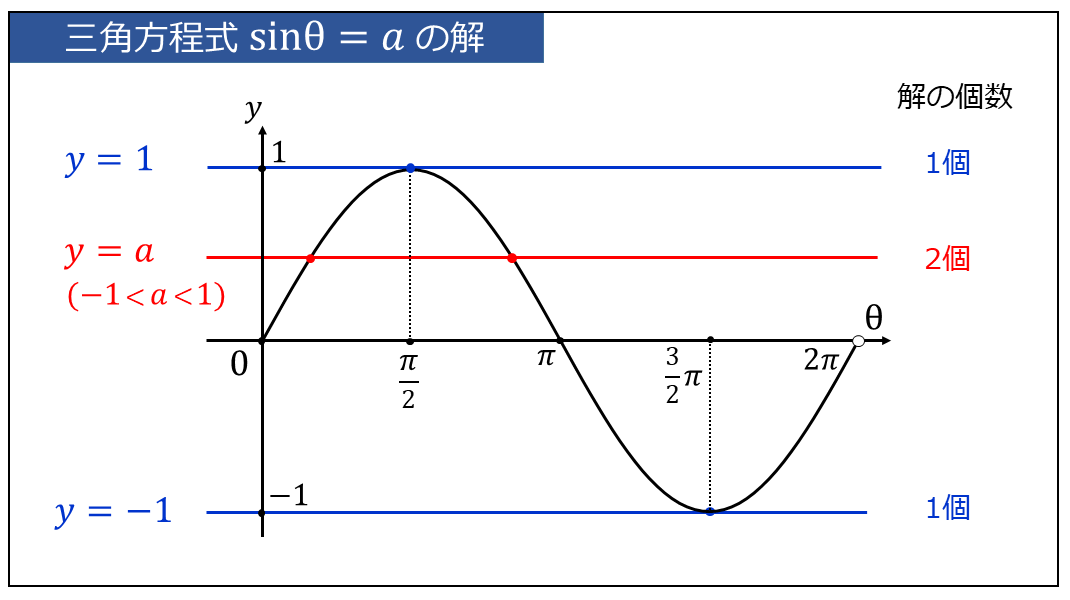
上図から、問題の \(\large{\sin \theta = a}\) の解の個数は、以下のようになります。
| \(\large{a}\) の範囲 | 解\(\large{\theta}\)の個数 |
|---|---|
| \(\displaystyle \large{a>1,\hspace{3pt}a<-1}\) | 0個 |
| \(\displaystyle \large{a=\pm1}\) | 1個 |
| \(\displaystyle \large{-1 < a < 1}\) | 2個 |
【2】置換による解の個数の解法
次に、以下の三角方程式の解の個数の問題について考えます。
\(\displaystyle \large{\cos^2 \theta + \sin \theta =2-a}\)
まず、与えられた問題は \(\large{\sin}\) と \(\large{\cos}\) がそろっていないため、相互関係の式から変形します。
三角関数の相互関係から、 $$\large{\sin^2 \theta + \cos^2 \theta = 1}$$ となります。問題の式を変形すると、 $$\large{\cos^2 \theta + \sin \theta =2-a}$$ $$\large{(1-\sin^2 \theta)+ \sin \theta=2-a}$$ $$\large{\sin^2 \theta -\sin \theta +1 =a}$$ と変形されます。
ここで、\(\large{\sin \theta = x}\) と置換すると、\(\large{0 \leqq \theta < 2\pi }\) より、\(\large{-1 \leqq x \leqq 1 }\) となります。
与えられた方程式は、 $$\large{x^2 - x +1 = a}$$ となります。ここで、定数分離により 『\(\large{y=x^2 - x +1 }\)』 と 『\(\large{y=a}\)』 の交点を求めることで、解の個数を求めます。
ここで、\(\large{y= x^2 - x +1}\) を 平方完成すると、以下のようになります。 $$\displaystyle \large{y= \left(x-\frac{1}{2}\right)^2 + \frac{3}{4}}$$
これより、\(\large{y=x^2 - x +1}\) と \(\large{y=a}\) をグラフに書くと以下になります。
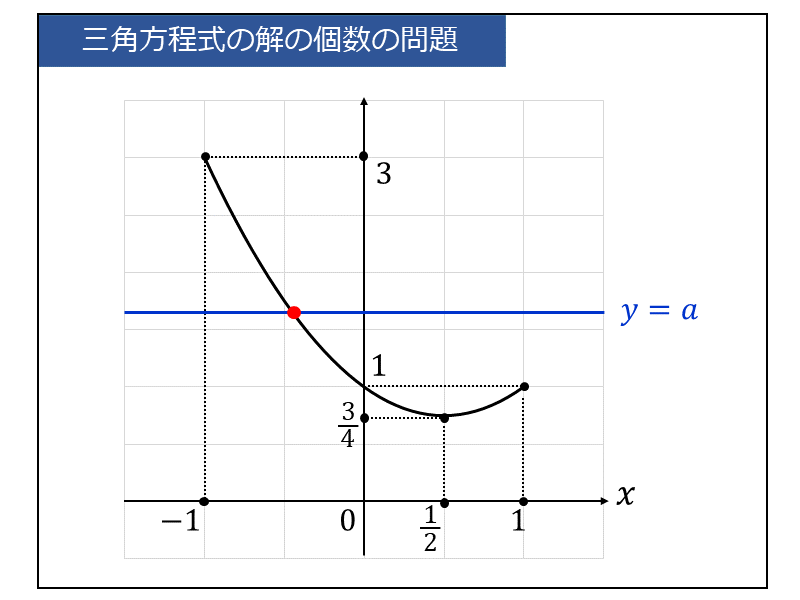
上図から、\(\large{a}\) の値を変化させたときの \(\large{y=x^2 - x +1 }\) と \(\large{y=a}\) の交点の数を整理すると、以下のようになります。
| \(\large{a}\) の範囲 | 交点の個数 |
|---|---|
| \(\displaystyle \large{a > 3,\hspace{3pt}a < \frac{3}{4}}\) | 0個 |
| \(\displaystyle \large{1 < a \leqq 3, \hspace{3pt}a = \frac{3}{4}}\) | 1個 |
| \(\displaystyle \large{\frac{3}{4} < a \leqq 1}\) | 2個 |
ここで、上記の交点の数とは、\(\large{x^2 - x +1 = a}\) の 解\(\large{x}\) の個数を意味します。
一方、求めたい解の個数は、\(\large{\sin \theta = x}\) を満たす解\(\large{\theta}\) の数です。
そこで、前章の問題(1)で求められた結果を利用して、解\(\large{x}\) に対応する 解\(\large{\theta}\) の個数を求めます。
問題(1)から \(\large{\sin \theta = x}\) における \(\large{x}\) の範囲に対する 解\(\large{\theta}\) の個数を以下の表に示します。
| \(\large{x}\) の範囲 | 解\(\large{\theta}\) の個数 |
|---|---|
| \(\displaystyle \large{x>1,\hspace{3pt}x<-1}\) | 0個 |
| \(\displaystyle \large{x=\pm1}\) | 1個 |
| \(\displaystyle \large{-1 < x < 1}\) | 2個 |
上記の結果を利用して、定数\(\large{a}\) の値に対する 解\(\large{\theta}\) の個数を求めます。
例として、『\(\large{a=3}\)』 と 『\(\large{a=1}\)』の解の個数の求め方について解説します。
・a=3 の解の個数
\(\large{a=3}\) のときの解の個数を求めます。
下図には、\(\large{a=3}\) のときの \(\large{y=x^2 - x +1 }\) と \(\large{y=a}\) のグラフを書いています。
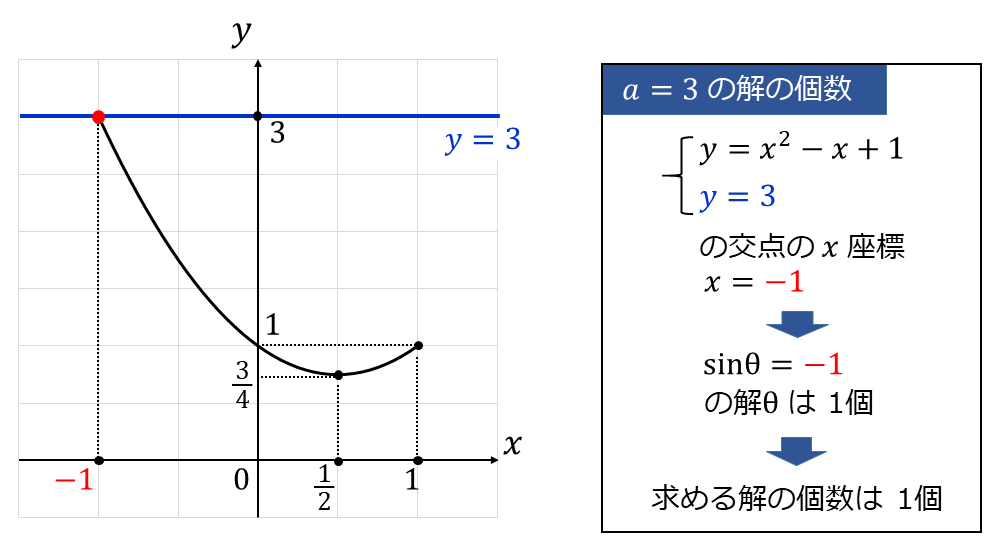
上図から、\(\large{a=3}\) のとき \(\large{y=x^2 - x +1 }\) と \(\large{y=a}\) の交点は1つであり、その交点の \(\large{x}\)座標は \(\large{x=\color{red}{-1}}\) です。
ここで、 \(\large{x=\color{red}{-1}}\) のとき \(\large{0 \leqq \theta < 2\pi }\) における \(\large{\sin \theta = x}\) の 解\(\large{\theta}\) の個数は1個です。
したがって、求める解の個数は 1個 になります。
・a=1 の解の個数
また、\(\large{a=1}\) のときの解の個数を求めます。
下図には、\(\large{a=1}\) のときの \(\large{y=x^2 - x +1 }\) と \(\large{y=a}\) のグラフを書いています。
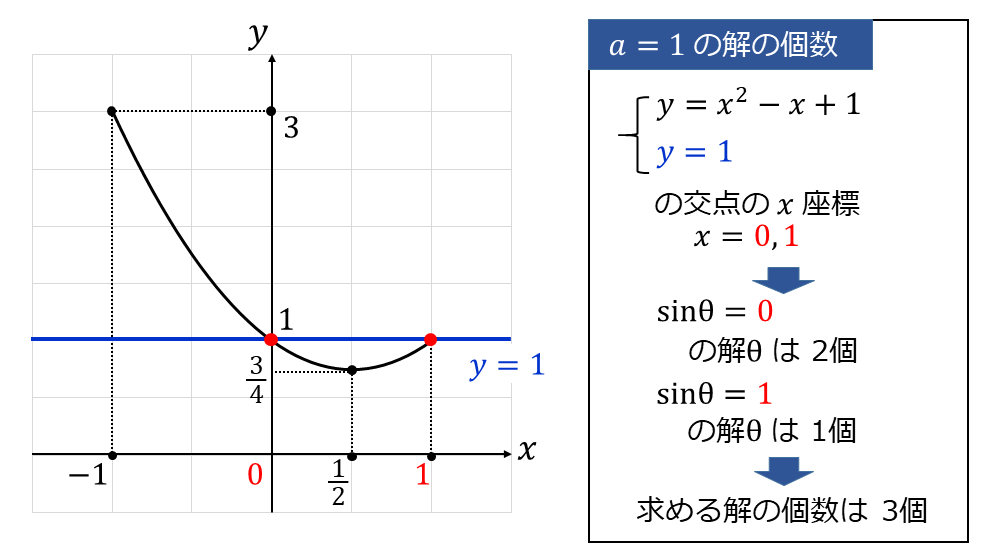
上図から、\(\large{a=1}\) のとき \(\large{y=x^2 - x +1 }\) と \(\large{y=a}\) の交点は2つであり、その交点の \(\large{x}\)座標は \(\large{x=\color{red}{0,\hspace{2pt}1}}\) です。
ここで、\(\large{0 \leqq \theta < 2\pi }\) における \(\large{x=\color{red}{0}}\) のときの \(\large{\sin \theta = x}\) の解の個数は2個、
\(\large{x=\color{red}{1}}\) のときの \(\large{\sin \theta = x}\) の解の個数は1個です。
したがって、求める解の個数は 3個 になります。
・解の個数の計算結果
以上のように、定数\(\large{a}\) を変化させたときの 解\(\large{\theta}\) の数をまとめると、以下のようになります。
| \(\large{a}\) の範囲 | 解\(\large{\theta}\) の個数 |
|---|---|
| \(\displaystyle \large{a>3,\hspace{3pt}a<\frac{3}{4}}\) | 0個 |
| \(\displaystyle \large{a=3}\) | 1個 |
| \(\displaystyle \large{1< a < 3,\hspace{3pt}a=\frac{3}{4}}\) | 2個 |
| \(\displaystyle \large{a=1}\) | 3個 |
| \(\displaystyle \large{\frac{3}{4} < a < 1}\) | 4個 |