三角関数の合成 | 証明と問題

本項では、三角関数の合成 について解説します。

【1】三角関数の合成 | 公式の証明

三角関数の合成とは、\(\displaystyle \large{a\sin\theta+b\cos\theta}\) で表される三角関数を、\(\displaystyle \large{r\sin(\theta+\alpha)}\) の式に変形する方法のことをいいます。

三角関数の合成は、\(\large{\sin}\) の加法定理 $$\large{\sin(\theta + \alpha) = \sin \theta \cos \alpha + \cos \theta \sin \alpha}$$ から導くことができます。

・公式の証明 | sinに合成

三角関数の合成の公式を証明します。

まず、合成の式の左辺から \(\large{\sqrt{a^2+b^2}}\) をくくり出します。

\begin{eqnarray} &&\large a\sin\theta+b\cos\theta\\[0.5em] &\large =&\large \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin\theta + \frac{b}{\sqrt{a^2+b^2}}\cos\theta\right)\\[0.5em] \end{eqnarray} ここで、\(\large{r=\sqrt{a^2+b^2}}\) とおくと、 \begin{eqnarray} & &\large \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin\theta + \frac{b}{\sqrt{a^2+b^2}}\cos\theta\right)\\[0.5em] &\large =&\large r\left(\sin\theta\cdot\frac{a}{r} +\cos\theta\cdot \frac{b}{r}\right)\\[0.5em] \end{eqnarray} となります。

ここで、角度\(\large{\alpha}\) が \(\displaystyle\large{\sin \alpha = \frac{b}{r}\hspace{1pt}, \hspace{3pt}}\)\(\displaystyle\large{\cos \alpha = \frac{a}{r}}\) を満たすとすると、 \begin{eqnarray} & &\large r\left(\sin\theta\cdot\frac{a}{r} +\cos\theta\cdot \frac{b}{r}\right)\\[0.5em] &\large =&\large r\left(\sin\theta\cos \alpha +\cos\theta\sin \alpha\right)\\[0.5em] &\large =&\large r\sin(\theta +\alpha)\\[0.5em] \end{eqnarray} と合成の式を導くことができます。

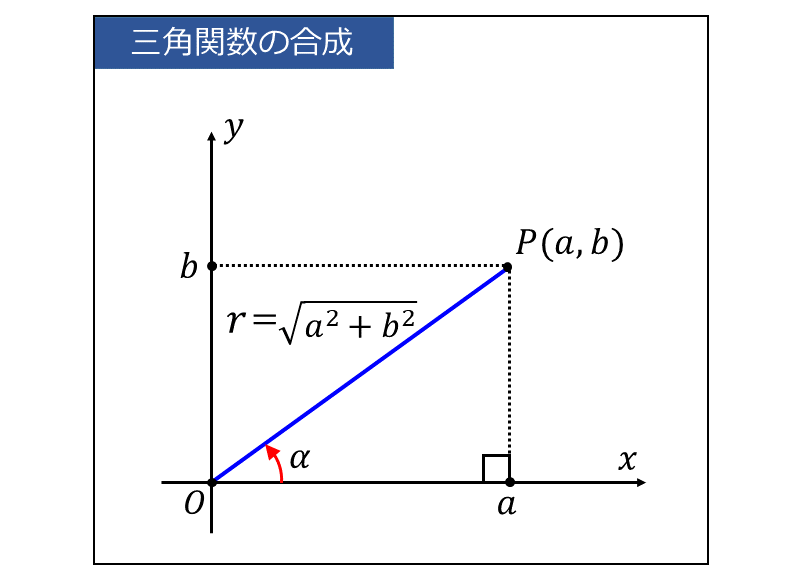
証明の途中で定義した角度\(\large{\alpha}\) とは、以下の図のように 原点\(\large{O}\) と 座標\(\large{(a,\hspace{1pt}b)}\) の点\(\large{P}\) を結んだ線分\(\large{\overline{OP}}\) に対して、\(\large{x}\)軸の正の部分から反時計回りに計る角度となります。

・公式の証明 | cosに合成

三角関数の合成は、\(\large{\cos(\theta+\alpha)}\) に合成することもできます。

\(\large{\cos(\theta+\beta)}\) に合成する場合は、\(\large{\cos}\) の加法定理 $$\large{\cos(\theta + \beta) = \cos \theta \cos \beta - \sin \theta \sin \beta}$$ から導くことができます。

\(\large{\sin}\) の場合と同様に、左辺を \(\large{r=\sqrt{a^2+b^2}}\) でくくり出すと、

\begin{eqnarray} &&\large a\sin\theta+b\cos\theta\\[0.5em] &\large =&\large \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin\theta + \frac{b}{\sqrt{a^2+b^2}}\cos\theta\right)\\[0.5em] &\large =&\large r\left(\sin\theta\cdot\frac{a}{r} +\cos\theta\cdot \frac{b}{r}\right)\\[0.5em] \end{eqnarray} となります。

ここで、角度\(\large{\beta}\) が \(\displaystyle\large{\sin \beta =-\frac{a}{r}\hspace{1pt}, \hspace{3pt}}\)\(\displaystyle\large{\cos \beta = \frac{b}{r}}\) を満たすとすると、 \begin{eqnarray} & &\large r\left(\sin\theta\left(-\sin \beta\right) +\cos\theta\cos \beta\right)\\[0.5em] &\large =&\large r\left(\cos\theta\cos \beta - \sin\theta\sin \beta\right)\\[0.5em] &\large =&\large r\cos(\theta +\beta)\\[0.5em] \end{eqnarray} と \(\large{\cos}\) の合成の式を導くことができます。

【2】基礎的な問題と解き方

三角関数の合成を利用した基礎的な問題について解説します。

問題(1)、問題(2)、問題(3)は 三角関数の合成により \(\large{\sin}\) に変形する問題です。

問題(4)は 三角関数の合成により \(\large{\cos}\) に変形する問題です。

問題(1) 三角関数の合成 | sinに変形

【解答と解説】

三角関数の合成の公式から、 $$\large{a \sin \theta + b \cos \theta = r \sin (\theta + \alpha)}$$ に対して、\(\large{r=\sqrt{a^2+b^2}}\)、\(\displaystyle \large{\sin \alpha = \frac{b}{r}}\)、\(\displaystyle \large{\cos \alpha = \frac{a}{r}}\) を計算します。

\(\large{r=\sqrt{1^2 + 1^2} = \sqrt{2}}\) から、 $$\large{\sin\theta +\cos \theta = \sqrt{2}\sin(\theta + \alpha)}$$ と変形されます。

ここで、\(\large{\displaystyle \sin \alpha = \frac{1}{ \sqrt{2}}}\)、\(\displaystyle \large{\cos \alpha = \frac{1}{ \sqrt{2}}}\) を満たす \(\large{\alpha}\) は、\(\displaystyle\large{\alpha = \frac{\pi}{4}}\) であるため、 $$\large{\sin\theta +\cos \theta = \sqrt{2}\sin\left(\theta + \frac{\pi}{4}\right)}$$ となります。

【別解】
三角関数の合成は、式の変形方法を覚えておけば、公式を使わなくても求めることができます。

\(\large{\sqrt{1^2 + 1^2} = \sqrt{2}}\) を \(\large{\sin \theta + \cos\theta}\) からくくり出すと、 $$\large{\sin \theta + \cos\theta = \sqrt{2}\left(\frac{1}{\sqrt{2}}\sin \theta + \frac{1}{\sqrt{2}}\cos\theta\right)}$$ ここで、\(\displaystyle\large{\sin \frac{\pi}{4} = \frac{1}{\sqrt{2}}}\)、\(\displaystyle\large{\cos \frac{\pi}{4} = \frac{1}{\sqrt{2}}}\) から、 $$\large{\sin \theta + \cos\theta = \sqrt{2}\left(\sin \theta \cos \frac{\pi}{4}+\cos\theta\sin \frac{\pi}{4}\right)}$$ \(\large{\sin}\) の加法定理から、 $$\large{\sin\theta +\cos \theta = \sqrt{2}\sin\left(\theta + \frac{\pi}{4}\right)}$$ となります。

問題(2) 三角関数の合成 | sinに変形

【解答と解説】

三角関数の合成の公式から、 $$\large{a \sin \theta + b \cos \theta = r \sin (\theta + \alpha)}$$ に対して、\(\large{r=\sqrt{a^2+b^2}}\)、\(\displaystyle \large{\sin \alpha = \frac{b}{r}}\)、\(\displaystyle \large{\cos \alpha = \frac{a}{r}}\) を計算します。

\(\large{r=\sqrt{1^2 + (\sqrt{3})^2} = 2}\) から、 $$\large{\sin\theta -\sqrt{3}\cos \theta = 2\sin(\theta + \alpha)}$$ と変形されます。

ここで、\(\large{\displaystyle \sin \alpha = \frac{-\sqrt{3}}{2}}\)、\(\displaystyle \large{\cos \alpha = \frac{1}{ 2}}\) を満たす \(\large{\alpha}\) は、\(\displaystyle\large{-\frac{\pi}{2} < \alpha < \frac{\pi}{2} }\) において \(\displaystyle\large{\alpha = -\frac{\pi}{3}}\) であるため、 $$\large{\sin\theta - \sqrt{3}\cos \theta = 2\sin\left(\theta - \frac{\pi}{3}\right)}$$ となります。

問題(3) 三角関数の合成 | sinに変形

【解答と解説】
三角関数の合成の公式から、 $$\large{a \sin \theta + b \cos \theta = r \sin (\theta + \alpha)}$$ に対して、\(\large{r=\sqrt{a^2+b^2}}\)、\(\displaystyle \large{\sin \alpha = \frac{b}{r}}\)、\(\displaystyle \large{\cos \alpha = \frac{a}{r}}\) を計算します。

\(\large{r=\sqrt{(\sqrt{2})^2 + (\sqrt{6})^2} = 2\sqrt{2}}\) から、 $$\large{\sqrt{2}\sin\theta + \sqrt{6}\cos\theta = 2\sqrt{2}\sin(\theta + \alpha)}$$ と変形されます。

ここで、\(\large{\displaystyle \sin \alpha = \frac{\sqrt{6}}{2\sqrt{2}}=\frac{\sqrt{3}}{2}}\)、\(\displaystyle \large{\cos \alpha = \frac{\sqrt{2}}{2\sqrt{2}}=\frac{1}{2}}\) を満たす \(\large{\alpha}\) は、\(\displaystyle\large{-\frac{\pi}{2} < \alpha < \frac{\pi}{2} }\) において \(\displaystyle\large{\alpha = \frac{\pi}{3}}\) であるため、 $$\large{\sqrt{2}\sin\theta + \sqrt{6}\cos\theta = 2\sqrt{2}\sin\left(\theta + \frac{\pi}{3}\right)}$$ となります。

問題(4) 三角関数の合成 | cosに変形

【解答と解説】
三角関数の合成の公式から、 $$\large{a \cos \theta + b \cos \theta = r \cos (\theta + \beta)}$$ に対して、\(\large{r=\sqrt{a^2+b^2}}\)、\(\displaystyle \large{\sin \beta = -\frac{a}{r}}\)、\(\displaystyle \large{\cos \beta = \frac{b}{r}}\) を計算します。

\(\large{r=\sqrt{(\sqrt{3})^2 + 1^2} = 2}\) から、 $$\large{\sqrt{3}\sin\theta +\cos \theta = 2\cos(\theta + \beta)}$$ と変形されます。

ここで、\(\large{\displaystyle \sin \beta = -\frac{\sqrt{3}}{ 2}}\)、\(\displaystyle \large{\cos \beta = \frac{1}{2}}\) を満たす \(\large{\beta}\) は、\(\displaystyle\large{-\frac{\pi}{2} < \alpha <\frac{\pi}{2} }\) において \(\displaystyle\large{\beta = -\frac{\pi}{3}}\) であるため、 $$\large{\sqrt{3}\sin \theta +\cos\theta = 2\cos\left(\theta - \frac{\pi}{3}\right)}$$ となります。

【別解】
\(\large{\cos}\) の三角関数の合成も、式の変形方法を覚えておけば、公式を使わなくても求めることができます。

\(\large{\sqrt{(\sqrt{3})^2 + 1^2} = 2}\) を \(\large{\sqrt{3}\sin \theta + \cos\theta}\) からくくり出すと、 $$\large{\sqrt{3}\sin \theta + \cos\theta =2\left(\frac{\sqrt{3}}{2}\sin \theta + \frac{1}{2}\cos\theta\right)}$$ ここで、\(\displaystyle\large{\sin \left(-\frac{\pi}{3}\right) = -\frac{\sqrt{3}}{2}}\)、\(\displaystyle\large{\cos \left(-\frac{\pi}{3}\right) = \frac{1}{2}}\) から、 \begin{eqnarray} & &\large 2\left(\frac{\sqrt{3}}{2}\sin \theta + \frac{1}{2}\cos\theta\right)\\[0.5em] \large &\large =&\large 2\left(\sin \theta \left(-\sin \left(-\frac{\pi}{3}\right)\right)+\cos\theta\cos \left(-\frac{\pi}{3}\right)\right)\\[0.5em] &\large =&\large 2\left(\cos\theta\cos \left(-\frac{\pi}{3}\right) - \sin \theta \sin\left(-\frac{\pi}{3}\right)\right)\\[0.5em] \end{eqnarray} \(\large{\cos}\) の加法定理から、 $$\large{\sqrt{3}\sin \theta +\cos\theta = 2\sin\left(\theta - \frac{\pi}{3}\right)}$$ となります。

【3】応用問題と解き方

三角関数の合成を利用した応用的な問題について解説します。

問題(5) は三角関数を利用して三角方程式を解く問題です。

問題(6)は 三角関数の合成を利用して三角関数の不等式を解く問題です。

問題(7)は 三角関数の合成を利用して三角関数の最大値・最小値を解く問題です。

問題(8)は 三角関数の合成を利用しますが、\(\large{\sin(\theta+\alpha)}\) の 角度\(\large{\alpha}\) が解けない場合の問題です。

問題(5) 三角関数の合成を利用する三角方程式

【解答と解説】
問題(2)の結果から、与えられた方程式の左辺は以下のように変形されます。 $$\large{\sin\theta - \sqrt{3}\cos \theta = 2\sin\left(\theta - \frac{\pi}{3}\right)}$$ したがって、問題の方程式は、 $$\large{\sin\left(\theta - \frac{\pi}{3}\right) = \frac{1}{2}}$$

\(\displaystyle\large{\theta - \frac{\pi}{3} = t}\) とおき、
$$\large{\sin t = \frac{1}{2}}$$ として方程式を解きます。

このとき、\(\large{t}\) の範囲は \(\large{0 \leqq \theta \leqq 2\pi }\) から、\(\displaystyle\large{- \frac{\pi}{3} \leqq t \leqq \frac{5}{3}\pi }\) となります。

単位円上に \(\displaystyle\large{y=\frac{1}{2}}\) の直線を描いた図を以下に示します。

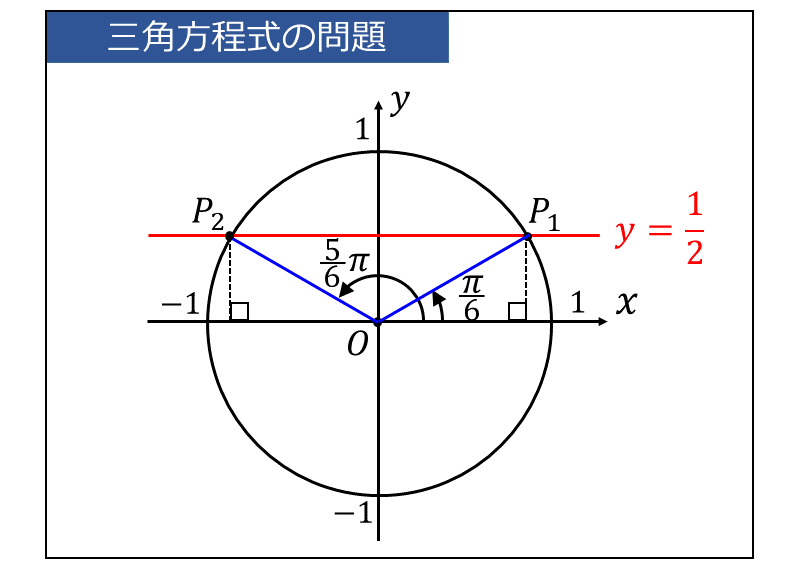
三角関数の定義から、\(\displaystyle\large{\sin t = \frac{1}{2}}\) の解は 直線 \(\displaystyle\large{y=\frac{1}{2}}\) と 単位円 の交点を点\(\large{P}\)としたときの、動径\(\large{\overline{OP}}\) の\(\large{x}\)軸の正の部分からの角度になります。

上図より、\(\displaystyle\large{\sin t = \frac{1}{2}}\) を解くと、\(\displaystyle\large{t=\frac{\pi}{6},\hspace{3pt}\frac{5}{6}\pi}\) となります。

\(\displaystyle\large{\theta - \frac{\pi}{3} = t}\) より、求める解 \(\large{\theta}\) は $$\large{\theta = \frac{\pi}{2},\hspace{3pt}\frac{7}{6}\pi}$$ となります。

問題(6) 三角関数の合成を利用する不等式

【解答と解説】
問題の三角関数に三角関数の合成を利用すると、 $$\large{\sin\theta - \cos\theta = \sqrt{2}\sin\left(\theta -\frac{\pi}{4}\right)}$$ となります。

上式から問題の不等式を変形すると、 $$\large{\sin\left(\theta -\frac{\pi}{4}\right) > \frac{1}{\sqrt{2}}}$$ となります。

ここで、\(\displaystyle\large{\theta - \frac{\pi}{4} = t}\) とおき、
$$\large{\sin t > \frac{1}{\sqrt{2}}}$$ として不等式を解きます。

このとき、\(\large{t}\) の範囲は \(\large{0 \leqq \theta < 2\pi }\) から、\(\displaystyle\large{- \frac{\pi}{4} \leqq t < \frac{7}{4}\pi }\) となります。

単位円上に \(\displaystyle\large{y=\frac{1}{\sqrt{2}}}\) の直線を描いた図を以下に示します。 \(\displaystyle\large{\sin t > \frac{1}{\sqrt{2}}}\) を満たす範囲は、上図の赤線で書かれた範囲となります。

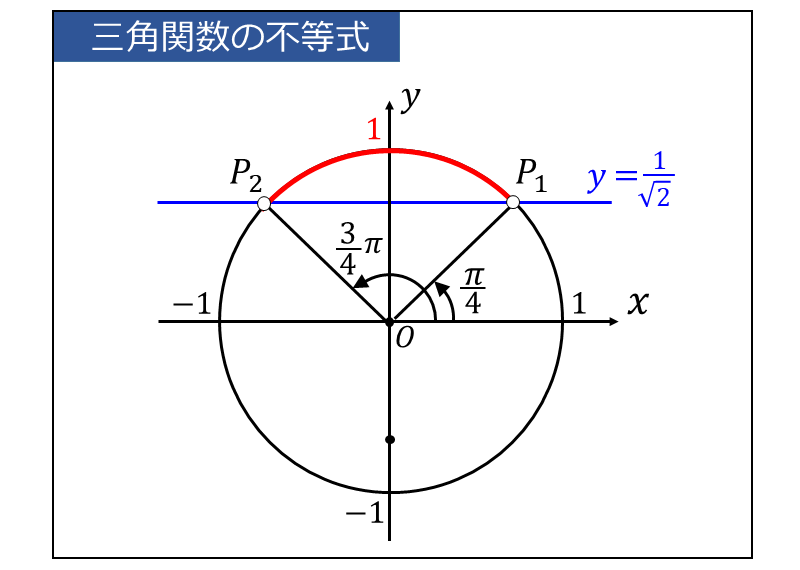
単位円と \(\displaystyle\large{y=\frac{1}{\sqrt{2}}}\) の交わる位置の動径\(\large{\overline{OP}}\) の角度は \(\displaystyle\large{\sin t = \frac{1}{\sqrt{2}}}\) を \(\displaystyle\large{- \frac{\pi}{4} \leqq t < \frac{7}{4}\pi }\) の範囲で解くことで以下のように求められます。 $$\large{t=\frac{\pi}{4}\hspace{2pt},\hspace{3pt}\frac{3}{4}\pi}$$

つまり、不等式を満たす \(\large{t}\) の範囲は $$\large{\frac{\pi}{4} < t < \frac{3}{4}\pi}$$ となります。

したがって、問題の \(\large{\theta}\) 範囲は \(\displaystyle\large{\theta - \frac{\pi}{4} = t}\) であることから、 $$\large{\frac{\pi}{4}+ \frac{\pi}{4} < t+ \frac{\pi}{4} < \frac{3}{4}\pi+ \frac{\pi}{4}}$$ $$\large{\frac{\pi}{2} < t + \frac{\pi}{4}< \pi}$$ $$\large{\frac{\pi}{2} < \theta< \pi}$$ となります。

問題(7) 三角関数の合成を利用する最大値・最小値

【解答と解説】
問題の関数は 二倍角の公式を利用して、 \(\large{\sin2\theta}\)、\(\large{\cos2\theta}\) の式に変形することができます。

二倍角の公式は、以下の式で表されます。 $$\large{\sin\theta \cos\theta = \frac{\sin 2\theta}{2}}$$ $$\large{\sin^2\theta = \frac{1-\cos2\theta}{2}}$$ $$\large{\cos^2\theta = \frac{1+\cos2\theta}{2}}$$

問題の関数を変形すると、以下のようになります。 \begin{eqnarray} \large y&\large= &\large \cos^2\theta + 2\sqrt{3}\sin\theta\cos\theta -\sin^2\theta\\[0.5em] &\large =&\large \frac{1+\cos2\theta}{2} + \sqrt{3}\sin2\theta - \frac{1-\cos2\theta}{2}\\[0.5em] &\large =&\large \sqrt{3}\sin2\theta + \cos2\theta \\[0.5em] \end{eqnarray}

ここで、三角関数の合成を適応すると、 $$\large{\sqrt{3}\sin2\theta + \cos2\theta = 2\sin\left(2\theta +\frac{\pi}{6}\right)}$$ となります。

ここで、\(\displaystyle\large{t=2\theta + \frac{\pi}{6}}\) とおくと、\(\large{t}\) の範囲は \(\displaystyle\large{0 \leqq \theta \leqq \frac{\pi}{2}}\) より $$\large{0 \leqq 2\theta \leqq \pi}$$ $$\large{\frac{\pi}{6} \leqq 2\theta + \frac{\pi}{6} \leqq \frac{7}{6}\pi}$$ $$\large{\frac{\pi}{6} \leqq t \leqq \frac{7}{6}\pi}$$ となります。

よって、\(\large{y=2\sin t}\) の最大値・最小値を \(\large{\displaystyle\frac{\pi}{6} \leqq t \leqq \frac{7}{6}\pi}\) の範囲で求めます。

ここで、単位円上に \(\displaystyle\large{\frac{\pi}{6} \leqq t \leqq \frac{7}{6}\pi}\) の範囲を青線で描いた図を以下に示します。 \(\large{\sin}\) は単位円の動径\(\large{\overline{OP}}\) の \(\large{y}\) 座標であるため、上図の青線の範囲において、\(\large{y}\) 座標が最も大きい点が \(\large{\sin t}\) の最大値、\(\large{y}\) 座標が最も小さい点が最小値となります。

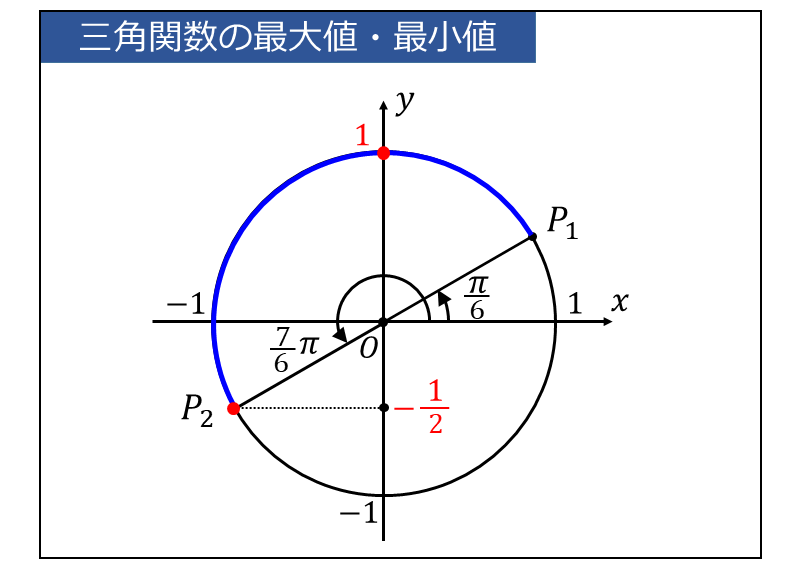
したがって、
\(\displaystyle\large{t=\frac{\pi}{2}}\) のとき 最大値 \(\displaystyle\large{2\times1 = 2}\)
\(\displaystyle\large{t=\frac{7}{6}\pi}\) のとき 最小値 \(\large{2\times\left(-\frac{1}{2}\right)=-1}\)
となります。

\(\large{t}\) を \(\large{\theta}\) に変換すると、\(\displaystyle\large{t=2\theta + \frac{\pi}{6}}\) であることから
\(\displaystyle\large{\theta=\frac{\pi}{6}}\) のとき 最大値 \(\large{2}\)
\(\displaystyle\large{\theta=\frac{\pi}{2}}\) のとき 最小値 \(\large{-1}\)
となります。

問題(8) 角度αが求められない場合の最大値・最小値

三角関数の合成の式を利用すると、問題の関数は $$\large{3\sin\theta+ \cos\theta = \sqrt{10}\sin(\theta + \alpha)}$$ であり、上式の 角度\(\large{\alpha}\) は $$\large{\sin \alpha = \frac{1}{\sqrt{10}}}$$ $$\large{\cos \alpha = \frac{3}{\sqrt{10}}}$$ を満たします。

上式の \(\large{\alpha}\) を \(\large{x}\)軸の正の部分から反時計回りに計った角度とすると、以下の図のようになります。

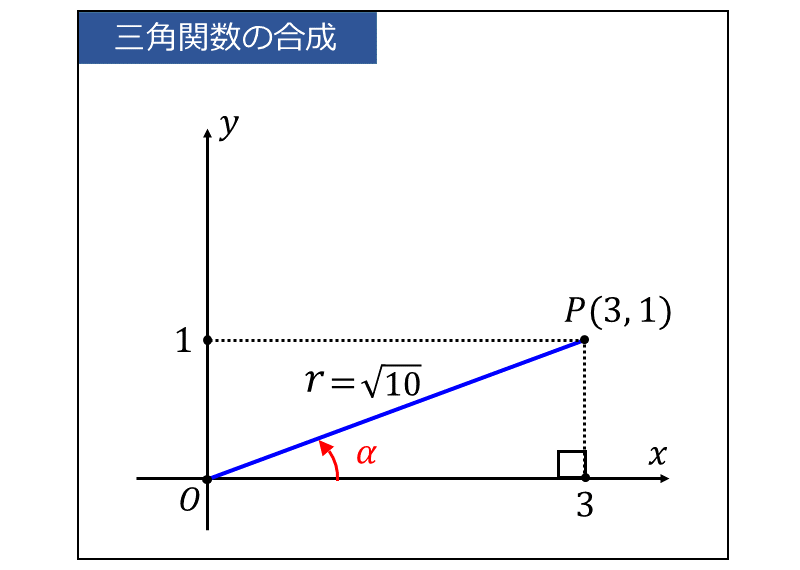
上図から、角度\(\large{\alpha}\) は \(\displaystyle\large{0 < \alpha < \frac{\pi}{4}}\) を満たすことが分かります。

ここで、\(\displaystyle\large{0 \leqq \theta \leqq \frac{\pi}{2}}\) であるから、角度\(\large{\theta+\alpha}\) の範囲は、 $$\large{\alpha \leqq \theta+\alpha \leqq \frac{\pi}{2}+\alpha}$$ となります。

上記の式の \(\displaystyle\large{\frac{\pi}{2}+\alpha}\) の範囲を求めます。 \(\displaystyle\large{0 < \alpha < \frac{\pi}{4}}\) であるから、 $$\large{0 < \alpha < \frac{\pi}{4}}$$ $$\large{\frac{\pi}{2} < \frac{\pi}{2}+\alpha < \frac{\pi}{2}+\frac{\pi}{4}}$$ $$\large{\frac{\pi}{2} < \frac{\pi}{2}+\alpha < \frac{3}{4}\pi}$$ となります。

上式から、\(\large{\theta + \alpha}\) の範囲を単位円上に青線で描くと以下のようになります。

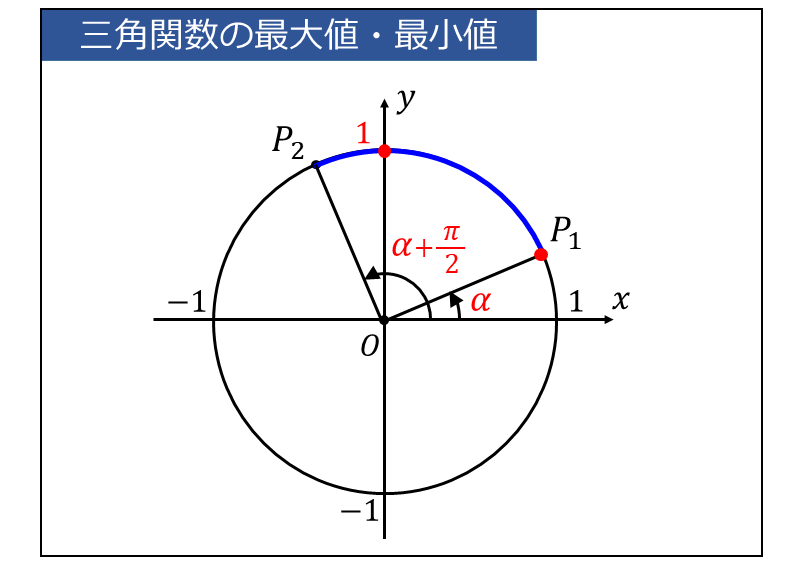
上図から、\(\large{\sin(\theta + \alpha)}\) は
\(\displaystyle\large{\theta + \alpha = \frac{\pi}{2} }\) すなわち \(\displaystyle\large{\theta = \frac{\pi}{2}-\alpha}\) のとき、最大値 \(\large{1}\)
\(\displaystyle\large{\theta + \alpha = \alpha }\) すなわち \(\displaystyle\large{\theta = 0}\) のとき、最小値 \(\displaystyle\large{\sin\alpha = \frac{1}{\sqrt{10}}}\)
をとります。

したがって、\(\large{y= 3\sin\theta+ \cos\theta = \sqrt{10}\sin(\theta + \alpha)}\) は
\(\displaystyle\large{\theta = \frac{\pi}{2}-\alpha}\) のとき最大値 \(\large{\sqrt{10}\times1=\sqrt{10}}\)
\(\displaystyle\large{\theta = 0}\) のとき、 最小値 \(\displaystyle\large{\sqrt{10}\times\frac{1}{\sqrt{10}} = 1}\)
となります。(ただし、\(\large{\alpha}\)は \(\displaystyle\large{\sin \alpha = \frac{1}{\sqrt{10}}}\)、 \(\displaystyle\large{\cos \alpha = \frac{3}{\sqrt{10}}}\) を満たす)

---