三角方程式
本項では以下の内容を解説しています。
- ・三角方程式の解法
- ・三角方程式を解くときの図の書き方
- ・関連する問題
【1】三角方程式の解き方
三角方程式とは、 $$\displaystyle \large{2 \sin \theta = \sqrt{3},\hspace{3pt}\sqrt{2}\cos \theta =1}$$ など、式中に三角関数を含んだ方程式のことをいいます。
本章では、三角方程式の解法について解説します。
【1-1】三角方程式の解法 | 変形のパターン
まず、三角方程式を解くときは、 $$\large{\sin \theta = \frac{\sqrt{3}}{2},\hspace{2pt}\cos \theta = \frac{1}{\sqrt{2}}}$$ のように "三角関数" と "定数" が等号で結ばれる式に変形します。
このとき、三角方程式を変形する方法に、いくつかのパターンが存在します。
例. \(\large{ \sin^2 \theta -\sin \theta = 0}\)
2. 相互関係の式, 二倍角の公式で変換
例. \(\large{ \cos^2 \theta + \sin\theta+1 = 0}\)
\(\large{ \cos \theta = \cos 2 \theta}\)
3. 三角関数の合成を利用する
例. \(\large{\sqrt{3}\sin\theta +\cos \theta = \sqrt{2}}\)
上記のそれぞれの詳しい解法については、後述する【3】三角方程式の応用問題で詳しく解説します。
【1-2】三角方程式の解法 | 図の書き方
三角方程式は、 "三角関数" と "定数\(\large{A}\)" が等号で結ばれた \(\large{\sin \theta = A}\) の式を解くときに、式を満たす 角度\(\large{\theta}\) を図に書くことで、角度\(\large{\theta}\)の定義域 や 解の符号 を分かりやすく求めることができます。
以下に、\(\large{\sin}\)、\(\large{\cos}\)、\(\large{\tan}\) のそれぞれの場合の図の書き方について解説します。
・sinθ=A の解法
三角関数の定義から、『\(\large{\sin \theta}\) とは 角度\(\large{\theta\hspace{2pt}}\)をもつ動径\(\large{\hspace{2pt}\overline{OP}\hspace{2pt}}\)の\(\large{\hspace{2pt} y\hspace{2pt} }\)座標』を表します。
そこで、単位円に \(\displaystyle \large{\color{red}{y=A}}\) の直線を書くことで、\(\large{\sin \theta = A}\) を満たす動径\(\large{\hspace{2pt}\color{blue}{\overline{OP}}\hspace{2pt}}\)を図示します。
このとき、\(\large{\theta}\) の定義域が \(\large{0 \leqq \theta < 2\pi }\) であれば、下図の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}\hspace{2pt}}\)の角度\(\large{\hspace{2pt}\theta_1,\hspace{2pt}\theta_2}\) が求める解となります。
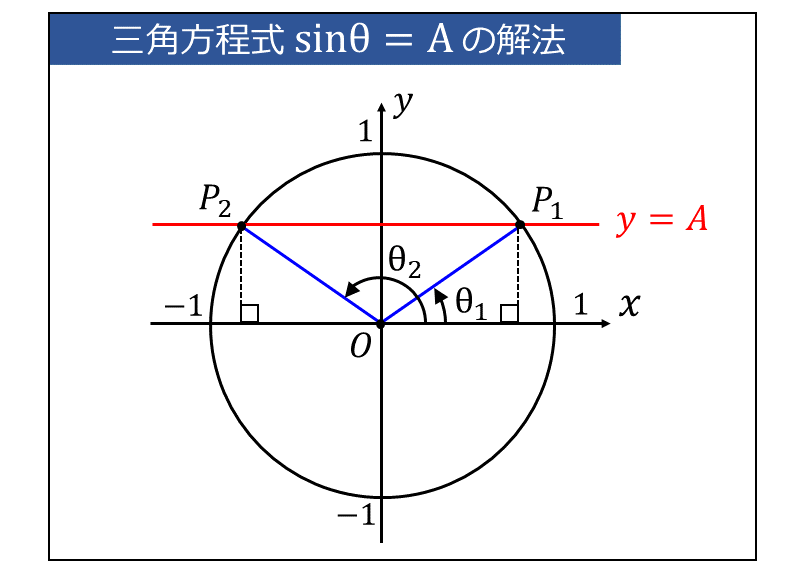
また、\(\large{\sin \theta}\) は \(\large{2\pi}\) を周期にもつ関数です。整数を \(\large{n}\) とすると、\(\large{\theta = 2n\pi}\) ごとに同じ値をとります。
したがって、\(\large{\theta}\) の範囲に制限がない場合の一般解は以下のようになります。
$$\large{\theta = \theta_1+ 2n\pi, \hspace{2pt}\theta_2+2n\pi}$$
(三角関数の周期については別ページに解説しています。)
・cosθ=A の解法
三角関数の定義から、『\(\large{\cos \theta}\) とは 角度\(\large{\theta\hspace{2pt}}\)をもつ動径\(\large{\hspace{2pt}\overline{OP}\hspace{2pt}}\)の\(\large{\hspace{2pt} x\hspace{2pt} }\)座標』を表します。
そこで、単位円に \(\displaystyle \large{\color{red}{x=A}}\) の直線を書くことで、\(\large{\cos \theta = A}\) を満たす動径\(\large{\hspace{2pt}\color{blue}{\overline{OP}}\hspace{2pt}}\)を図示します。
このとき、\(\large{\theta}\) の定義域が \(\large{0 \leqq \theta < 2\pi }\) であれば、下図の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}\hspace{2pt}}\)の角度\(\large{\hspace{2pt}\theta_1,\hspace{2pt}\theta_2}\) が求める解となります。
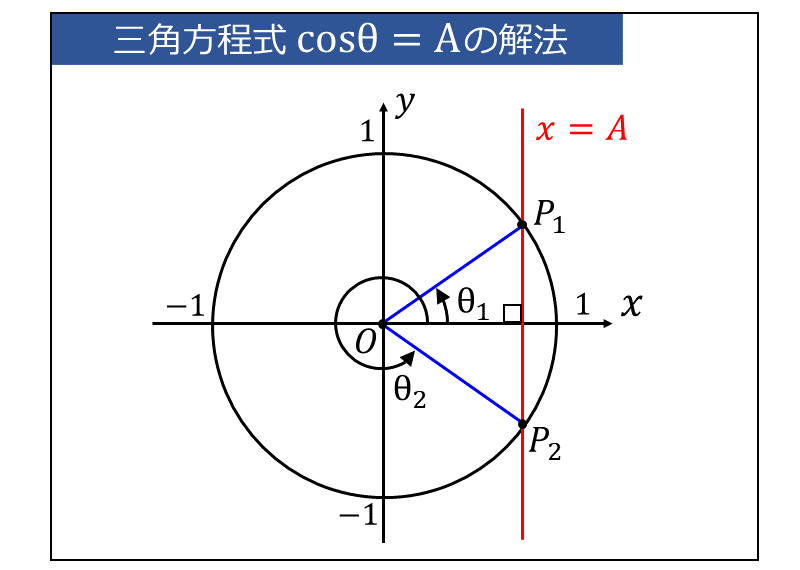
\(\large{\cos \theta}\) は \(\large{2\pi}\) を周期にもつ関数です。整数を \(\large{n}\) とすると、\(\large{\theta = 2n\pi}\) ごとに同じ値をとります。
したがって、\(\large{\theta}\) の範囲に制限がない場合の一般解は以下のようになります。
$$\large{\theta = \theta_1+ 2n\pi, \hspace{2pt}\theta_2+2n\pi}$$
・tanθ=A の解法
三角関数の定義から、『\(\large{\tan \theta}\) は 単位円の動径を延長した線と \(\large{x=1}\) の直線の交点の\(\large{\hspace{2pt}y\hspace{2pt}}\)座標』を表します。
そこで、単位円に \(\displaystyle \large{\color{green}{x=1}}\) の直線を引き、座標 \(\large{\color{red}{(1,A)}}\) を通る動径\(\large{\overline{OP}}\)を図示します。
このとき、\(\large{\theta}\) の定義域が \(\large{0 \leqq \theta < 2\pi }\) であれば、下図の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}\hspace{2pt}}\)の角度\(\large{\hspace{2pt}\theta_1,\hspace{2pt}\theta_2}\) が求める解となります。
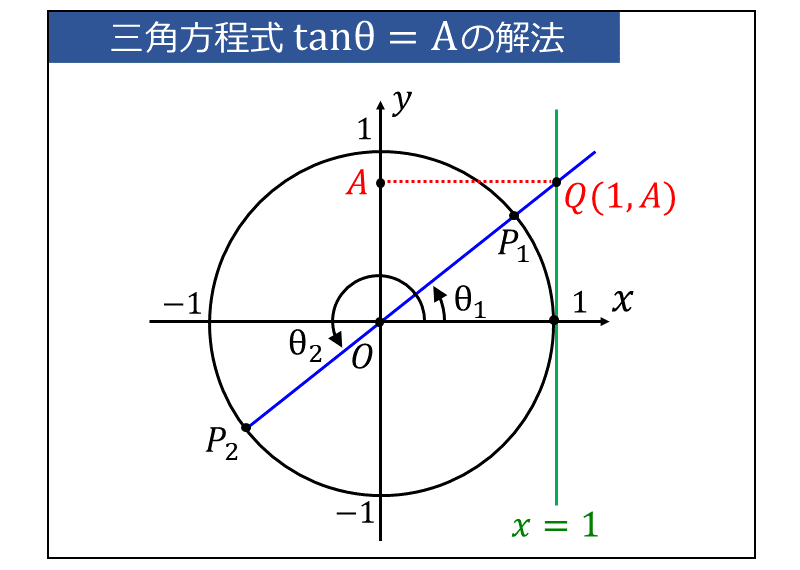
\(\large{\tan \theta}\) は \(\large{\pi}\) を周期にもつ関数です。整数を \(\large{n}\) とすると、\(\large{\theta = n\pi}\) ごとに同じ値をとります。
したがって、\(\large{\theta}\) の範囲に制限がない場合の一般解は以下のようになります。
$$\large{\theta = \theta_1+ n\pi}$$
(上図からも分かるように、\(\large{\theta_1 + \pi = \theta_2}\) の関係があるため、一般解は1つの式で表されます。)
【2】三角方程式の基本的な問題
本章では、以下の三角方程式の基本的な問題について解説します。
問題1. sinθの問題
以下の三角方程式について考えます。
\(\displaystyle \large{2\sin \theta = 1}\)
また、\(\large{\theta}\) の範囲に制限がないときの一般解を求めよ。
【解答と解説】
まず、与えられた問題の方程式を
$$\displaystyle \large{\sin \theta = \frac{1}{2}}$$
の形に変形します。
ここで、単位円に \(\displaystyle \large{y=\frac{1}{2}}\) の直線を書いた図を示します。
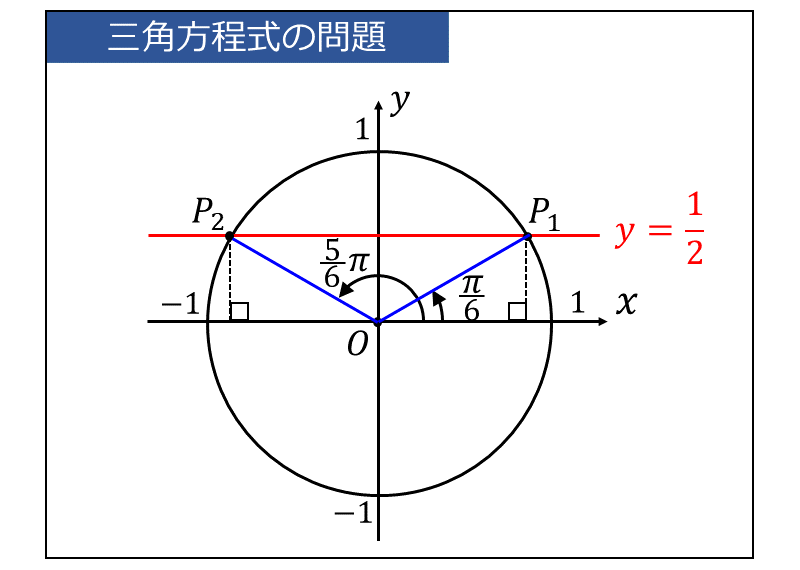
求める解\(\large{\theta}\) は、上図の動径 \(\large{\overline{OP_1}}\) と \(\large{\overline{OP_2}}\) のなす角度となります。
したがって、\(\large{0 \leqq \theta < 2\pi }\) の範囲において、 $$\displaystyle \large{\theta = \frac{1}{6}\pi,\hspace{2pt} \frac{5}{6}\pi}$$ が求める解となります。
また、\(\large{\theta}\) の範囲に制限がない場合の一般解は、整数を \(\large{n}\) とすると、 $$\large{\theta = \frac{1}{6}\pi + 2n\pi, \hspace{2pt}\frac{5}{6}\pi+2n\pi}$$ となります。
問題2. cosθの問題
以下の三角方程式について考えます。
\(\displaystyle \large{\sqrt{2}\cos \theta = -1}\)
また、\(\large{\theta}\) の範囲に制限がないときの一般解を求めよ。
【解答と解説】
まず、与えられた方程式を変形すると
$$\displaystyle \large{\cos \theta = -\frac{1}{\sqrt{2}}}$$
となります。
ここで、単位円に \(\displaystyle \large{x=-\frac{1}{\sqrt{2}}}\) の直線を書いた図を示します。
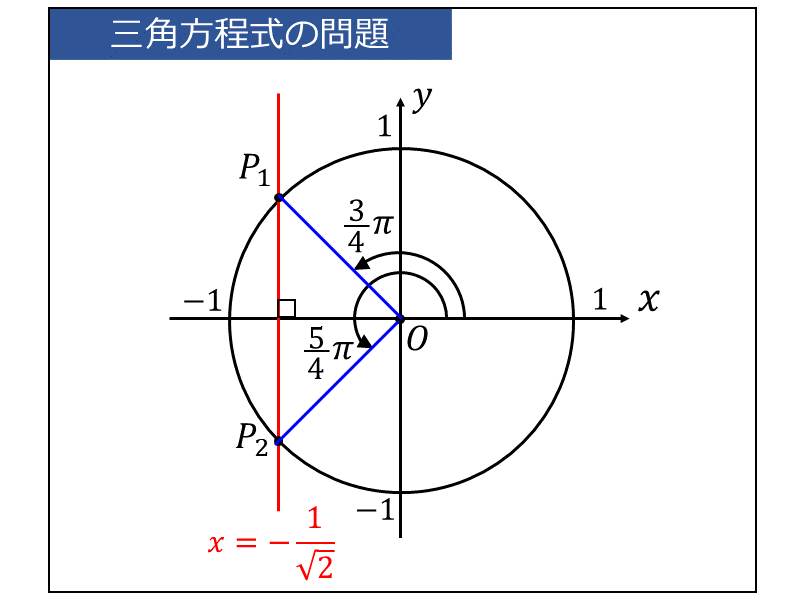
求める解\(\large{\theta}\) は、上図の動径 \(\large{\overline{OP_1}}\) と \(\large{\overline{OP_2}}\) のなす角度となります。
したがって、\(\large{0 \leqq \theta < 2\pi }\) の範囲において、 $$\displaystyle \large{\theta = \frac{3}{4}\pi,\hspace{2pt} \frac{5}{4}\pi}$$ が求める解となります。
また、\(\large{\theta}\) の範囲に制限がない場合の一般解は、整数を \(\large{n}\) とすると、 $$\large{\theta = \frac{3}{4}\pi + 2n\pi, \hspace{2pt}\frac{5}{4}\pi+2n\pi}$$ となります。
問題3. tanθの問題
以下の三角方程式について考えます。
\(\displaystyle \large{-\tan \theta = \sqrt{3}}\)
また、\(\large{\theta}\) の範囲に制限がないときの一般解を求めよ。
【解答と解説】
まず、与えられた方程式を変形すると
$$\displaystyle \large{\tan \theta = -\sqrt{3}}$$
となります。
ここで、単位円の動径を延長し、\(\displaystyle \large{x=1}\) の直線との交点が\(-\large{\sqrt{3}}\) となるときの図を示します。
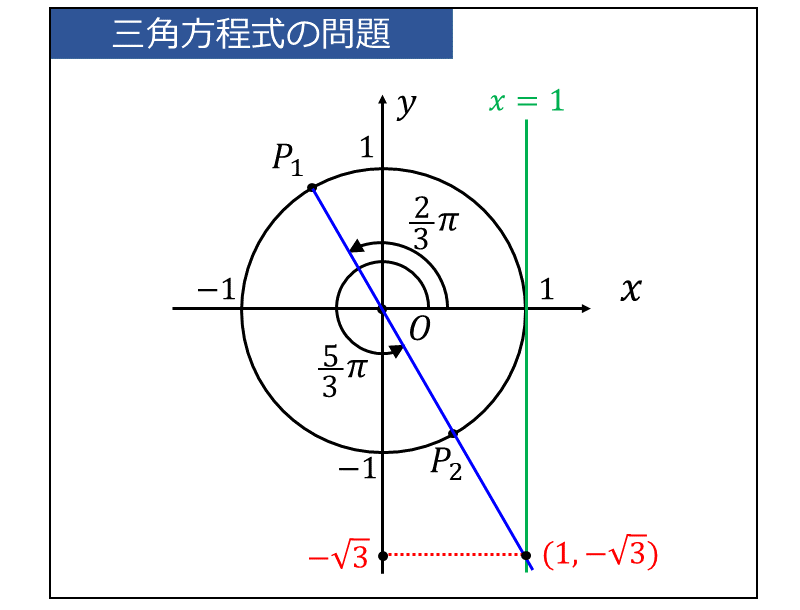
求める解\(\large{\theta}\) は、上図の動径 \(\large{\overline{OP_1}}\) と \(\large{\overline{OP_2}}\) のなす角度となります。
したがって、\(\large{0 \leqq \theta < 2\pi }\) の範囲において、 $$\displaystyle \large{\theta = \frac{2}{3}\pi,\hspace{2pt} \frac{5}{3}\pi}$$ が求める解となります。
また、\(\large{\theta}\) の範囲に制限がない場合の一般解は、整数を \(\large{n}\) とすると、 $$\large{\theta = \frac{2}{3}\pi + n\pi}$$ となります。
【3】三角方程式の応用問題
本章では、以下の三角方程式の応用的な問題について解説します。
三角方程式の解法には、いくつかのパターンが存在します。
2. 相互関係の式 や 二倍角の公式で変換
3. 三角関数の合成を利用する
問題(4), (5), (6)は \(\large{\sin \theta = t}\) など置き換えを利用する問題です。
問題(7), (8)は 三角関数の相互関係 や 二倍角の公式 を利用し変換する問題です。
問題4. 置き換えを利用する三角方程式
以下の三角方程式について考えます。
\(\displaystyle \large{2\sin^2 \theta -3\sin \theta =-1}\)
【解答と解説】
問題の方程式は
$$\large{\sin \theta = A}$$
の式に変形することができないため、置換を利用して解を求めます。
\(\large{\sin \theta = t}\) とおくと、与えられた方程式は $$\large{2t^2 -3t +1 =0}$$ と \(\large{t}\) に関する二次方程式になります。
ここで、\(\large{0 \leqq \theta < 2\pi }\) のとき、\(\large{t}\)の範囲は \(\large{-1 \leqq t \leqq 1}\) となります。
\(\large{2t^2 -3t +1 =0}\) を変形すると、 $$\large{(t-1)(2t-1)=0}$$ となるため、\(\large{t}\) に関する方程式の解は $$\displaystyle \large{t= 1,\hspace{2pt}\frac{1}{2}}$$ となります。
\(\large{\sin \theta = 1}\) の解は $$\displaystyle \large{\theta = \frac{1}{2}\pi}$$ となります。
また、\(\displaystyle \large{\sin \theta = \frac{1}{2}}\) の解は $$\displaystyle \large{\theta = \frac{1}{6}\pi,\hspace{2pt}\frac{5}{6}\pi}$$ となります。
よって、求める解は、 $$\large{\theta = \frac{1}{2}\pi,\hspace{2pt}\frac{1}{6}\pi,\hspace{2pt}\frac{5}{6}\pi}$$ となります。
問題5. 置き換えを利用する三角方程式
以下の三角方程式について考えます。
\(\displaystyle \large{\sin 2\theta =-\frac{1}{\sqrt{2}}}\)
【解答と解説】
問題の方程式は 三角関数に \(\large{2\theta}\) が含まれています。このような問題では、置換を利用することで解きやすくなります。
$$\large{2 \theta = t}$$
とおくと、\(\large{\theta}\) の定義域は \(\large{0 \leqq \theta < 2\pi }\) であるため、\(\large{t}\) の範囲は \(\large{0 \leqq t < 4\pi}\) となります。
\(\large{2\theta =t}\) とおいた問題の方程式は $$\large{\sin t =-\frac{1}{\sqrt{2}}}$$ となります。
ここで、単位円に直線 \(\displaystyle \large{y=-\frac{1}{\sqrt{2}}}\) を書き、\(\displaystyle \large{\sin t =-\frac{1}{\sqrt{2}}}\) を満たす \(\large{t_1,\hspace{2pt}t_2}\) を表した図を示します。
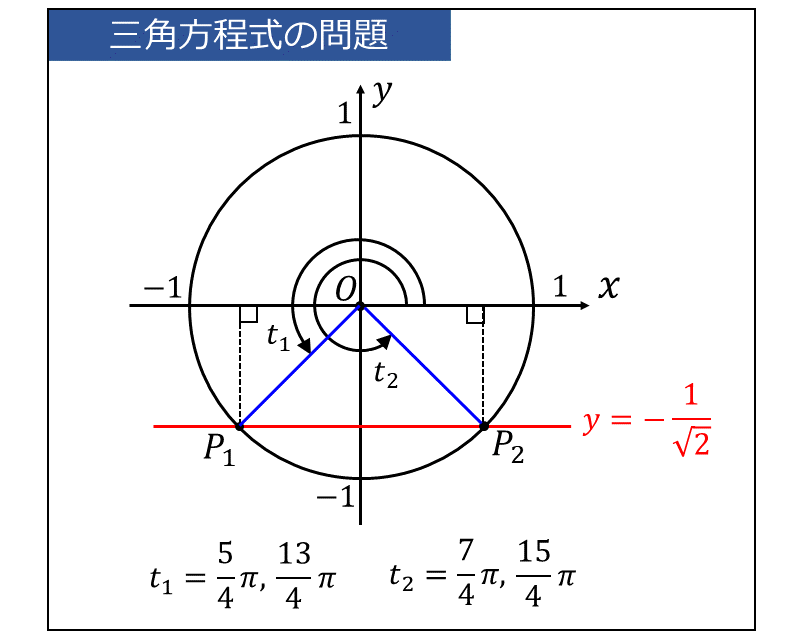
ここで、\(\large{t}\) の定義域が \(\large{0 \leqq t < 4\pi}\) であることに注意が必要です。単位円の一周が \(\large{2\pi}\) であるため、 \(\large{t}\) は単位円を二周する範囲から解を求めます。
\(\large{t}\) について解くと、 $$\large{t= \frac{5}{4}\pi,\hspace{2pt}\frac{7}{4}\pi,\hspace{2pt}\frac{13}{4}\pi,\hspace{2pt}\frac{15}{4}\pi}$$ となります。
したがって、\(\large{2\theta = t}\) から、求める解 \(\large{\theta}\) は、 $$\large{\theta = \frac{5}{8}\pi,\hspace{2pt}\frac{7}{8}\pi,\hspace{2pt}\frac{13}{8}\pi,\hspace{2pt}\frac{15}{8}\pi}$$ となります。
問題6. 置き換えを利用する三角方程式
以下の三角方程式について考えます。
\(\displaystyle \large{\cos \left(\theta-\frac{1}{2}\pi \right) =\frac{1}{2}}\)
【解答と解説】
問題の方程式は 三角関数に \(\large{\theta-\frac{1}{2}\pi}\) が含まれています。この問題も、置換を利用することで解きやすくなります。
$$\large{\theta-\frac{1}{2}\pi = t}$$
とおくと、\(\large{\theta-\frac{1}{2}\pi}\) の範囲は
$$\large{-\frac{1}{2}\pi \leqq \theta-\frac{1}{2}\pi < \frac{3}{2}\pi}$$
より
$$\large{-\frac{1}{2}\pi \leqq t < \frac{3}{2}\pi}$$
となります。
したがって、この範囲における \(\large{\cos t=\frac{1}{2}}\) の解は、 $$\large{t=-\frac{1}{3}\pi,\hspace{2pt}\frac{1}{3}\pi}$$ となります。
つまり、\(\large{\theta-\frac{1}{2}\pi = t}\) より、求める解\(\large{\theta}\)は、 $$\large{\theta = \frac{1}{6}\pi,\hspace{2pt}\frac{5}{6}\pi}$$ となります。
【別解】
上記の問題は、sinとcosの関係を利用すると、簡単に解くことができます。
\(\large{\sin \theta}\) は \(\large{\cos \theta}\) を \(\large{\theta}\)軸方向に\(\large{+\frac{1}{2}\pi}\)だけ平行移動した関数であるため、以下が成り立ちます。 $$\large{\cos (\theta-\frac{1}{2}\pi) = \sin \theta}$$ したがって、問題の三角方程式は、 $$\large{\sin \theta =\frac{1}{2}}$$ となります。 したがって、求める解\(\large{\theta}\)は、 $$\large{\theta =\frac{1}{6}\pi,\hspace{2pt}\frac{5}{6}\pi}$$
この解き方の場合、\(\large{\sin \theta = A}\) の式に直接変形できるため、置換するよりも簡単に解くことができます。
問題7. 三角関数の変換 | 相互関係を利用
\(\displaystyle \large{\cos^2 \theta + \sin\theta = -1}\)
【解答と解説】
問題の方程式は \(\large{\sin}\) と \(\large{\cos}\) がどちらも含まれています。このような問題では、相互関係の式を利用して、 \(\large{\sin}\) か \(\large{\cos}\) のどちらか一方にそろえて解きます。
三角関数の相互関係の式から、 $$\large{\sin^2 \theta + \cos^2 \theta = 1 }$$ が成り立ちます。
問題の三角方程式を変形すると、 $$\large{(1-\sin^2 \theta) + \sin \theta = -1}$$ $$\large{-\sin^2 \theta + \sin \theta +2= 0}$$
\(\large{\sin \theta = t}\) とおくと、与えられた方程式は
$$\large{t^2 -t -2=0}$$
と \(\large{t}\) に関する二次方程式になります。
ここで、\(\large{0 \leqq \theta < 2\pi }\) のとき、\(\large{t}\)の範囲は \(\large{-1 \leqq t \leqq 1}\) となります。
\(\large{t^2 -t -2 =0}\) を変形すると、 $$\large{(t-2)(t+1) = 0}$$ となります。 \(\large{-1 \leqq t \leqq 1}\) を満たす解は $$\large{t=-1}$$ であり、\(\large{\sin \theta = -1}\)を解くと、求める解\(\large{\theta}\) は $$\large{\theta = \frac{3}{2}\pi}$$ となります。
問題8. 三角関数の変換 | 二倍角の公式
\(\displaystyle \large{\cos \theta = \cos 2 \theta}\)
【解答と解説】
問題の方程式は \(\large{\cos 2 \theta}\) が含まれているため、三角関数の二倍角の公式により変換して解きます。
二倍角の公式は、 $$\large{\cos 2 \theta = 2 \cos^2\theta -1}$$ であるため、問題の方程式を変形すると $$\large{\cos \theta = 2 \cos^2 \theta -1}$$ $$\large{2 \cos^2 -\cos \theta -1 = 0}$$ となります。
\(\large{\cos \theta = t}\) とおくと、\(\large{t}\) の範囲は \(\large{-1 \leqq t \leqq 1 }\) となります。
問題の二次方程式を変形すると、 $$\large{2t^2 -t -1 = 0}$$ $$\large{(2t+1)(t-1)=0}$$ となります。
よって、\(\large{t=1,\hspace{2pt}-\frac{1}{2}}\) が \(\large{t}\) の方程式の解となります。
したがって、求める解\(\large{\theta}\)は、 $$\large{\theta = 0,\hspace{2pt}\frac{2}{3}\pi,\hspace{2pt}\frac{4}{3}\pi}$$ となります。
【別解】
問題の三角方程式は、\(\large{\cos \theta}\) と \(\large{\cos 2\theta}\) の関係を式で表すことで、二倍角の公式を使わずに解くことができます。
下図より、\(\large{\cos \theta}\) と \(\large{\cos 2\theta}\) が一致することは、角度\(\large{\theta}\) と 角度\(\large{2\theta}\) の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}}\) の\(\large{x}\)座標が一致することを意味します。
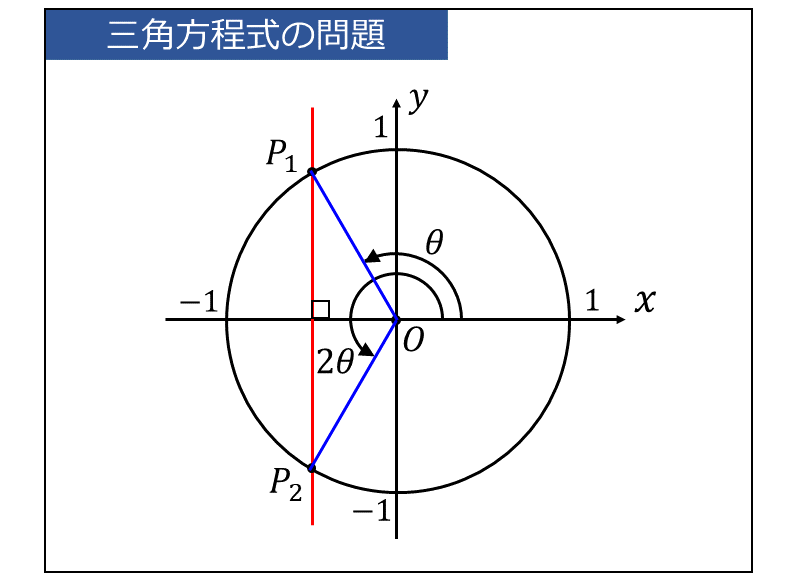
角度\(\large{\theta}\) と 角度\(\large{2\theta}\) の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}}\) の\(\large{x}\)座標が一致する条件は、以下の2つの場合です。
・条件① : 『\(\large{\theta}\) と \(\large{2\theta}\) の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}}\) が一致』 すなわち、 $$\large{2\theta = \theta + 2n\pi}$$ ・条件② : 『\(\large{\theta}\) と \(\large{2\theta}\) の動径\(\large{\hspace{2pt}\overline{OP_1},\hspace{2pt}\overline{OP_2}}\) が\(\large{x}\)軸対称』 すなわち、 $$\large{2\theta = -\theta + 2n\pi}$$ ただし、\(\large{n}\)を整数とする
条件①から $$\large{\theta = 2n\pi}$$ 条件②から $$\large{\theta = \frac{2}{3}n\pi}$$ が導かれます。
よって、上記の条件から \(\large{0 \leqq \theta < 2\pi }\) の解を求めると、 $$\large{\theta = 0,\hspace{2pt}\frac{2}{3}\pi,\hspace{2pt}\frac{4}{3}\pi}$$ と求められます。
問題9. 三角関数の合成を利用する
\(\displaystyle \large{\sqrt{3}\sin\theta +\cos \theta = \sqrt{2}}\)
【解答と解説】
問題の方程式は 三角関数の合成を利用して解きます。
三角関数の合成は、 $$\large{a \sin \theta + b \cos \theta = r \sin (\theta + \alpha)}$$ に対して、\(\large{r=\sqrt{a^2+b^2}}\)、\(\displaystyle \large{\sin \alpha = \frac{b}{\sqrt{a^2+b^2}}}\)、\(\displaystyle \large{\cos \alpha = \frac{a}{\sqrt{a^2+b^2}}}\) を利用して求めます。
与えられた三角方程式の左辺に、三角関数の合成を利用すると、 $$\large{\sqrt{3}\sin\theta +\cos \theta = 2\sin(\theta + \alpha)}$$ ここで、\(\large{\displaystyle \sin \alpha = \frac{1}{2}}\)、\(\displaystyle \large{\cos \alpha = \frac{\sqrt{3}}{2}}\) であるため、 $$\large{\sqrt{3}\sin\theta +\cos \theta = 2\sin(\theta + \frac{1}{6}\pi)}$$ となります。
与えられた三角方程式は、 $$\large{2\sin(\theta + \frac{1}{6}\pi) = \sqrt{2}}$$ $$\large{\sin(\theta + \frac{1}{6}\pi) = \frac{\sqrt{2}}{2}}$$ と変形されます。ここで、 $$\large{\theta+\frac{1}{6}\pi = t}$$ とおくと、\(\large{\theta}\) の定義域は $$\large{\frac{1}{6}\pi \leqq \theta+\frac{1}{6}\pi < \frac{13}{6}\pi}$$ より $$\large{\frac{1}{6}\pi \leqq t < \frac{13}{6}\pi}$$ となります。
したがって、この範囲における \(\displaystyle \large{\sin t=\frac{\sqrt{2}}{2}}\) の解は、 $$\large{t=\frac{1}{4}\pi,\hspace{2pt}\frac{3}{4}\pi}$$ となります。
つまり、求める解\(\large{\theta}\)は、 $$\large{\theta = \frac{1}{12}\pi,\hspace{2pt}\frac{7}{12}\pi}$$ となります。