三角関数の加法定理

本項では、まず 三角関数の加法定理 の公式と証明について解説します。

次に、加法定理の基礎的な問題 と 応用問題 について解説します。

【1】加法定理の証明

加法定理とは、角度\(\large{\alpha}\)、\(\large{\beta}\) の和と差の三角関数を求める公式です。

本章では、三角関数の加法定理を証明する方法について解説します。

【1-1】2点間の距離の公式による証明

まず以下の \(\large{\cos(\alpha -\beta)}\) の式を証明します。 $$\large{\cos(\alpha +\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta}$$

\(\large{\cos(\alpha +\beta)}\) の式を証明することができれば、他の加法定理の公式も導くことができます。

まず、以下の図のように単位円の 動径\(\large{\overline{OP}}\) の角度が \(\large{\alpha + \beta}\) であるとします。

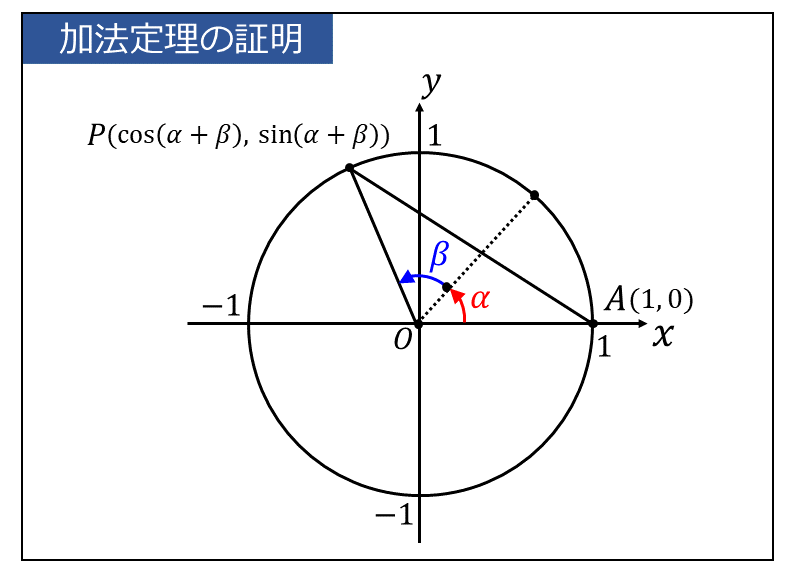
このとき、点\(\large{P}\)の座標は、 $$\large{P\hspace{2pt}(\hspace{2pt}\cos(\alpha + \beta)\hspace{2pt},\hspace{2pt}\sin(\alpha + \beta)\hspace{2pt})}$$ となります。

ここで、図中の点\(\large{A(1,0)}\) と点\(\large{P}\) の距離\(\large{\overline{AP}}\)を求めると、2点間の距離の公式から \begin{eqnarray} \large \overline{AP}^2&\large =&\large \{\cos(\alpha + \beta)-1\}^2 + \{\sin(\alpha + \beta)-0\}^2 \\[0.4em] \large &\large =&\large \cos^2(\alpha + \beta)-2\cos(\alpha + \beta) +1+ \sin^2(\alpha + \beta) \\[0.4em] \end{eqnarray} 三角関数の相互関係から、\(\large{\sin^2(\alpha + \beta) + \cos^2(\alpha + \beta) = 1}\) より、 $$\large{\overline{AP}^2 = 2-2\cos(\alpha + \beta)}$$ となります。

次に、以下の図のように単位円の動径\(\large{\overline{OP}}\) の角度を \(\large{-\alpha}\) だけ回転させた場合について考えます。

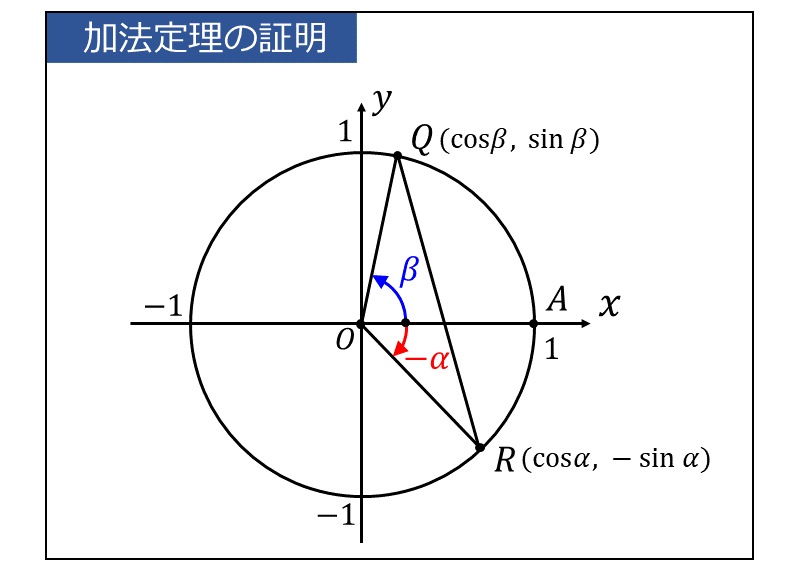
このとき、図中の点\(\large{Q}\)、点\(\large{R}\)の座標は以下のようになります。 $$\large{Q\hspace{2pt}(\cos \beta,\sin \beta)}$$ $$\large{R\hspace{2pt}(\cos \alpha,-\sin \alpha)}$$ ここで、点\(\large{Q}\) と点\(\large{R}\) の距離\(\large{\overline{QR}}\) を2点間の公式から求めると、 \begin{eqnarray} \large \overline{QR}^2&\large =&\large (\cos\beta - \cos\alpha)^2 + (\sin\beta + \sin\alpha)^2 \\[0.4em] \large &\large =&\large 2-2(\cos \alpha \cos\beta - \sin \alpha \sin \beta) \\ \end{eqnarray}

このとき、 $$\large{\overline{AP} = \overline{QR}}$$ であるため、 $$\large{2-2\cos(\alpha + \beta)= 2-2(\cos \alpha \cos\beta - \sin \alpha \sin \beta)}$$ したがって、 $$\large{\cos(\alpha +\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta\hspace{10pt}(1)}$$ が導かれます。

・cos(α-β)の公式

(1)式に三角関数の性質を適応して他の加法定理を導くことができます。
まず、\(\large{\cos(\alpha +\beta)}\) から \(\large{\cos(\alpha -\beta)}\) の公式を導きます。

\(\large{\cos(-\beta) = \cos \beta}\), \(\large{\sin( -\beta)=-\sin\beta}\) であるため、(1)式の角度\(\large{\beta}\) を \(\large{-\beta}\) に置き換えると、 \begin{eqnarray} \large \cos(\alpha -\beta)&\large =&\large \cos \alpha \cos (-\beta) - \sin \alpha \sin (-\beta) \\[0.5em] \large &\large =&\large \cos \alpha \cos \beta + \sin \alpha \sin \beta\hspace{10pt}(2) \\ \end{eqnarray} が導かれます。

・sin(α+β)の公式

次に、\(\large{\cos(\alpha -\beta)}\) から \(\large{\sin(\alpha +\beta)}\) の公式を導きます。

90°-θの公式 \(\displaystyle\large{\sin \theta = \cos\left(\frac{\pi}{2}-\theta\right)}\) を利用すると \begin{eqnarray} \large \sin(\alpha +\beta)&\large =&\large \cos \left(\frac{\pi}{2}-(\alpha+\beta)\right) \\[0.4em] &\large =&\large \cos \left((\frac{\pi}{2}-\alpha)-\beta\right) \\[0.4em] &\large =&\large \cos \left(\frac{\pi}{2}-\alpha\right) \cos \beta + \sin \left(\frac{\pi}{2}-\alpha\right) \sin \beta \\[0.4em] &\large =&\large \sin \alpha \cos \beta + \cos \alpha \sin \beta\hspace{10pt}(3) \\ \end{eqnarray} が導かれます。

・sin(α-β)の公式

次に、\(\large{\sin(\alpha +\beta)}\) から \(\large{\sin(\alpha -\beta)}\) の公式を導きます。

(3)式の角度\(\large{\beta}\) を \(\large{-\beta}\) に置き換えると、三角関数の性質から \(\large{\cos(-\beta) = \cos \beta}\), \(\large{\sin( -\beta)=-\sin\beta}\) であるため、 \begin{eqnarray} \large \sin(\alpha -\beta)&\large =&\large \sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta) \\[0.4em] \large &\large =&\large \sin \alpha \cos \beta - \cos \alpha \sin \beta\hspace{10pt}(4) \\ \end{eqnarray} が導かれます。

・tan(α+β)の公式

次に、\(\large{\tan(\alpha +\beta)}\) の公式を導きます

\(\large{\tan}\) の加法定理の式は、三角関数の相互関係 の式 $$\large{\tan \theta = \frac{\sin \theta}{\cos \theta}}$$ から求めることができます。

式(1)と式(3)から、 \begin{eqnarray} \large \tan(\alpha +\beta)&\large =&\large \frac{\sin (\alpha +\beta)}{\cos (\alpha +\beta)} \\[0.4em] \large &\large =&\large \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta}\\ \end{eqnarray} となります。
ここで、分母と分子を \(\large{\cos \alpha \cos \beta}\) で割ると、 $$\large{\tan(\alpha +\beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}\hspace{10pt}(5)}$$ が導かれます。

・tan(α-β)の公式

次に、\(\large{\tan(\alpha +\beta)}\) から \(\large{\tan(\alpha -\beta)}\) の公式を導きます

(5)式の角度\(\large{\beta}\) を \(\large{-\beta}\) に置き換えると、三角関数の性質 から \(\large{\tan (-\theta) = -\tan \theta}\) であるため、 \begin{eqnarray} \large \tan(\alpha -\beta)&\large =&\large \frac{\tan \alpha + \tan (-\beta)}{1-\tan \alpha \tan (-\beta)} \\[0.4em] \large &\large =&\large \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta}\hspace{10pt}(6) \\ \end{eqnarray} が導かれます。

【1-2】余弦定理を利用した証明

先述した証明では、2点間の距離の公式から加法定理を求めました。
加法定理の証明には 余弦定理 を使用する方法もあります。本章では、余弦定理を使用した証明について説明します。

下図の単位円に 角度\(\large{\alpha}\) の動径\(\large{\overline{OP}}\)と 角度\(\large{\beta}\) の動径\(\large{\overline{OQ}}\) をとります。

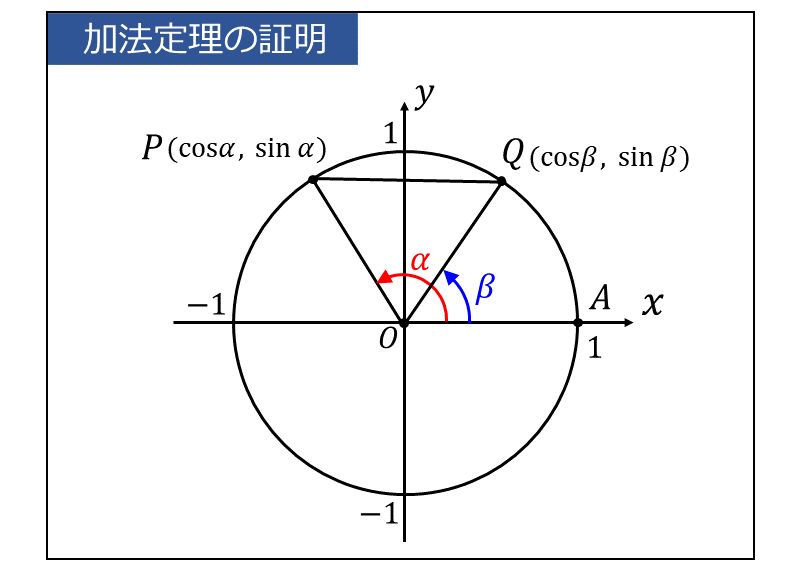
このとき、余弦定理から \(\large{\overline{PQ}}\) の長さを計算すると \begin{eqnarray} \large \overline{PQ}^2 &\large =&\large 1^2 + 1^2 -2\times 1\times1 \times \cos(\alpha-\beta) \\[0.4em] \large &\large =&\large 2 -2\cos(\alpha-\beta)\hspace{10pt}(7) \\ \end{eqnarray} となります。

また、点\(\large{P}\)と点\(\large{Q}\)の2点間の距離\(\large{\overline{PQ}}\)を 2点間の距離の公式から求めると、 \begin{eqnarray} \large \overline{PQ}^2&\large =&\large (\cos \alpha - \cos \beta)^2 + (\sin \alpha - \sin \beta)^2 \\[0.4em] \large &\large =&\large 2-2 (\cos \alpha \cos \beta+\sin \alpha \sin \beta)\hspace{10pt}(8)\\ \end{eqnarray} となります。

(7)式と(8)式を比較すると、 $$\large{\cos(\alpha-\beta) = \cos \alpha \cos \beta+\sin \alpha \sin \beta}$$ が導出されます。

【2】基礎的な問題と解き方

加法定理の基礎的な問題と解き方について解説します。

加法定理を利用すると、ある角度\(\large{\alpha,\hspace{2pt}\beta}\) の三角関数の値が判明していれば、角度\(\large{\alpha+\beta,\hspace{2pt}}\)\(\large{\alpha-\beta}\) の三角関数の値を計算することができます。

この性質を利用して、以下の問題について考えます。

(解答と解説 : 問題(1) 問題(2) 問題(3))

問題(4)～(6)は、度数法によって角度を表現した場合の問題です。

問題(4)～(6)は弧度法により角度を表現した場合の問題です。

(解答と解説 : 問題(4) 問題(5) 問題(6))

問題(1) sin75°の計算問題

以下のような三角関数の値を求めます。

【解答と解説】
問題の三角関数の角度は $$\large{75° = 30°+45°}$$ であるため、加法定理 $$\large{\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta}$$ から以下のように計算されます。

\begin{eqnarray} \large \sin 75°&\large =&\large \sin 30° \cos 45° + \cos 30° \sin 45° \\[0.4em] \large &\large =&\large \frac{1}{2}\frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2}\frac{\sqrt{2}}{2}\\[0.4em] &\large =&\large \frac{\sqrt{2}+\sqrt{6}}{4}\\ \end{eqnarray} となります。

問題(2) cos15°の計算問題

以下のような三角関数の値を求めます。

【解答と解説】
問題の三角関数の角度は $$\large{15° = 45°-30°}$$ であるため、加法定理 $$\large{\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta}$$ から以下のように計算されます。

\begin{eqnarray} \large \cos 15°&\large =&\large \cos 45° \cos 30° + \sin 45° \sin 30° \\[0.4em] \large &\large =&\large \frac{\sqrt{2}}{2}\frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2}\frac{1}{2}\\[0.4em] &\large =&\large \frac{\sqrt{2}+\sqrt{6}}{4}\\ \end{eqnarray} となります。

問題(3) tan105°の計算問題

以下のような三角関数の値を求めます。

【解答と解説】
問題の三角関数の角度は $$\large{105° = 45°+60°}$$ であるため、加法定理 $$\large{\tan(\alpha +\beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}}$$ から以下のように計算されます。

\begin{eqnarray} \large \tan 105°&\large =&\large \frac{\tan 45° + \tan 60°}{1-\tan 45° \tan 60°}\\[0.4em] \large &\large =&\large \frac{1+ \sqrt{3}}{1-1\times \sqrt{3}}\\[0.4em] &\large =&\large -(2+\sqrt{3})\\ \end{eqnarray} となります。

問題(4) sin(π/12)の計算問題

以下のような三角関数の値を求めます。

【解答と解説】
問題の三角関数の角度は弧度法で表されており、 $$\large{\frac{\pi}{12} = \frac{\pi}{4}-\frac{\pi}{6}}$$ であるため、加法定理 $$\large{\sin(\alpha -\beta) =\sin \alpha \cos \beta - \cos \alpha \sin \beta}$$ から以下のように計算されます。

\begin{eqnarray} \large \sin \frac{\pi}{12}&\large =&\large \sin \frac{\pi}{4} \cos\frac{\pi}{6} - \cos \frac{\pi}{4} \sin \frac{\pi}{6} \\[0.4em] \large &\large =&\large \frac{\sqrt{2}}{2}\frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2}\frac{1}{2}\\[0.4em] &\large =&\large \frac{\sqrt{6}-\sqrt{2}}{4}\\ \end{eqnarray} となります。

問題(5) cos(5π/12)の計算問題

以下のような三角関数の値を求めます。

【解答と解説】
問題の三角関数の角度は弧度法で表されており、 $$\large{\frac{5}{12}\pi = \frac{\pi}{4}+\frac{\pi}{6}}$$ であるため、加法定理 $$\large{\cos(\alpha +\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta}$$ から以下のように計算されます。

\begin{eqnarray} \large \cos \frac{5}{12}\pi &\large =&\large \cos \frac{\pi}{4} \cos \frac{\pi}{6} - \sin \frac{\pi}{4} \sin \frac{\pi}{6} \\[0.4em] \large &\large =&\large \frac{\sqrt{2}}{2}\frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2}\frac{1}{2}\\[0.4em] &\large =&\large \frac{\sqrt{6}-\sqrt{2}}{4}\\ \end{eqnarray} となります。

問題(6) tan(11π/12)の計算問題

以下のような三角関数の値を求めます。

【解答と解説】
問題の三角関数の角度は弧度法で表されており、 $$\large{\frac{11}{12}\pi = \frac{\pi}{4} + \frac{2}{3}\pi}$$ であるため、加法定理 $$\large{\tan(\alpha +\beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}}$$ から以下のように計算されます。

\begin{eqnarray} \large \tan \frac{11}{12}\pi&\large =&\large \frac{\tan \frac{\pi}{4} + \tan\frac{2}{3}\pi}{1-\tan\frac{\pi}{4} \tan \frac{2}{3}\pi}\\[0.4em] \large &\large =&\large \frac{1- \sqrt{3}}{1-1\times (-\sqrt{3})}\\[0.4em] &\large =&\large \sqrt{3}-2\\ \end{eqnarray} となります。

【3】応用問題と解き方

加法定理の応用的な問題と解き方について解説します。

(解答と解説 : 問題(7) 問題(8) 問題(9) 問題(10))

問題(7) sinとcosの相互関係

【解答と解説】
まず、問題の条件は \(\large{\sin}\) しか与えられていないため、相互関係の式から \(\large{\cos}\) の値を求めます。

\(\large{\sin^2 \alpha + \cos^2 \alpha = 1}\) より、 $$\large{\cos^2 \alpha = 1-\left( \frac{3}{5}\right)^2 = \frac{16}{25}}$$ ここで、\(\displaystyle\large{0 < \alpha < \frac{\pi}{2}}\) のとき \(\large{\cos \alpha > 0}\) であるため、 $$\large{\cos \alpha = \frac{4}{5}}$$

また、\(\large{\sin^2 \alpha + \cos^2 \alpha = 1}\) より、 $$\large{\cos^2 \beta = 1-\left( \frac{4}{5}\right)^2 = \frac{9}{25}}$$ ここで、\(\displaystyle\large{\frac{\pi}{2}< \beta < \pi}\) のとき \(\large{\cos \beta < 0}\) であるため、 $$\large{\cos \beta = -\frac{3}{5}}$$

以上から、 \begin{eqnarray} \large \sin (\alpha+\beta)&\large =&\large \sin \alpha \cos \beta + \cos \alpha \sin \beta \\[0.4em] \large &\large =&\large \frac{3}{5}\times \left(-\frac{3}{5}\right) + \frac{4}{5}\times\frac{4}{5}\\[0.4em] &\large =&\large \frac{7}{25} \end{eqnarray}

また、\begin{eqnarray} \large \cos (\alpha+\beta)&\large =&\large \cos \alpha \cos \beta - \sin \alpha \sin \beta \\[0.4em] \large &\large =&\large \frac{4}{5}\times \left(-\frac{3}{5}\right) - \frac{3}{5}\times\frac{4}{5}\\[0.4em] &\large =&\large -\frac{24}{25} \end{eqnarray}

問題(8) 条件式から三角関数を計算

【解答と解説】
与えられた条件式を2乗すると、\(\large{\sin \alpha \sin \beta}\) と \(\large{\cos\alpha \cos\beta}\) の項が表れることを利用します。

\(\displaystyle\large \sin \alpha +\sin \beta = \frac{1}{2}\) を2乗すると、 $$\large{\sin^2 \alpha + 2\sin \alpha\sin \beta + \sin^2 \beta = \frac{1}{4}}$$

\(\displaystyle\large \cos\alpha + \cos\beta=\sqrt{2}\) を2乗すると、 $$\large{\cos^2 \alpha + 2\cos \alpha\cos \beta + \cos^2 \beta = 2}$$

2式の両辺を足すと以下のようになります。(相互関係の式 \(\large{\sin^2 \alpha + \cos^2 \alpha = 1}\) を使用しています。) $$\large{2+2(\cos \alpha\cos \beta+\sin \alpha\sin \beta) = \frac{9}{4}}$$ ここで、 $$\large{\cos(\alpha -\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta}$$ であるため、 $$\large{2+2\cos(\alpha -\beta) = \frac{9}{4}}$$ すなわち $$\large{\cos(\alpha -\beta) = \frac{1}{8}}$$ と求められます。

問題(9) 3つのtanの値から角度の導出

【解答と解説】
まず、\(\large{\tan}\) の加法定理から \(\large{\tan(\alpha+\beta)}\) の値を求めます。 $$\large{\tan(\alpha +\beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta}}$$ であるので、 $$\large{\tan(\alpha +\beta) = \frac{2 + 4}{1-2 \times 4}=-\frac{6}{7}}$$ となります。

次に、\(\large{\tan(\alpha+\beta+\gamma)}\) の値を求めます。
$$\large{\tan \{(\alpha +\beta)+\gamma\} = \frac{-\frac{6}{7} + 13}{1-(-\frac{6}{7}) \times 13}=1}$$

ここで、 $$\large{\sqrt{3}<\tan \alpha<\tan \beta<\tan \gamma}$$ であることと、\(\large{\alpha,\hspace{5pt}\beta,\hspace{5pt}\gamma}\) が鋭角であるという条件から、\(\displaystyle\large{\tan \frac{\pi}{3}=\sqrt{3}}\) より $$\large{\frac{\pi}{3} <\alpha < \beta < \gamma < \frac{\pi}{2}}$$ が成り立ちます。
すなわち、

$$\large{\pi <\alpha + \beta + \gamma < \frac{3}{2}\pi}$$ を満たします。
この条件で \(\large{\tan (\alpha + \beta + \gamma)=1}\) を解くと、 $$\large{\alpha + \beta + \gamma = \frac{5}{4}\pi}$$ となります。

問題(10) tanの加法定理を利用した直線の傾き

以下のような三角関数の値を求めます。

【解答と解説】
問題の2つの直線を図に書くと以下のようになります。

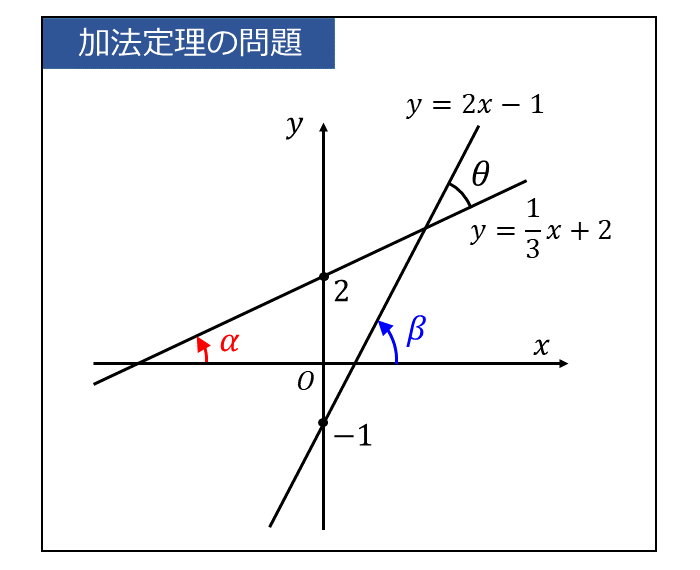
図より、\(\large{x}\)軸から反時計回りに計った角度を \(\large{\alpha,\hspace{2pt}}\)\(\large{\beta}\) とすると、\(\large{\theta = \beta - \alpha}\) となります。

このとき、\(\large{\tan \alpha,\hspace{2pt}}\)\(\large{\tan \beta}\) は直線の傾きを表すので、 $$\large{\tan \alpha = \frac{1}{3}}$$ $$\large{\tan \beta = 2}$$ が成り立ちます。

したがって、\(\large{\tan}\) の加法定理 $$\large{\tan \theta = \tan(\beta -\alpha) = \frac{\tan \beta - \tan \alpha}{1+\tan \beta \tan \alpha}}$$ から以下のように計算されます。

\begin{eqnarray} \large \tan \theta&\large =&\large \frac{2 -\frac{1}{3}}{1+2 \times \frac{1}{3}}\\[0.4em] &\large =&\large 1\\ \end{eqnarray} となります。

図から、\(\large{0 < \theta < \frac{\pi}{2}}\) であるため、角度\(\large{\theta}\)は $$\large{\theta = \frac{\pi}{4}}$$ と求められます。

---