多光束干渉とは -反射防止膜の計算-
本項では以下の内容を解説しています。
- ・多光束干渉と反射防止膜の解説
- ・単層の反射防止膜の計算
- ・反射防止膜の反射率、透過率
【1】多光束干渉と反射防止膜
薄膜の干渉の項では、薄膜の表面と裏面の2つの経路の光の干渉のみを考えていました。2つに分割された光の干渉を、二光束干渉といいます。
一方、薄膜内の内部反射を無視できない場合などは、多くの経路に分割された光の干渉について考える必要があります。複数に分割された光同士の干渉を多光束干渉といいます。
多光束干渉を利用し、反射率(もしくは透過率)を制御する技術として反射防止膜が知られています。
本項では、多光束干渉の例として、反射防止膜を取り上げ、反射率や透過率の計算について解説します。
【1-1】薄膜での多光束干渉
図1にガラス上の薄膜に光が入射し、多光束干渉が発生する場合の光の経路を図示します。
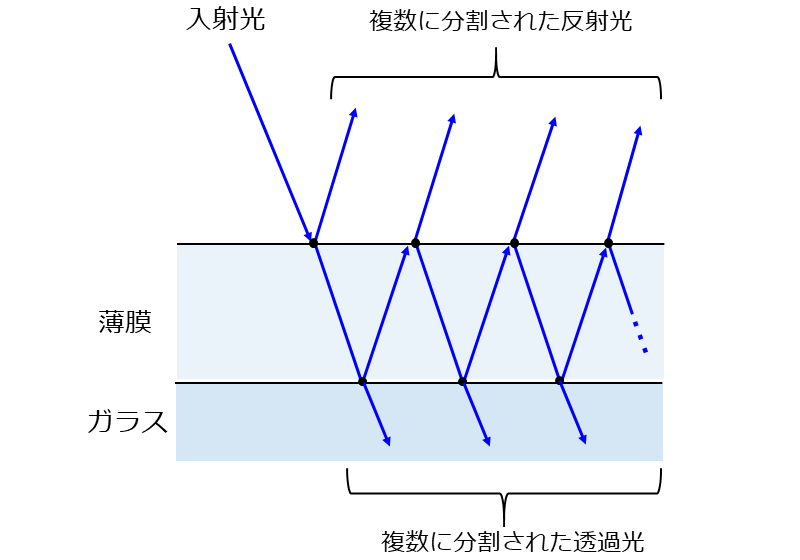
図1では、膜の表面と裏面で内部反射を繰り返し、入射側に複数の反射光が存在しています。
このとき、反射光は伝搬した経路に応じて位相が変化するため、異なる経路の反射光同士が干渉し、反射光の光強度の強め合いや弱め合いが発生します。
また、薄膜を透過したガラス側にも異なる径路の透過光が複数存在し、透過光の光強度の強め合い、弱め合いが発生します。
【1-2】反射防止膜とは
ガラスや水などは一見すると透明な物質ですが、その表面では少なからず反射が発生しています。
例えば、屈折率が\(\hspace{2pt}\large{n=1.5}\hspace{2pt}\)のガラスでは、その表面で入射した光の約\(\hspace{2pt}\large{4}\hspace{2pt}\)%を反射しています。
カメラレンズや顕微鏡といった光学製品では、多くのレンズの組み合わせによって光学系を構成しており、\(\hspace{2pt}\large{4}\hspace{2pt}\)%の反射率でも、繰り返し反射されることで光は大きく減衰してしまいます。
例えば、\(\hspace{2pt}\large{10}\hspace{2pt}\)枚のレンズを並べた場合、その表面と裏面で光が反射するため、\(\hspace{2pt}\large{0.96^{20}=0.44}\hspace{2pt}\)から入射光の\(\hspace{2pt}\large{44}\hspace{2pt}\)%にまで光強度が減衰してしまいます。
反射防止膜とは、反射による光強度の減衰を抑えるため、ガラスレンズの表面に薄い膜を形成することで光の干渉を制御し、反射率を大幅に低減させる薄膜のことをいいます。
例えば、最も単純な構成の単層膜(1層の膜)による反射防止膜でも、特定の光の波長においては反射率を計算上ゼロにまで低減させることができます。
(ただし、単層膜では反射率をゼロ近くまで低減できるガラスと膜材の組み合わせは限られています。この点については【2-5】単層膜の実用上の問題点で後述しています。)
次の章では、反射防止膜の最も簡単な例である単層膜を例として、反射率の計算について解説します。
【2】単層膜の反射率の計算
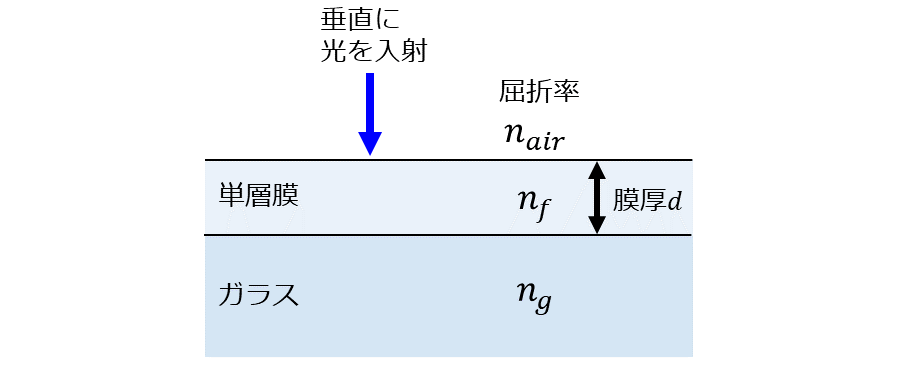
図2のように、屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\)のガラスに屈折率\(\hspace{2pt}\large{n_{f}}\hspace{2pt}\)の単層膜が形成されているとします。
この単層膜に、屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\)の媒質から垂直に光を入射したときの反射率の計算と、その反射率がゼロとなる条件について解説します。
【2-1】振幅反射係数と振幅透過係数の計算
まず、反射率の計算の準備として、振幅反射係数と振幅透過係数を計算します。
振幅反射係数と振幅透過係数とは、物質の境界面での入射光の電場\(\hspace{2pt}\large{E_0}\hspace{2pt}\)に対する、反射波と透過波の電場の振れ幅の比を与える係数です。
反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)は、入射光と反射光の電場の比の2乗で計算されるため、振幅反射係数を求めることで、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)を計算することができます。
(振幅反射係数と振幅透過係数はフレネルの公式により計算される値です。フレネルの公式については別ページに解説しています。)
フレネルの公式より、屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\)の領域から、屈折率\(\hspace{2pt}\large{n_f}\hspace{2pt}\)の単層膜に、垂直に光が入射したときの振幅反射係数\(\hspace{2pt}\large{r_0}\hspace{2pt}\)と振幅透過係数\(\hspace{2pt}\large{t_0}\hspace{2pt}\)は、以下のようになります。 \begin{eqnarray} \large r_0&\large =&\large \frac{n_{air} - n_f}{n_{air} + n_f}\\ \large t_0&\large =&\large \frac{2 n_{air}}{n_{air} + n_f}\\ \end{eqnarray}
また、屈折率\(\hspace{2pt}\large{n_f}\hspace{2pt}\)の単層膜から、屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\)のガラス面の境界に入射するときの振幅反射係数\(\hspace{2pt}\large{r_1}\hspace{2pt}\)と振幅透過係数\(\hspace{2pt}\large{t_1}\hspace{2pt}\)は以下のようになります。 \begin{eqnarray} \large r_1&\large =&\large \frac{n_f - n_g}{n_f + n_g}\\ \large t_1&\large =&\large \frac{2 n_f}{n_f + n_g}\\ \end{eqnarray}
また、屈折率\(\hspace{2pt}\large{n_f}\hspace{2pt}\)の単層膜内から、屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\)の領域に入射するときの振幅反射係数\(\hspace{2pt}\large{r'_1}\hspace{2pt}\)と振幅透過係数\(\hspace{2pt}\large{t'_1}\hspace{2pt}\)は以下のようになります。 \begin{eqnarray} \large r'_1&\large =&\large \frac{n_f - n_{air}}{n_f + n_{air}} = -r_0\\ \large t'_1&\large =&\large \frac{2 n_f}{n_f + n_{air}}\\ \end{eqnarray}
【2-2】膜内での位相変化
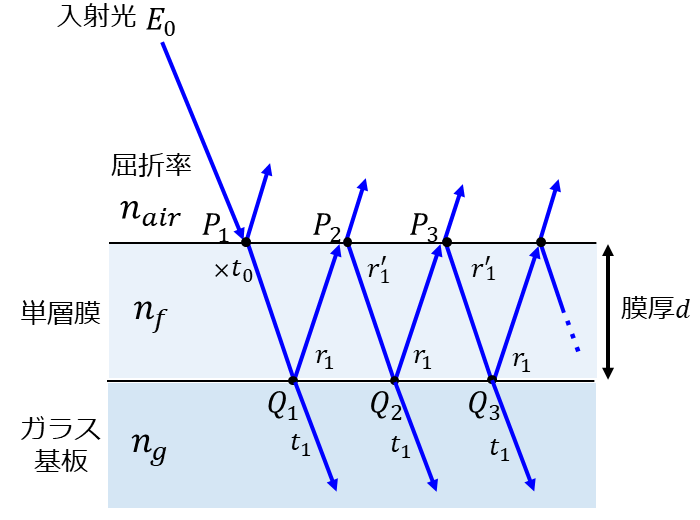
図3に示すように、単層膜に入射した光線が単層膜とガラスの境界で多重反射する成分をすべて足し合わせることにより、反射光の電場を求めることができます。
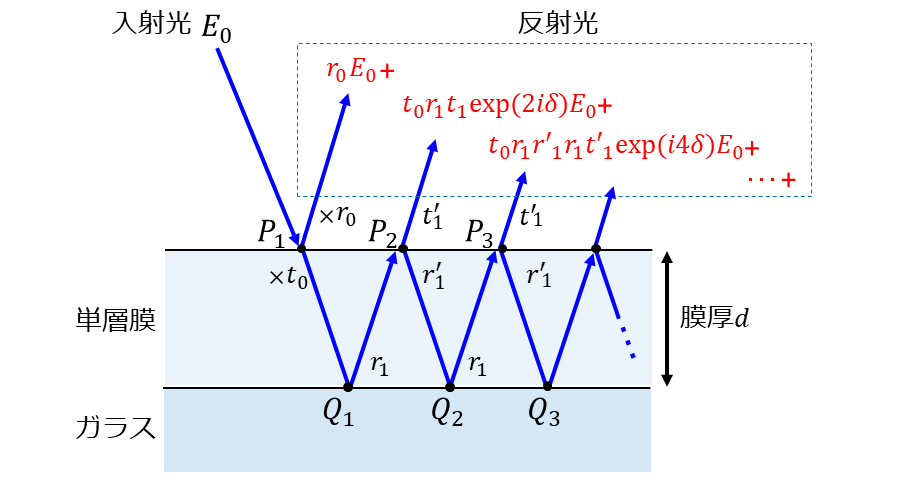
振れ幅\(\hspace{2pt}\large{E_0}\hspace{2pt}\)の入射光が単層膜に入射したとすると、\(\hspace{2pt}\large{P_1}\hspace{2pt}\)点で反射した光の電場の振れ幅は\(\hspace{2pt}\large{r_0 E_0}\hspace{2pt}\)、透過した電場の振れ幅は\(\hspace{2pt}\large{t_0 E_0}\hspace{2pt}\)となります。
また、\(\hspace{2pt}\large{Q_1}\hspace{2pt}\)点で反射して、\(\hspace{2pt}\large{P_2}\hspace{2pt}\)点で透過した場合、その光の振れ幅は\(\hspace{2pt}\large{t_0 r_1 t'_1 E_0 \exp{(i 2 \delta)}}\hspace{2pt}\)となります。
\(\hspace{2pt}\large{\exp{(i 2 \delta)}}\hspace{2pt}\)は、光が膜中を往復する間に発生する位相変化を表す項です。
点\(\hspace{2pt}\large{P_1}\hspace{2pt}\)から点\(\hspace{2pt}\large{P_2}\hspace{2pt}\)までの光路差は、垂直入射の場合\(\hspace{2pt}\large{2 n_f d}\hspace{2pt}\)です。したがって、光路差を位相差に換算すると以下のようになります。
\begin{eqnarray}
\large 2 \delta&\large =&\large \frac{2 \pi}{\lambda} \times 2 n_f d \\
&\large =&\large \frac{4 \pi}{\lambda} n_f d \\
\end{eqnarray}
(薄膜の光路差については薄膜の干渉で解説しています。)
【2-3】反射率Rの計算
以上から、単層膜から反射する電場の総和を計算することで、反射率を求めます。入射光の電場が\(\hspace{2pt}\large{E_0}\hspace{2pt}\)、反射光の総和を\(\hspace{2pt}\large{E_r}\hspace{2pt}\)とすると、\(\hspace{2pt}\large{E_r}\hspace{2pt}\)は以下のようになります。
上式の計算では、\(\hspace{2pt}\large{t_0 t_1 = 1-{r_0}^2}\hspace{2pt}\)と\(\hspace{2pt}\large{r'_1 = -r_0}\hspace{2pt}\)の関係を使用しています。
したがって、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)は以下のようになります。
【2-4】反射率Rがゼロとなる条件の導出
ここで、上記の計算から反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)がゼロであるとき、以下の式が成り立ちます。 $$\large{r_0 + r_1 \exp{(i 2\delta)} = 0}$$
上式から、以下の2式を満たすときに反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)がゼロとなることが分かります。
\(\hspace{2pt}\large{\displaystyle r_0 = r_1\hspace{25pt}(1)}\hspace{2pt}\)
\(\hspace{2pt}\large{\displaystyle 2\delta = (2m-1) \pi\hspace{10pt}(m=1,2,\cdots)\hspace{5pt}(2)}\hspace{2pt}\)
(1)式は、反射振幅係数に関する条件式です。反射振幅係数は物質の屈折率により決定されるため、(1)式は単層膜とガラスの屈折率に関する条件を与えます。
一方、(2)式は、膜内での位相変化に関する条件式です。位相変化の大きさは、(1)式で屈折率が決定されれば、膜厚\(\hspace{2pt}\large{d}\hspace{2pt}\)によって決まる値です。したがって、(2)式は単層膜の膜厚\(\hspace{2pt}\large{d}\hspace{2pt}\)に関する条件を与える式です。
したがって、(1),(2)式から特定の波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)とガラスの屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\)に対して、反射率をゼロにする単層膜の屈折率\(\hspace{2pt}\large{n_f}\hspace{2pt}\)と膜厚\(\hspace{2pt}\large{d}\hspace{2pt}\)を導くことができます。
屈折率の条件
(1)式から屈折率の条件を求めると、\(\hspace{2pt}\large{r_0 = r_1}\hspace{2pt}\)を満たす屈折率は以下のようになります。 $$\large{n_{air} n_g = {n_f}^2}$$
特に、空気中\(\hspace{2pt}\large{n_{air}=1}\hspace{2pt}\)であるとき、単層膜の屈折率\(\hspace{2pt}\large{n_f}\hspace{2pt}\)とガラスの屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\)の関係は以下のようになります。 $$\large{n_f = \sqrt{n_g}}$$
膜厚の条件
また、単層膜の膜厚に関する条件を求めると、\(\hspace{2pt}\large{2\delta = (2m-1) \pi}\hspace{2pt}\)を満たす膜厚は、以下のように求められます。 $$\large{2\delta = \frac{4 \pi}{\lambda} n_f d = 2(m-1) \pi}$$ したがって、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)がゼロとなる膜厚の条件は、以下となります。 $$\large{n_f d = \frac{2m-1}{4}\lambda}$$
単層膜により反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)をゼロにする条件をまとめると、以下のようになります。
\(\hspace{2pt}\large{\displaystyle n_f = \sqrt{n_g}\hspace{10pt}(1)'}\hspace{2pt}\)
\(\hspace{2pt}\large{\displaystyle n_f d = \frac{2m-1}{4}\lambda\hspace{10pt}(m=1,2,\cdots)\hspace{5pt}(2)'}\hspace{2pt}\)
ここで、図4に(1)'式(\(\hspace{2pt}\large{n_f = \sqrt{n_g}}\hspace{2pt}\))を満たすとき、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)を縦軸、光学膜厚\(\hspace{2pt}\large{n_f d}\hspace{2pt}\)を横軸に取ったときのグラフを示します。
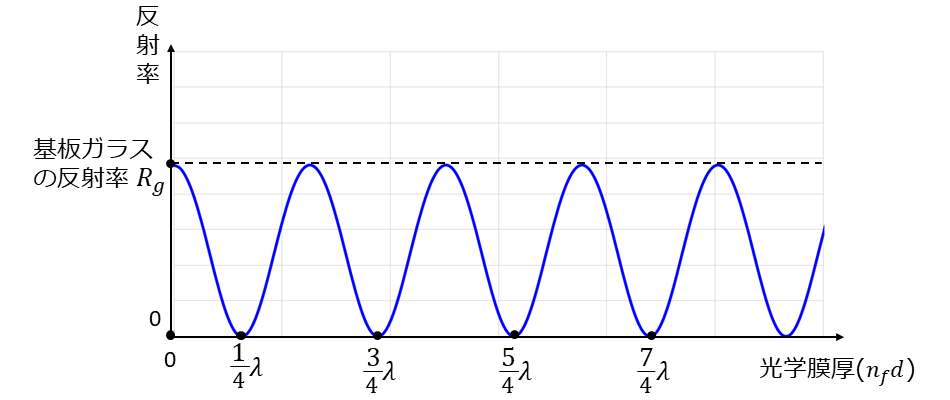
図4から、光学膜厚\(\hspace{2pt}\large{n_f d}\hspace{2pt}\)は\(\hspace{2pt}\large{\frac{1}{4}\lambda}\hspace{2pt}\)の厚みのとき最小値を取り、光学膜厚が\(\hspace{2pt}\large{\frac{1}{2}\lambda}\hspace{2pt}\)だけ増加するごとに反射率がゼロとなっていることが分かります。
(光学膜厚\(\hspace{2pt}\large{n_f d=0}\hspace{2pt}\)は膜厚がゼロのとき、すなわち膜が存在しない状態を表します。その場合は、空気とガラス間の反射率\(\hspace{2pt}\large{R_g}\hspace{2pt}\)となります。)
【2-5】単層膜の実用上の問題点
単層膜を反射防止膜として使用するときに問題となるのは、式(1)'の\(\hspace{2pt}\large{n_f = \sqrt{n_g}}\hspace{2pt}\)の条件を満たすガラスと膜材の組み合わせが限られるところにあります。
例えば、\(\hspace{2pt}\large{MgF_2}\hspace{2pt}\)は最も屈折率の低い膜材として知られており、その屈折率は約1.38です。
\(\hspace{2pt}\large{MgF_2}\hspace{2pt}\)の屈折率から、(1)'式より反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)をゼロにするガラスの屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\)を計算すると、以下のようになります。
$$\large{n_g = {n_f}^2 = {1.38}^2 \approx 1.90}$$
光学レンズ用に使用されるガラスの屈折率は約1.4~2.1の間にあり、1.9より小さい屈折率を持つガラスでは、反射率を十分に低減させることができなくなります。
図5に、\(\hspace{2pt}\large{MgF_2}\hspace{2pt}\)の単層膜と、屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\)を3パターン(\(\hspace{2pt}\large{n_g=1.9,1.7,1.5}\hspace{2pt}\))で計算した結果を示します。
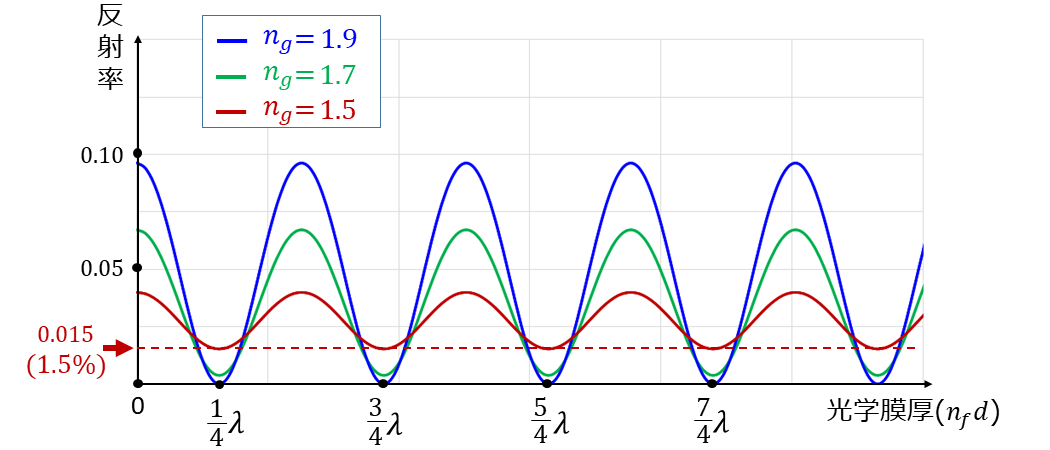
図5より、\(\hspace{2pt}\large{n_g=1.5}\hspace{2pt}\)であるとき、最も低い反射率が約1.5%となり、完全に反射をゼロにできていないことが分かります。
上記のような問題を解決するためには、単層膜ではなく、異なる種類の膜材を層状に重ねた多層膜を成膜する必要があります。
【3】多光束干渉と反射防止膜の計算
本章では、反射防止膜の膜厚計算や透過率の計算について解説します。
【3-1】単層膜の膜厚の計算
【問題】
屈折率\(\hspace{2pt}\large{n_g = 1.9}\hspace{2pt}\)のガラス基板に、屈折率\(\hspace{2pt}\large{n_f=1.38}\hspace{2pt}\)の単層膜を成膜する。単層膜に垂直に光を入射したとき、d線(\(\hspace{2pt}\large{\lambda=589.3[nm]}\hspace{2pt}\))における反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)を最も小さくするための、膜厚\(\hspace{2pt}\large{d}\hspace{2pt}\)の条件を求めよ。
また、条件を満たす最も薄い膜厚\(\hspace{2pt}\large{d_{min}}\hspace{2pt}\)を求めよ。
【解答と解説】
(2)'式より、反射率を最も小さくする光学膜厚\(\hspace{2pt}\large{n_f d}\hspace{2pt}\)は以下の式により求められます。
$$\large{n_f d = \frac{2m-1}{4}\lambda}$$
したがって、膜の厚み\(\hspace{2pt}\large{d}\hspace{2pt}\)について解いた以下が反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)が最小の条件となります。 $$\large{d = \frac{2m-1}{4 n_f}\lambda}$$
また、\(\hspace{2pt}\large{m=1}\hspace{2pt}\)のとき、膜厚が最小となるため、最も薄い膜厚\(\hspace{2pt}\large{d_{min}}\hspace{2pt}\)は以下のようになります。 $$\large{d_{min} = \frac{1}{4 \times 1.38}\times 589.3 \approx 107[nm] }$$
【3-2】透過率の計算
【問題】
図6のように、ガラス基板(屈折率\(\hspace{2pt}\large{n_g}\hspace{2pt}\))に単層膜(屈折率\(\hspace{2pt}\large{n_f}\hspace{2pt}\))が成膜されているとする。空気中(屈折率\(\hspace{2pt}\large{n_{air}}\hspace{2pt}\))から垂直に、光が入射したときのガラス基板側に透過する透過率\(\hspace{2pt}\large{T}\hspace{2pt}\)を求めよ。
【解答と解説】
単層膜の透過率\(\hspace{2pt}\large{T}\hspace{2pt}\)は、反射率\(\hspace{2pt}\large{R}\hspace{2pt}\)を求めたときと同様に、多層膜内の多重反射のうち透過する成分を全て足し合わせて計算します。
図7に、多層膜からガラス基板側に射出される電場成分を図示します。
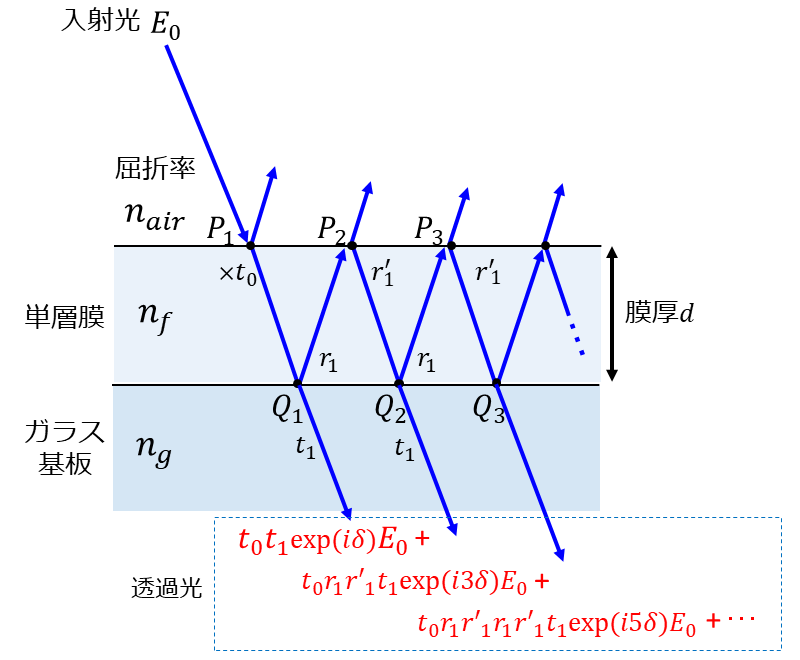
振れ幅\(\hspace{2pt}\large{E_0}\hspace{2pt}\)の入射光が単層膜に入射すると、\(\hspace{2pt}\large{P_1}\hspace{2pt}\)点を透過した光の電場の振れ幅は\(\hspace{2pt}\large{t_0 E_0}\hspace{2pt}\)となります。さらに、\(\hspace{2pt}\large{Q_1}\hspace{2pt}\)点を透過した光の電場の振れ幅は、\(\hspace{2pt}\large{t_0 t_1 \exp{(i \delta)} E_0}\hspace{2pt}\)となります。
また、\(\hspace{2pt}\large{Q_1}\hspace{2pt}\)点を反射した光は、\(\hspace{2pt}\large{P_2}\hspace{2pt}\)点を反射した後、\(\hspace{2pt}\large{Q_2}\hspace{2pt}\)点において透過光と反射光に分かれます。このとき、\(\hspace{2pt}\large{Q_2}\hspace{2pt}\)点における透過光の振れ幅は、\(\hspace{2pt}\large{t_0 r_1 r'_1 t_1 \exp{(i 3 \delta)}}\hspace{2pt}\)となります。
反射光と同様に、透過する電場を全て足し合わせることにより、透過率を求めます。
上式の計算では、\(\hspace{2pt}\large{t_0 t_1 = 1-{r_0}^2}\hspace{2pt}\)と\(\hspace{2pt}\large{r'_1 = -r_0}\hspace{2pt}\)の関係を使用しています。
したがって、透過率Tは以下のようになります。