-光と光学に関連する用語の解説サイト-

フレネルの公式

フレネルの公式とは、屈折率の異なる媒質の境界面に光が入射したときの反射光、透過光の電場の振幅の比を計算する公式です。

本項では、以下の内容について解説します。

・p偏光とs偏光とは
・フレネルの公式
・境界面の反射率

また、フレネルの公式による反射率と透過率,ブリュースター角を計算するツールを別のページで作成しています。

1. p偏光とs偏光
2. 振幅反射係数と振幅透過係数
3. フレネルの公式と反射率の計算
参考文献

【1】s偏光とp偏光

フレネルの公式では、境界面に対して斜めに入射する光を扱います。

斜め入射では、光は電場Eの振動方向によってs偏光もしくはp偏光と呼ばれる2つの偏光の状態に分けられます。
本章では、s偏光とp偏光について解説します。

【1-1】p偏光

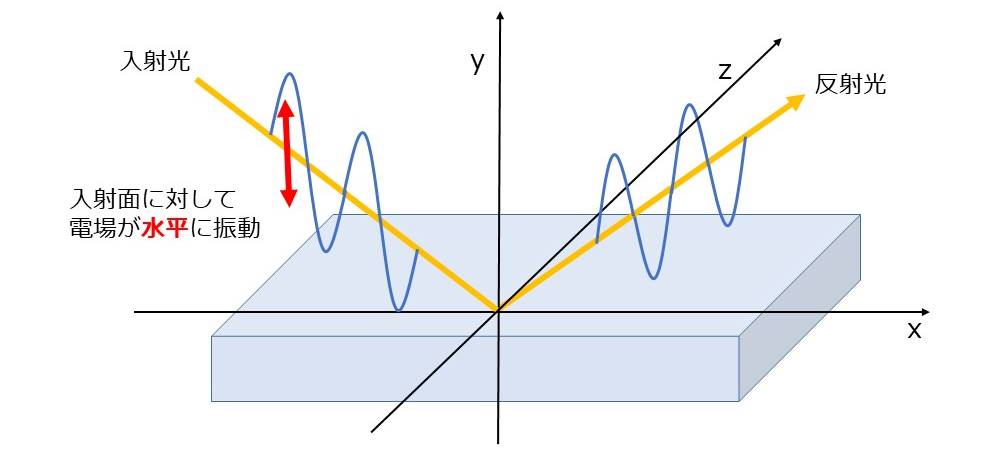
下記の図1に、p偏光の電場の振動の様子のイメージを示します。

図1では、xz平面が屈折率の異なる物質間の境界面、xy平面が光の入射する入射面を表しています。

図1のように、入射面(図1中のxy平面)に電場が平行に振動している偏光をp偏光といいます。 p偏光のpとは、parallel(平行)を意味しています。

また、p偏光はTM波(transverse magnetic wave)という言い方をする場合もあります。 s偏光のイメージ図

図1.p偏光のイメージ図

【1-2】s偏光

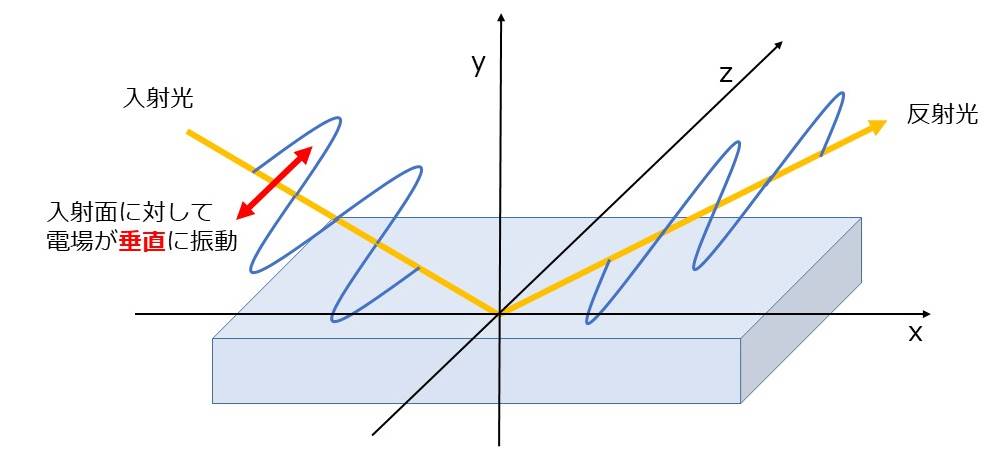
下記の図2に s偏光の電界の振動の様子のイメージを示します。
図2のように、入射面(図中のxy平面)に垂直に振動している偏光をs偏光といいます。s偏光のsは、ドイツ語のsenkrechtの頭文字であり、垂直を意味しています。

s偏光は、TE波(transverse electric wave)という言い方をする場合もあります。 p偏光のイメージ図

図2.s偏光のイメージ図

【2】フレネルの公式とは - 振幅反射係数と振幅透過係数

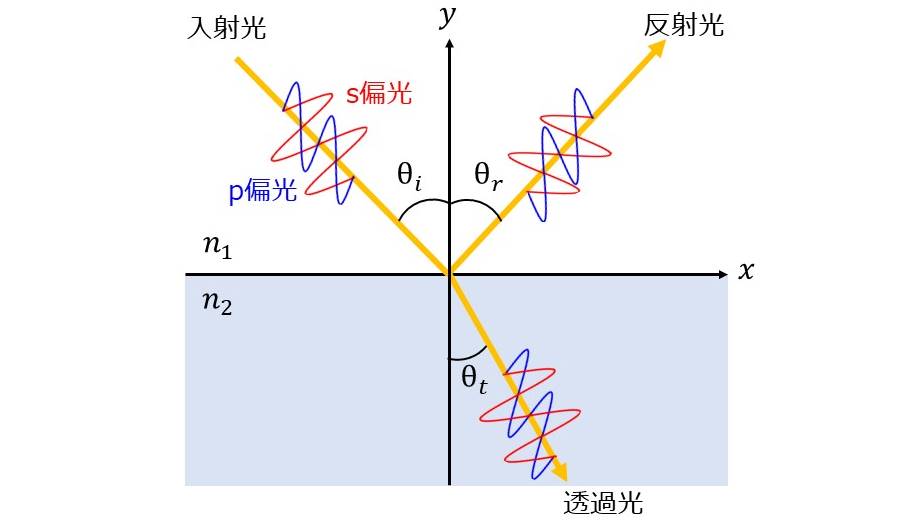
図3のように、屈折率の異なる物質間の境界に光が入射したとき、反射光と透過光が生じます。

図中では、入射光側の媒質の屈折率を$\hspace{2pt}\large{n_1}\hspace{2pt}$、透過光側の媒質の屈折率を$\hspace{2pt}\large{n_2}\hspace{2pt}$とします。また、入射角を$\hspace{2pt}\large{\theta_i}\hspace{2pt}$、屈折角を$\hspace{2pt}\large{\theta_t}\hspace{2pt}$としています。境界面における反射光と透過光

図3.境界面における反射光と透過光

境界面に対する電場、磁場の境界条件から、入射波に対する反射波と透過波の電場の振れ幅の比を求めることができます。この振れ幅の比を振幅反射係数、振幅透過係数といいます。

s偏光、p偏光に対応する振幅反射係数($\hspace{2pt}\large{r_s\hspace{2pt},\hspace{2pt}r_p}\hspace{2pt}$)および振幅透過係数($\hspace{2pt}\large{t_s\hspace{2pt},\hspace{2pt}t_p}\hspace{2pt}$)を(1)～(4)式に示します。
以下の式をフレネルの公式(Fresnel equations)と呼びます。
(フレネルの公式の導出については別のページで解説しています。)

【フレネルの公式】

$$\begin{align} \large r_s=\frac{n_1\cos\theta_i-n_2\cos\theta_t}{n_1\cos\theta_i+n_2\cos\theta_t}\hspace{20pt}(1)\\\\ \large r_p=\frac{n_2\cos\theta_i-n_1\cos\theta_t}{n_2\cos\theta_i+n_1\cos\theta_t}\hspace{20pt}(2)\\\\ \large t_s=\frac{2n_1\cos\theta_i}{n_1\cos\theta_i+n_2\cos\theta_t}\hspace{20pt}(3)\\\\ \large t_p=\frac{2n_1\cos\theta_i}{n_2\cos\theta_i+n_1\cos\theta_t}\hspace{20pt}(4) \end{align}$$

(1)～(4)式はスネルの法則$\hspace{2pt}\large{(n_1\sin\theta_i=n_2\sin\theta_t)}\hspace{2pt}$を使用して、入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$と屈折角$\hspace{2pt}\large{\theta_t}\hspace{2pt}$のみで表現した(1)'～(4)'に変換することができます。

【フレネルの公式(入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$と屈折角$\hspace{2pt}\large{\theta_t}\hspace{2pt}$で表記)】

$$\begin{align} \large r_s=-\frac{\sin(\theta_i-\theta_t)}{\sin(\theta_i+\theta_t)}\hspace{30pt}(1)'\\\\ \large r_p=\frac{\tan(\theta_i-\theta_t)}{\tan(\theta_i+\theta_t)}\hspace{30pt}(2)'\\\\ \large t_s=\frac{2\cos\theta_i\sin\theta_t}{\sin(\theta_i+\theta_t)}\hspace{30pt}(3)'\\\\ \large t_p=\frac{2\cos\theta_i\sin\theta_t}{\sin(\theta_i+\theta_t)\cos(\theta_i-\theta_t)}\hspace{10pt}(4)' \end{align}$$

【3】フレネルの公式と反射率の計算

反射率は、入射光の光強度に対する反射光の光強度の比で定義されます。

光強度は電場の2乗と比例する関係にあるため、 s偏光の反射率$\hspace{2pt}\large{R_s }\hspace{2pt}$とp偏光の反射率$\hspace{2pt}\large{R_p }\hspace{2pt}$は、フレネルの公式で示された振幅反射率の2乗によって、以下のように求められます。

$$\large{R_s=|r_s|^2}$$ $$\large{R_p=|r_p|^2}$$

【3-1】外部反射($\hspace{2pt}\large{n_1 < n_2}\hspace{2pt}$)の反射率

入射側$\hspace{2pt}\large{n_1}\hspace{2pt}$が低屈折率、屈折側$\hspace{2pt}\large{n_2}\hspace{2pt}$が高屈折率の条件で反射する場合を、外部反射(External reflection)といいます。
(例えば、『空気から水』、『空気からガラス』に光が入射する場合を外部反射といいます。)

図4に外部反射の条件で境界面に光が入射した場合($\hspace{2pt}\large{n_1 < n_2}\hspace{2pt}$)の、p偏光とs偏光の反射率を示します。

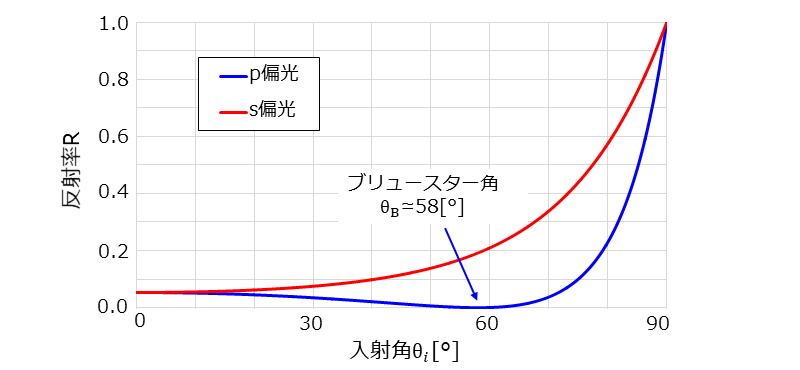
グラフは横軸に入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$[°]、縦軸に反射率$\hspace{2pt}\large{R }\hspace{2pt}$を取っています。図4では、空気($\large{\hspace{2pt}n=1.0\hspace{2pt}}$)から光学ガラス($\large{\hspace{2pt}n=1.6\hspace{2pt}}$)に光が入射した条件で計算をしています。外部反射(空気から光学ガラスに光が入射したとき)の反射率

図4.外部反射(空気から光学ガラスに光が入射したとき)の反射率

図4のp偏光では、反射率がゼロとなる入射角が存在します。反射率がゼロとなる入射角$\hspace{2pt}\large{\theta_B}\hspace{2pt}$をブリュースター角といいます。このブリュースター角の詳細は後述しています。
(また、別ページにブリュースター角の原理や応用について記載しています。)

【3-2】内部反射($\hspace{2pt}\large{n_1 > n_2}\hspace{2pt}$)の反射率

入射側$\hspace{2pt}\large{n_1}\hspace{2pt}$が高屈折率、屈折側$\hspace{2pt}\large{n_2}\hspace{2pt}$が低屈折率の条件で反射する場合を、内部反射(Internal reflection)といいます。
(例えば、『水から空気』、『ガラスから空気』に光が入射する場合を内部反射といいます。)

図5に内部反射の条件で境界面に光が入射した場合($\hspace{2pt}\large{n_1 > n_2}\hspace{2pt}$)のp偏光とs偏光の反射率のグラフを示します。
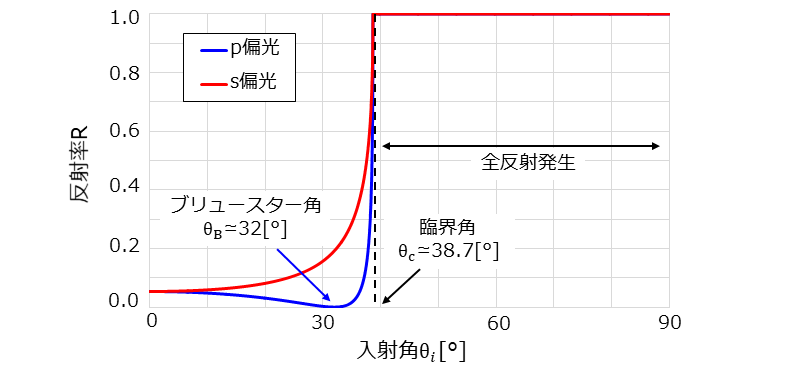
図5は、図4とは反対に光学ガラス($\large{\hspace{2pt}n=1.6\hspace{2pt}}$)から空気($\large{\hspace{2pt}n=1.0\hspace{2pt}}$)に光が入射した条件で計算をしています。内部反射(光学ガラスから空気に光が入射したとき)の反射率

図5.内部反射(光学ガラスから空気に光が入射したとき)の反射率

図4と同様に、p偏光では反射率がゼロとなる入射角であるブリュースター角$\hspace{2pt}\large{\theta_B}\hspace{2pt}$が存在します。

また、内部反射の場合は、ある角度より入射角が大きくなると、反射率が$\large{\hspace{2pt}R = 1\hspace{2pt}}$となる全反射という現象が発生します。

全反射が発生する角度を臨界角といい、$\large{\theta_c\hspace{2pt}}$という記号で表します。
(別ページに全反射の計算や応用について記載しています。)

図4,図5のグラフから、境界面における反射率Rの特徴を述べていきます。

【3-3】垂直入射の反射率の公式

垂直入射(入射角$\hspace{2pt}\large{\theta_i=0}\hspace{2pt}$)では、電場の振動方向が常に境界面に平行なので、s偏光とp偏光という区別がなくなります。
そのため、グラフ上で入射角$\hspace{2pt}\large{\theta_i=0}\hspace{2pt}$において、反射率Rは1つの値を取ります。

フレネルの公式で$\hspace{2pt}\large{\theta_i=\theta_t=0}\hspace{2pt}$とすることで、垂直入射の反射率の公式は以下のように求めることができます。

【垂直入射の反射率の公式】

$\hspace{2pt}\large{\displaystyle R=\left( \frac{n_1 - n_2}{n_1 + n_2}\right)^2}\hspace{2pt}$

【3-4】ブリュースター角$\hspace{2pt}\large{\theta_B}\hspace{2pt}$(偏光角)

s偏光の反射率Rは入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$に対して単調に増加します。

一方で、p偏光の反射率$\hspace{2pt}\large{R}\hspace{2pt}$は入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$が0度から増加するにしたがって減少し、ある特定の角度で$\hspace{2pt}\large{R=0}\hspace{2pt}$になります。

この反射率Rがゼロになる入射角$\hspace{2pt}\large{\theta_B}\hspace{2pt}$をブリュースター角(Brewster's angle)または偏光角(Polarization angle)といいます。

以下の(2)'式から、入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$と屈折角$\hspace{2pt}\large{\theta_t}\hspace{2pt}$の和が90度に等しくなる角度で$\hspace{2pt}\large{r_p=0}\hspace{2pt}$、すなわち反射率$\hspace{2pt}\large{R=0}\hspace{2pt}$となることが分かります。

$$\large{r_p=-\frac{\tan(\theta_i-\theta_t)}{\tan(\theta_i+\theta_t)}\hspace{30pt}(2)'}$$

ブリュースター角は、スネルの法則($\hspace{2pt}\large{n_1 \sin \theta_i = n_2 \sin \theta_t }\hspace{2pt}$)に入射角$\hspace{2pt}\large{\theta_i}\hspace{2pt}$と屈折角$\hspace{2pt}\large{\theta_t}\hspace{2pt}$の和が90度という条件を与えて計算することができます。

\begin{eqnarray} \large \displaystyle n_1 \sin \theta_B &\large =&\large n_2 \sin \theta_t\\[0.7em] \large \displaystyle \theta_B + \theta_t &\large =&\large 90^{ \circ }\\ \end{eqnarray}

2式をブリュースター角$\hspace{2pt}\large{\theta_B}\hspace{2pt}$について解くと、以下の式が得られます。

$$\large{\theta_B=\tan^{-1} \left(\frac{n_2}{n_1}\right)}$$

例えば、図4の反射率Rを計算した$\hspace{2pt}\large{n_1 = 1.0}\hspace{2pt}$, $\hspace{2pt}\large{n_2 = 1.6}\hspace{2pt}$の場合では、ブリュースター角は58度となります。

【3-5】内部全反射

図5では、ある特定の入射角より大きくなるとs偏光、p偏光ともに反射率Rが1となり、入射光のパワーをすべて反射するようになります。

この入射光のパワーをすべて反射する現象を内部全反射(Total internal reflection)、入射角を大きくしていった際に内部全反射が発生し始める入射角を臨界角$\hspace{2pt}\large{\theta_C}\hspace{2pt}$(Critical angle)といいます。
(全反射や臨界角については、別ページに詳しく解説しています。)