-光と光学に関連する用語の解説サイト-

屈折率とは

本項では、屈折率の定義や測定方法、複素屈折率について解説します。

1. 屈折率とは
2. 屈折率の測定方法
- 2-1. 最小偏角法
- 2-2. 臨界角法
3. 複素屈折率
- 3-1. 吸収係数$\large{\alpha}$と消衰係数$\large{\kappa}$の関係
- 3-2. 複素屈折率と比誘電率
参考文献

【1】屈折率とは

真空において光は$\large{c=2.998 \times 10^8}$[m/s]の速度で伝搬されます。
一方、物質中を光が進行する場合は、物質中の原子と相互作用を起こし、光の伝搬する速度は遅くなります。

屈折率とは、真空中での光速と、物質中を伝搬する光速(位相速度)の比によって定義される値です。
数式では、物質の屈折率を$\large{n}$、真空における光速を$\large{c}$、物質中の光速を$\large{v}$とすると、以下のように書き表せます。

【屈折率の定義】

$\large{ \displaystyle n = \frac{c}{v}\hspace{20pt}(1)}$

【1-1】相対屈折率と絶対屈折率

2つの物質の屈折率の比を取った値を相対屈折率といいます。
屈折率$\large{n_1}$の物質に対する、屈折率$\large{n_2}$の物質の相対屈折率は、$\large{\displaystyle n_{12}=\frac{n_2}{n_1}}$と表記します。

また、屈折率$\large{n_1}$を1としたときの相対屈折率を、絶対屈折率といいます。
屈折率$\large{n_1=1}$は真空中の屈折率であるため、絶対屈折率は真空に対する屈折率の大きさを表します。

通常、単に"屈折率"と書く場合には、この絶対屈折率の方を意味します。(本項でも"屈折率"と表記している場合は、絶対屈折率を意味します。)

【1-2】種々の物質の屈折率

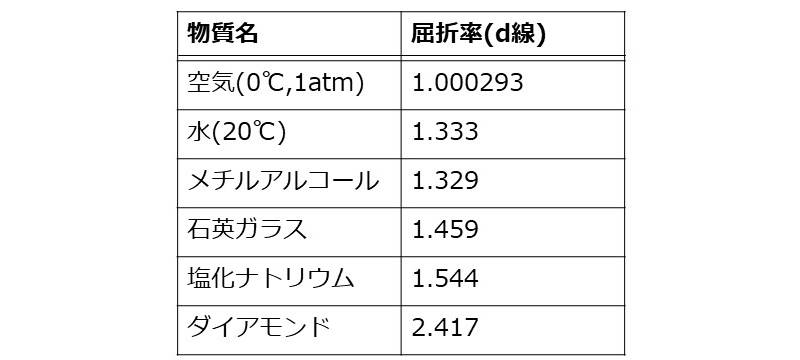
屈折率は物質により異なる値を持ちます。下記の表に種々の物質のd線(589.3nm)における屈折率を示します。

表1.種々の物質のd線(589.3nm)における屈折率

【1-3】屈折率の波長分散

物質の屈折率は、光の波長に依存して値が変化します。この波長によって屈折率が変化する現象を分散といいます。

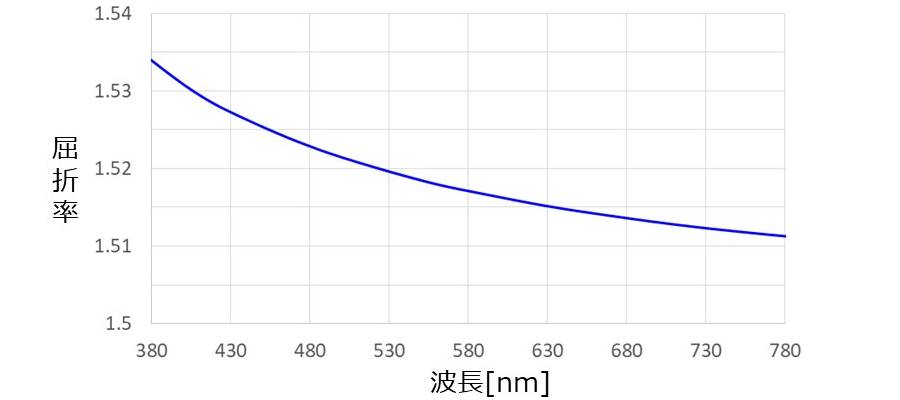
図1に、代表的な光学ガラスであるBK7の可視光域の波長(380～780nm)における屈折率の変化を示します。光学ガラスBK7の屈折率の波長依存性

図1.光学ガラスBK7の屈折率の波長依存性

分散は、プリズムに入射した白色光が色ごとに分離され虹色に見える現象や、レンズにより集光した白色光が色ごとに集光位置がずれる色収差の原因となります。

水やガラスなど多くの物質では、可視光域において波長が短いほど、屈折率が高いという関係にあります。 この関係にある場合、正常分散といいます。

一方、波長が短いほど、屈折率が低いという関係にある物質を、異常分散といいます。

ガラスなどの電子が自由に動けない物質の屈折率は、ローレンツモデルによってモデル化されます。
ローレンツモデルから、光が物質に吸収されない波長領域では正常分散、光が吸収される波長付近では異常分散となることが示されます。

ガラスが可視光線の範囲で正常分散であることは、可視光線の波長付近で光が物質に吸収されない(透明)であることに対応しています。

【2】屈折率の測定方法

屈折率の測定方法には、最小偏角法、臨界角法、Vブロック法などが知られています。
本章では、最小偏角法、臨界角法について測定方法を解説します。

【2-1】最小偏角法

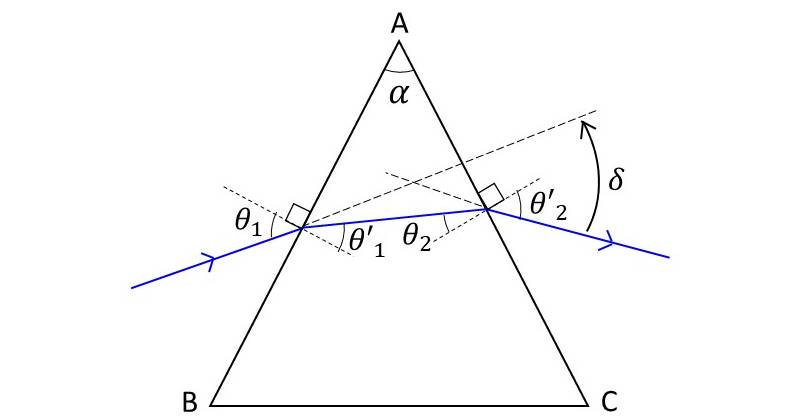
最小偏角法では、図2のような頂点の角度$\large{\alpha}$を持ったプリズムを使用して屈折率を測定します。最小偏角法の説明図

図2.最小偏角法の説明図

プリズムの屈折率をn,辺ABでの入射角と屈折角をそれぞれ$\large{\theta_1}$,$\large{\theta'_1}$、辺ACでの入射角と屈折角をそれぞれ$\large{\theta_2}$,$\large{\theta'_2}$とします。

入射光線と射出光線の角度の差分を偏角$\large{\delta}$といいます。最小偏角法は、この偏角$\large{\delta}$が最小となる値を求めることで、プリズムの屈折率nを求める測定方法です。

スネルの法則から、以下の関係が成り立ちます。 $$\large{\sin \theta_1 = n \sin \theta'_1 \hspace{20pt}(2)}$$ $$\large{n \sin \theta_2 = \sin \theta'_2 \hspace{20pt}(3)}$$

また、偏角$\large{\delta}$に関して以下の等式が成り立ちます。 $$\large{\delta = \theta_1 - \theta'_1 + \theta'_2 - \theta_2 \hspace{20pt}(4)}$$

幾何学的な関係から、プリズムの頂点$\large{\alpha}$と$\large{\theta'_1}$、$\large{\theta_2}$は以下のように表せます。 $$\large{\alpha = \theta'_1 + \theta_2 \hspace{20pt}(5)}$$

(4)、(5)式より、以下の関係が成り立ちます。 $$\large{\delta = \theta_1 + \theta'_2 -\alpha \hspace{20pt}(6)}$$

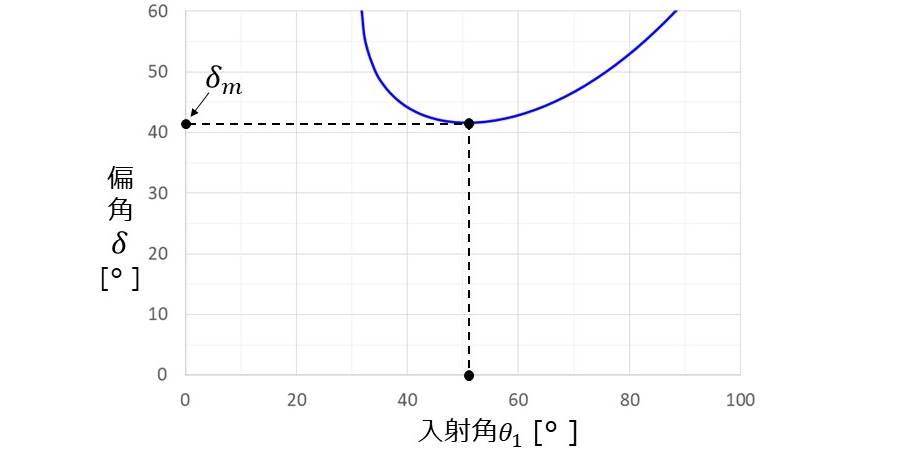
上式から、プリズムの入射角$\large{\theta_1}$と偏角$\large{\delta}$のグラフを描くと、図3のようになります。最小偏角法で測定される偏角の入射角依存性

図3.偏角$\large{\delta}$の入射角依存性(n=1.55,$\large{\alpha}$=60°)

偏角$\large{\delta}$が最小であるときを最小偏角$\large{\delta_m}$とします。
偏角が最小偏角$\large{\delta_m}$であるとき、$\large{\frac{d \delta}{d \theta_1}=0}$であることを条件に計算を行うと、$\large{\theta_1=\theta'_2}$、$\large{\theta'_1=\theta_2}$が導かれます。

このとき、(5),(6)式から以下の式を得ることができます。 $$\large{\delta_m = 2 \theta_1 -\alpha}$$ $$\large{\theta'_1 = \frac{\alpha}{2}}$$

(2)式より、屈折率nを求める式は以下のようになります。 $$\large{n=\frac{\sin \theta_1}{\sin \theta'_1} = \frac{\sin {((\delta_m + \alpha)/2)}}{\sin (\alpha/2)}}$$

以上より、最小偏角$\large{\delta_m}$とプリズムの頂点の角度$\large{\alpha}$から、プリズムの屈折率nが求められることが分かります。

補足【式の導出】

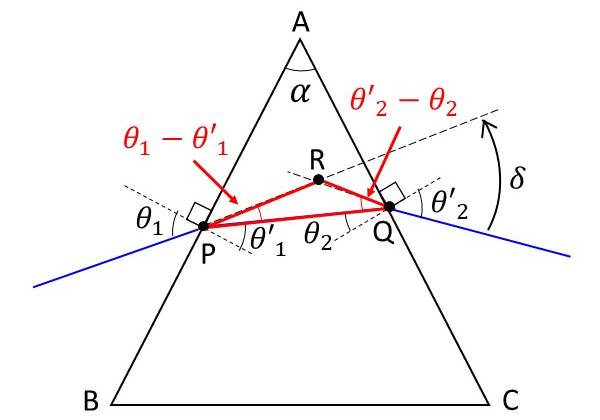
(4)式を導出するためには、図4の赤い三角形PQRに着目します。
$\large{\angle RPQ = \theta_1 - \theta'_1}$、$\large{\angle RQP = \theta'_2 - \theta_2}$となるため、$\large{\delta = \theta_1 - \theta'_1 + \theta'_2 - \theta_2}$が成り立ちます。最小偏角法の式の導出方法の説明図(1)

図4.(4)式の導出方法の説明図

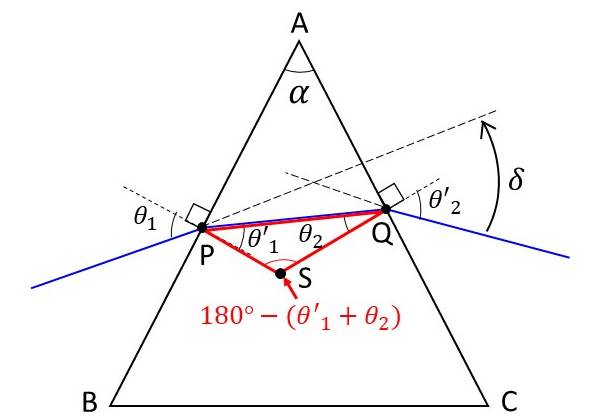
(5)式を導出するためには、まず図5の赤い三角形PSQに着目します。
図5より、角PSQの角度は$\large{\angle PSQ = 180^{\circ}-(\theta'_1 + \theta_2)}$となります。

また、四角形APSQに着目すると、辺ABと辺PS、辺ACと辺QSはそれぞれ直角であることから、角度$\large{\alpha}$と$\large{\angle PSQ}$の和が$\large{180^{\circ}}$となります。 $$\large{\alpha + (180^{\circ}-(\theta'_1 + \theta_2))=180^{\circ}}$$ したがって、(5)式が導かれます。 $$\large{\alpha = \theta'_1 + \theta_2}$$ 最小偏角法の式の導出方法の説明図(2)

図5.(5)式の導出方法の説明図

【2-2】臨界角法

屈折率の測定方法の１つである臨界角法(アッベ屈折計)では、プリズムからの射出角を測定することにより屈折率を求めます。

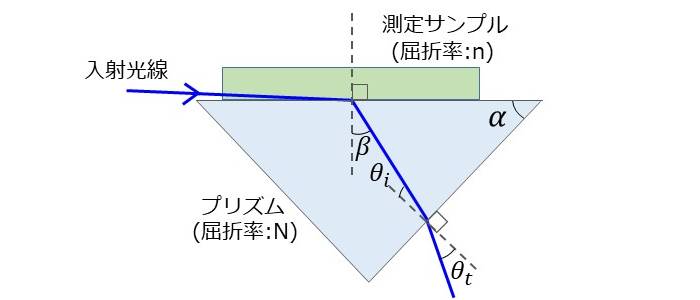
図6に臨界角法の光学系の概要を示します。屈折率の測定方法(臨界角法)

図6.臨界角法のイメージ

臨界角法では、プリズムに接するように測定サンプルを配置します。
測定サンプルとプリズムの境界面にほぼ平行に近い入射光を入射し、プリズムから射出される光を観察します。

測定サンプルとプリズムの境界面には、スネルの法則から以下の関係が成り立ちます。(入射角を90度とします。) $$\large{n = N \sin \beta}$$

プリズムの頂点の角度を$\large{\alpha}$とすると、プリズムの斜面への入射角$\large{\theta_i}$は以下のようになります。 $$\large{\theta_i = \alpha - \beta}$$

また、プリズムの斜面からの射出角$\large{\theta_t}$については、以下のようになります。 $$\large{ N \sin \theta_i = \sin \theta_t}$$ 以上の等式を解くと、以下の式が導かれます。プリズムからの射出角$\large{\theta_t}$を測定することにより、サンプルの屈折率$\large{n}$を求めることができます。

$$\large{n = \sin \alpha \sqrt{N^2 -\sin^2 \theta_t} + \sin \theta_t \cos \alpha} $$

【3】複素屈折率

複素屈折率とは、実部に光の伝搬速度を表す通常の屈折率$\large{n}$、虚部に光の吸収を表す消衰係数$\large{\kappa}$で表記をする値のことです。
吸収の存在する物質では、複素屈折率が使用されます。

【複素屈折率】

$\large{ \displaystyle \tilde{n} = n + i \kappa}$

【3-1】吸収係数$\large{\alpha}$と消衰係数$\large{\kappa}$の関係

複素屈折率の虚部である消衰係数$\large{\kappa}$は、単位長さ当たりの光エネルギーの吸収を表す吸収係数$\large{\alpha}$と関係があります。
z軸の正方向に波数$\large{k}$,角周波数$\large{\omega}$で進行する光の電場を以下のように表します。 $$\large{E(z,t)=E_0 e^{i(kz-wt)}}$$

ここで、複素屈折率を使用すると、波数$\large{k}$は以下のように書き表せます。 $$\large{k=\tilde{n} \frac{\omega}{c} = (n+i\kappa) \frac{\omega}{c}}$$

上記の波数$\large{k}$を(3)式に適用すると、以下の式を得ます。 \begin{eqnarray} \displaystyle E&=&E_0 e^{i(kz-wt)}\\ \displaystyle &=&E_0 e^{i(\tilde{n}\omega z/c-wt)} \\ \displaystyle &=&E_0 e^{-\kappa \omega z /c} e^{i(n\omega z/c-wt)}\hspace{20pt}(7)\\ \end{eqnarray}

(7)式から、複素屈折率の虚部$\large{\kappa}$が0でない場合(光の吸収が発生する場合)、光の電場$\large{E}$は距離$\large{z}$に対して指数関数で減少することが分かります。

光のエネルギーIは、電場の2乗の比例するため、(7)式から以下の式を得ます。 $$\large{I \propto {E_0}^2 e^{ -\frac{2 \kappa \omega}{c}z}}$$

吸収係数$\large{\alpha}$は、位置zに対して指数関数で減少する光エネルギーの指数部の係数にあたります。したがって吸収係数$\large{\alpha}$と消衰係数$\large{\kappa}$の関係は以下のようになります。 $$\large{\alpha = \frac{2 \kappa \omega}{c}}$$

【3-2】複素屈折率と比誘電率

光(電磁波)の伝搬を表現するマクスウェル方程式から、物質中を伝搬する光速は以下の式により与えられます。 $$\large{v = \frac{1}{\sqrt{\epsilon \mu}} = \frac{1}{\sqrt{\epsilon_0 \epsilon_r \mu_0 \mu_r}} }$$ $\large{\epsilon}$:誘電率, $\large{\epsilon_0}$:真空中の誘電率, $\large{\epsilon_r}$:比誘電率
$\large{\mu}$:透磁率, $\large{\mu_0}$:真空中の透磁率, $\large{\mu_r}$:比透磁率

真空中では、比誘電率$\large{\epsilon_r}$と比透磁率$\large{\mu_r}$は1になるため、真空中の光速は以下になります。 $$\large{c = \frac{1}{\sqrt{\epsilon_0 \mu_0}}}$$

したがって、屈折率$\large{n}$は以下のように表せます。

【屈折率】

$\large{ \displaystyle n = \frac{c}{v} = \sqrt{\epsilon_r \mu_r}}$

通常の物質は、可視光域における周波数で比透磁率は$\large{\mu_r=1}$となるため、屈折率$\large{n}$は比誘電率$\large{\epsilon_r}$により表されます。 $$\large{n = \sqrt{\epsilon_r}}$$

ここで、屈折率$\large{n}$が複素屈折率$\large{\tilde{n}}$で表されるとき、比誘電率も複素数により表されます。比誘電率$\large{\tilde{\epsilon_r}}$の実部を$\large{\epsilon_1}$、虚部を$\large{\epsilon_2}$と表記します。 $$\large{\tilde{\epsilon_r} = \epsilon_1 + i \epsilon_2}$$

上式から、複素屈折率と比誘電率の関係は$\large{\tilde{n} = \sqrt{\tilde{\epsilon_r}}=\sqrt{\epsilon_1 + i \epsilon_2}}$となります。複素屈折率は$\large{ \tilde{n} = n + i \kappa}$であることから、屈折率$\large{n}$と消衰係数$\large{\kappa}$を比誘電率の実部$\large{\epsilon_1}$と虚部$\large{\epsilon_2}$により表すと以下のようになります。

【屈折率と消衰係数】

$$\large{ \displaystyle n = \frac{1}{\sqrt{2}} \sqrt{\epsilon_1 + \sqrt{{\epsilon_1}^2 + {\epsilon_2}^2}}}$$ $$\large{ \displaystyle \kappa = \frac{1}{\sqrt{2}} \sqrt{ -\epsilon_1 + \sqrt{{\epsilon_1}^2 + {\epsilon_2}^2}} }$$

もしくは、$\large{\epsilon_1}$、$\large{\epsilon_2}$について解くと、以下のようになります。 $$\large{\epsilon_1 = n^2 - \kappa^2}$$ $$\large{\epsilon_2 = 2n \kappa}$$

屈折率$\large{n}$と、光の吸収を表す消衰係数$\large{\kappa}$が、１つの値$\large{\epsilon_r}$の実部と虚部により表現されることが分かります。
クラマース・クローニッヒの関係式はこの関係を利用しており、反射スペクトル測定から吸収スペクトルを算出するといった計算に利用されます。