光の干渉とは
本項では、以下の内容について解説しています。
- ・光の干渉の性質
- ・干渉縞の光強度の計算
- ・干渉縞の明暗の条件
【1】光の干渉とは
本章では、光の干渉とは何かについて解説します。
まず最初に『水面の波による干渉』について説明します。
次に、『水面の波の干渉』と『光の干渉』の違いから、光の干渉に特有な性質について解説します。
【1-1】水面の波の干渉
水面のある位置を上下に揺らすと、水面の波は同心円状に広がっていきます。
図1のように、水面を上下に揺らす2つの波源\(\large{S_1, S_2}\)が存在した場合、波源からの波は重なり合い、大きく振動する箇所と振動が打ち消し合う箇所が発生します。
このように振動の強め合いや弱め合いが発生する現象を干渉といいます。
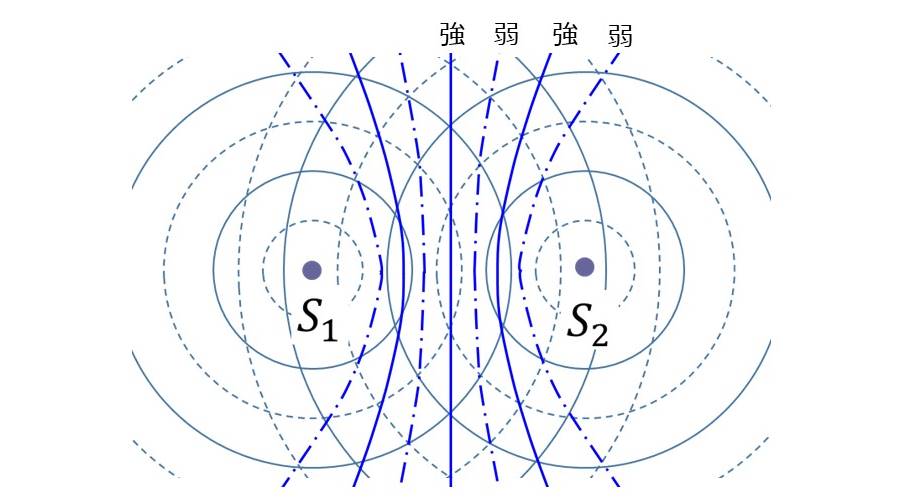
水面の波の一つ目の特徴として『干渉による振動の強め合い、弱め合いが波の高さとして観測できる』という点があります。
また、二つ目の特徴として『水面の2箇所を同時に振動させることで、簡単に干渉を発生させることができる』という点があります。
【1-2】光の干渉の性質 | 干渉縞の見え方
光の干渉を観察する実験は数多くありますが、本章ではヤングの実験を例として解説します。
ヤングによる光の干渉の実験は、図2のような実験系で行われました。
まず、光源からの光を単スリットに通した後、2つのスリットによって光を分割します。分割された光は干渉することにより、スクリーン上に明暗の縞模様を映し出します。
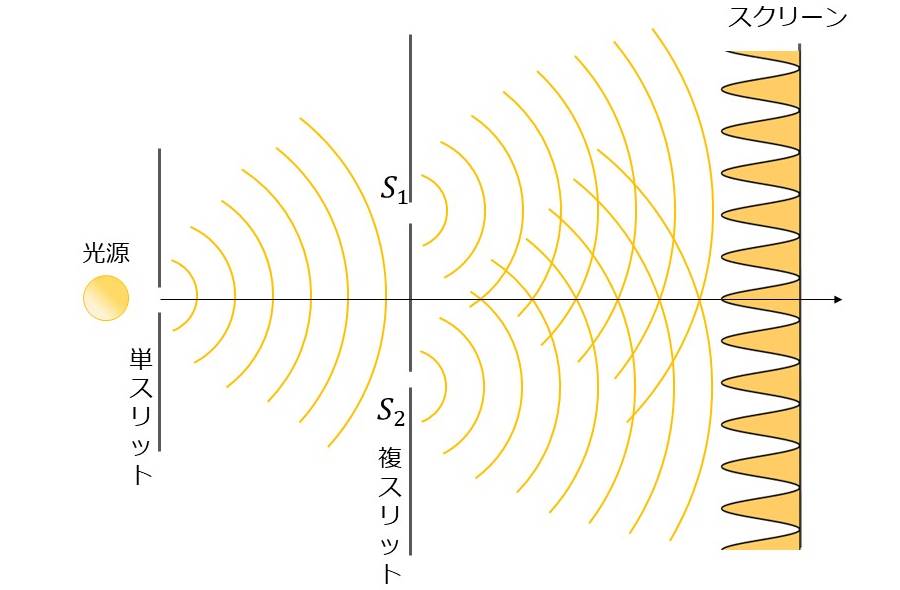
『光の干渉』と『水面の波の干渉』の違いの一つとして、干渉現象がどのように観察されるかという点があります。
先述したように、水面の波には『干渉による振動の強め合い、弱め合いが波の高さとして観測できる』という点があります。
一方、光の干渉は、空間を振動しながら伝わる電場の波が、干渉することにより発生します。
ここで、電場は可視光の波長領域では、約\(\large{10^{14}[Hz]}\)(1秒間に100兆回)で振動するため、干渉した電場そのものを直接的に観測することはできません。
そのため、光の干渉では『干渉による電場の振動の強め合い、弱め合いが、時間平均された明るさの強弱として観察する』ことになります。(光の干渉の光強度の計算については後述しています。)
水面の波の振動では、波の振動が直接的に観測できるため、時間とともに波が上下する様子が観測できます。
一方、光の干渉では、時間平均された明るさが観測されるため、時間が経過しても、強め合う箇所は明るいまま、弱め合う箇所は暗いまま、という状態で観測されます。
また、光の干渉の結果は明るさとして観察されるため、スクリーンなどに明るさを映し出して観察することになります。
例えば、図2のヤングの実験では、スクリーンに光の明るさの強弱を映すことにより光の干渉を観察しています。 (ニュートンリングや薄膜の干渉などは、人の目の網膜をスクリーンとして映し出していると考えられます。)
【1-3】光の干渉の性質 | コヒーレンス(可干渉性)
前章で説明した『光の干渉は電場が時間平均されて、明るさとして観察される』ことから、コヒーレンス(可干渉性)という光の干渉に特徴的な性質が説明されます。
先述したように、水面の波の特徴として『2箇所の水面を上下に揺らすことで簡単に干渉を観測することができる』という点があります。
一方、光の場合は、『2つの照明の光を重ね合わせただけでは、干渉現象を観察することはできない』という特徴があります。
この理由は、太陽光や照明の光などは多数の原子からの発光が元になっており、波の振れ幅や位相がランダムに変化してしまうため、干渉の効果を打ち消してしまうためです。
このような干渉を起こさない光同士をインコヒーレントといいます。
そこで、光の干渉を観測する方法として、1つの光源から放出された光を分割し、分割された光同士を重ね合わせることにより干渉を観測します。
つまり、光を自分自身と干渉させることによって、ランダムに振れ幅や位相が変化しまっても、干渉を引き起こせるようにします。
例えば、図2のヤングの実験が最初に行われたときは、太陽光の光を2つのスリットで分割し、スクリーン上で重ね合わせることで干渉を観測しています。
現代の干渉の実験では、自然光よりも振れ幅や位相の揺らぎの少ないレーザー光を利用することで、より鮮明な干渉縞を発生させています。
【2】光の干渉縞の計算
本章では、2つの光波が干渉したときの干渉縞の光強度の計算方法について解説します。
以下の式で表される光の電場\(\large{E_1,E_2}\)が、干渉する場合について考えます。(以下のような波の式については別ページで解説しています。) \begin{eqnarray} \large E_1&=& \large A_1 \exp [i( \boldsymbol{k_1} \cdot \boldsymbol{r} -\omega t+\phi_1)]\\ \large E_2&=& \large A_2 \exp [i( \boldsymbol{k_2} \cdot \boldsymbol{r} -\omega t+\phi_2)] \end{eqnarray}
\(\large{A_1, A_2}\)は光の電場の振れ幅、\(\large{\boldsymbol{k_1}, \boldsymbol{k_2}}\)は波数ベクトル、\(\large{\omega}\)は各周波数です。
\(\large{\phi_1,\phi_2}\)は光の電場の初期位相を表します。
【2-1】干渉縞の光強度
前述したように、水面を伝わる波の場合、波の振動をそのまま足し合わせた量が観測される波になります。
一方、光の場合は、干渉の結果が電場\(\large{E}\)の大きさではなく、光強度\(\large{I}\)として観測されます。
光強度\(\large{I}\)は、電場\(\large{E}\)の2乗に比例するとして計算することができます。
電場\(\large{E_1,E_2}\)がコヒーレント(位相、振れ幅などに揺らぎのない状態)であるとすると、光強度\(\large{I}\)は、以下のように求められます。 \begin{eqnarray} \large I&\propto& \large |E|^2\\ &=&\large |E_1 + E_2|^2\\ &=&\large {A_1}^2 + {A_2}^2 + 2 A_1 A_2 \cos(\delta)\hspace{10pt}(1) \end{eqnarray}
ここで、\(\large{\delta}\)は、電場\(\large{E_1,E_2}\)の位相差を表します。 $$\large{\delta = \boldsymbol{k_1} \cdot \boldsymbol{r} - \boldsymbol{k_2} \cdot \boldsymbol{r} +\phi_1 - \phi_2}\hspace{10pt}(2)$$
(1)式の第1項(\(\large{{A_1}^2}\))と第2項(\(\large{{A_2}^2}\))は、光が単独で存在しているときの光強度に等しくなります。
第3項の\(\large{2 A_1 A_2 \cos(\delta)}\)が、光の干渉による光強度の変化を表す項です。
また、\(\large{\phi_1 - \phi_2}\)は電場\(\large{E_1,E_2}\)の初期位相の差分を表します。
この初期位相\(\large{\phi_1 - \phi_2}\)が時間によってランダムに変化してしまうと、時間平均を取ったときに\(\large{\cos \delta}\)の成分がゼロとなり、干渉縞が発生しません。
前述した2つの照明の光を重ね合わせても干渉縞が発生しない状況が、初期位相\(\large{\phi_1 - \phi_2}\)がランダムに変化するときに相当します。
ここで、(1)式から、光強度が最大のときの光強度\(\large{I}\)は\(\large{\cos(\delta)=1}\)より、\(\large{I \propto (A_1 + A_2)^2}\)となります。
特に、干渉する2つの光の強度が等しい場合(\(\large{A=A_1 = A_2}\))のとき、光強度\(\large{I\propto{4A}^2}\)となります。
また、弱め合うときの光強度は、\(\large{I\propto (A_1 - A_2)^2}\)となります。特に、干渉する2つの光の強度が等しい場合(\(\large{A_1 = A_2}\))のとき、光強度は\(\large{I=0}\)となります。
【2-2】干渉縞の光強度の計算例
ここで、図3に示すヤングの実験を例に、干渉縞の光強度の計算を行います。
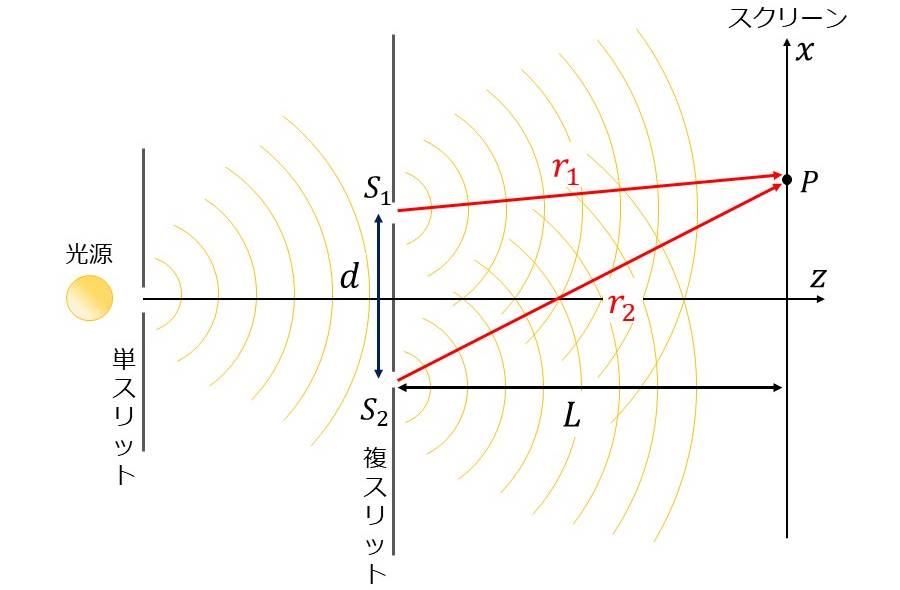
図3の複スリットで、光強度が均等に分割されているとすると、(1)式で\(\large{A_1 = A_2}\)が成り立ちます。
したがって、電場の振幅を\(\large{A=A_1=A_2}\)として、(1)式を変形します。 \begin{eqnarray} \large I&\large \propto&\large 2A^2(1+\cos(\delta))\\ &\large =&\large 4A^2 \cos^2 \frac{\delta}{2}\hspace{10pt}(1')\\ \end{eqnarray}
(1')の\(\large{\delta}\)が2つの光波の位相差を表しています。ここで、位相差\(\large{\delta}\)の具体的な式を求めます。
図3から複スリットからスクリーン面までの距離\(\large{r_1}\)、\(\large{r_2}\)は、以下の式により求められます。 $$\large{r_1 = \sqrt{{L}^2+{\left(x-\frac{d}{2}\right)}^2}}$$ $$\large{r_2 = \sqrt{{L}^2+{\left(x+\frac{d}{2}\right)}^2}}$$
複スリットからスクリーンまでの距離\(\large{r_0}\)が、スリット間隔\(\large{d}\)より十分大きいとすると、以下の近似が成り立ちます。 $$\large{r_1 \approx L + \frac{1}{2} \frac{{(x - \frac{d}{2})}^2}{L}}$$ $$\large{r_2 \approx L + \frac{1}{2} \frac{{(x + \frac{d}{2})}^2}{L}}$$
分割された光の位相差\(\large{\delta}\)は、複スリットからスクリーン面までの距離\(\large{r_1}\)、\(\large{r_2}\)から以下の式により求められます。 $$\large{\delta = k(r_2 - r_1)=\frac{2 \pi}{\lambda}(r_2 -r_1)}\hspace{10pt}(2')$$ (\(\large{k}\)は波の波数を意味し、\(\large{k=\frac{2 \pi}{\lambda}}\)の関係があります。)
上式から位相差\(\large{\delta}\)を求めると以下のようになります。 \begin{eqnarray} \large \delta&\large =&\large \frac{2 \pi}{\lambda}(r_2 -r_1)\\ &\large =&\large \frac{2 \pi}{\lambda} \frac{{\left(x+\frac{d}{2}\right)}^2 - {\left(x-\frac{d}{2}\right)}^2}{2L}\\ &\large =&\large \frac{2 \pi xd}{\lambda L} \end{eqnarray}
したがって、光強度\(\large{I}\)の式(1')に代入すると、以下の干渉縞の光強度の式を得ることができます。 $$\large {I \propto 4A^2 \cos^2 \frac{\delta}{2} = 4A^2 \cos^2 \frac{\pi xd}{\lambda L} }$$
【3】光の干渉の『強め合いの条件』と『弱め合いの条件』
干渉の式(1)から、干渉縞の光強度は2つの光の位相差\(\large{\delta}\)によって周期的に変化することが分かります。
本章では、観測される干渉縞の強め合う条件と弱め合う条件を求めます。
・光の干渉の強め合いの条件
干渉の式(1)から、干渉縞の光強度は\(\large{\cos \delta}\)の項により周期的に変化するため、位相差\(\large{\delta}\)が\(\large{2 \pi}\)の整数倍であるとき、観測される干渉縞が最大となります。
\(\large{\displaystyle \delta = \pm 2m \pi \hspace{10pt} (m=0,1,2,\cdots)}\hspace{10pt}(3)\)
また、(2)式から同じ波長\(\large{\lambda}\)の光が光路差\(\large{d_2 - d_1}\)で重なるとき、位相差\(\large{\delta}\)は以下のように表されます。
$$\large{\delta = k(d_2 - d_1)=\frac{2 \pi}{\lambda}(d_2 - d_1)}$$
(\(\large{k}\)は波の波数であり、\(\large{k=\frac{2 \pi}{\lambda}}\)の関係があります。)
したがって、波長\(\large{\lambda}\)と光路差\(\large{d_2 - d_1}\)を使用して強め合いの条件を導くと、以下のようになります。
\(\large{\displaystyle d_2 - d_1 = \pm m \lambda \hspace{10pt} (m=0,1,2,\cdots)}\hspace{10pt}(3')\)
高校物理では、干渉縞の強め合う条件は『光路差が波長の整数倍の場合に強め合う』という意味の(4')式で学習するため、(3')式の形式の方が慣れている人が多いと思います。
ヤングの実験や薄膜の干渉など、多くの干渉現象では光の伝搬する光路長の差分から干渉が発生するため、(3')の式で問題ありません。
一方、平面波の干渉では、平面波が角度をもって交わることで位相差が発生し、干渉縞が発生します。この場合、干渉縞の強め合う条件は、(3)式の『位相が\(\large{2 \pi}\)の整数倍の場合に強め合う』ことから計算します。
・光の干渉の弱め合いの条件
一方、位相差\(\large{\delta}\)が\(\large{\pi}\)の奇数倍であるとき、観測される干渉縞の光強度は最小となります。
\(\large{\displaystyle \delta = \pm (2m+1) \pi \hspace{10pt} (m=0,1,2,\cdots)}\)
強め合いの場合と同様に、同じ波長\(\large{\lambda}\)の光が光路差\(\large{d_2 - d_1}\)で重なるときの弱め合いの条件は以下のようになります。
\(\large{\displaystyle d_2 - d_1 = \pm \left(m+\frac{1}{2} \right) \lambda \hspace{10pt} (m=0,1,2,\cdots)}\)