平面波の干渉

本項では、以下の内容について解説しています。

• ・平面波の波数ベクトル
• ・平面波の干渉による光強度
• ・平面波の干渉による縞の間隔

【1】平面波の干渉

平面波がなす角\(\hspace{2pt}\large{2\theta}\hspace{2pt}\)で交わっているときに発生する光の干渉縞について解説します。

【1-1】平面波の波数ベクトル

図1のように、同じ周波数と波長であり、互いにコヒーレントである平面波\(\hspace{2pt}\large{E_1}\hspace{2pt}\)、\(\hspace{2pt}\large{E_2}\hspace{2pt}\)が、y軸方向に対してなす角\(\hspace{2pt}\large{2\theta}\hspace{2pt}\)で交わっているとします。このときにx軸上に生成される干渉縞について考えます。

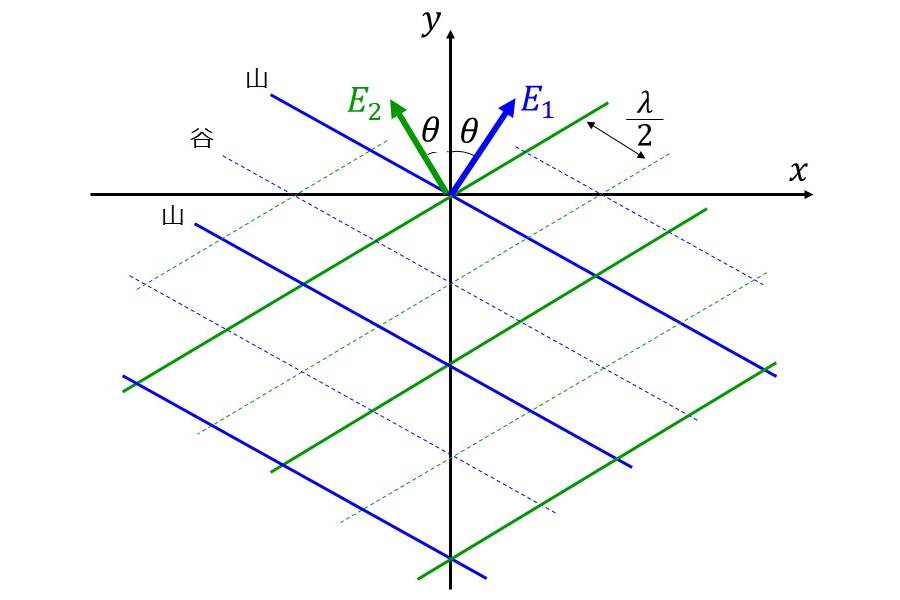
平面波\(\hspace{2pt}\large{E_1}\hspace{2pt}\)、\(\hspace{2pt}\large{E_2}\hspace{2pt}\)が以下のように書き表せるとします。\(\hspace{2pt}\large{A_1,A_2}\hspace{2pt}\)は電場の振れ幅、\(\hspace{2pt}\large{\boldsymbol{k_1},\boldsymbol{k_2}}\hspace{2pt}\)は波数ベクトル、\(\hspace{2pt}\large{\omega}\hspace{2pt}\)は角周波数を表します。また、\(\hspace{2pt}\large{\phi_1,\phi_2}\hspace{2pt}\)は平面波の初期位相を表します。

\begin{eqnarray} \large E_1&=& \large A_1 \cos ( \boldsymbol{k_1} \cdot \boldsymbol{r} -\omega t + \phi_1)\\ \large E_2&=& \large A_2 \cos ( \boldsymbol{k_2} \cdot \boldsymbol{r} -\omega t + \phi_2) \end{eqnarray}

ここで、上式の平面波\(\hspace{2pt}\large{E_1}\hspace{2pt}\)、\(\hspace{2pt}\large{E_2}\hspace{2pt}\)の波数ベクトルの絶対値が\(\hspace{2pt}\large{k}\hspace{2pt}\)で等しいとします。 $$\large{|\boldsymbol{k_1}|=|\boldsymbol{k_2}|=k}$$

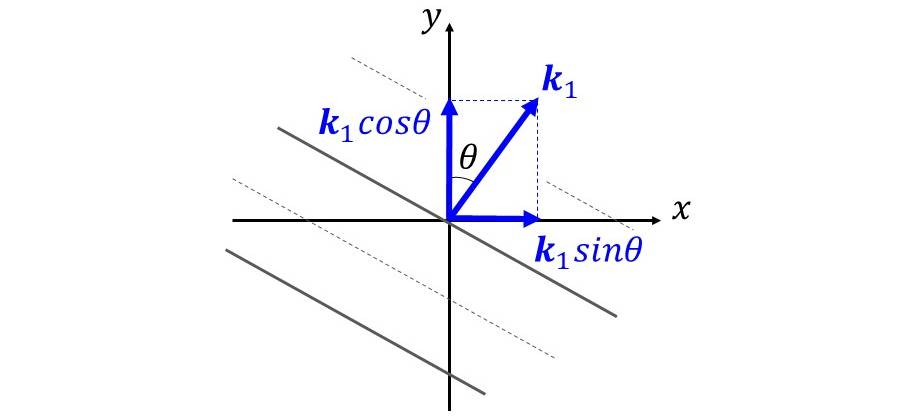
このとき、図2より波数ベクトルは、y軸に対する角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)を用いてx方向とy方向の成分ごとに表されます。 \begin{eqnarray} \large \boldsymbol{k_1}&=& \large (k \sin \theta, k \cos \theta)\\ \large \boldsymbol{k_2}&=& \large (-k \sin \theta, k \cos \theta) \end{eqnarray}

したがって、平面波\(\hspace{2pt}\large{E_1}\hspace{2pt}\)、\(\hspace{2pt}\large{E_2}\hspace{2pt}\)の位相項\(\hspace{2pt}\large{\boldsymbol{k_1} \cdot \boldsymbol{r}}\hspace{2pt}\)と\(\hspace{2pt}\large{\boldsymbol{k_2} \cdot \boldsymbol{r}}\hspace{2pt}\)をx成分、y成分に分解すると以下の式のようになります。

\begin{eqnarray} \large \boldsymbol{k_1} \cdot \boldsymbol{r}&=& \large k \sin \theta \cdot x + k \cos \theta \cdot y\\ \large \boldsymbol{k_2} \cdot \boldsymbol{r}&=& \large -k \sin \theta \cdot x + k \cos \theta \cdot y \end{eqnarray}

【1-2】平面波による干渉縞の光強度

ここで、互いにコヒーレントである2つの平面波による干渉縞の光強度\(\hspace{2pt}\large{I}\hspace{2pt}\)は、以下の式で計算されます。(干渉縞の光強度は干渉とはの記事で解説しています。)

干渉の光強度\(\hspace{2pt}\large{I}\hspace{2pt}\)を表す(1)式に、前章の平面波の波数ベクトルの計算結果を使うと、以下のようになります。

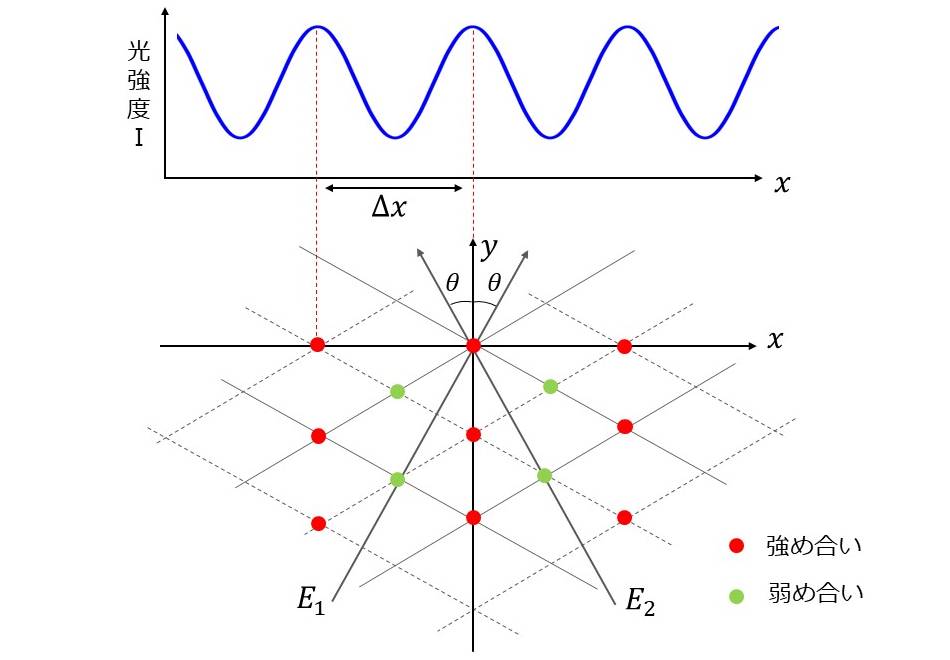
(2)式により、平面波の干渉の光強度\(\hspace{2pt}\large{I}\hspace{2pt}\)は位置xを変数として縞の明暗が発生することを表します。図3上に、x軸に沿ってスクリーンを置いたときに観測される光強度を図示します。

なお、図3の干渉縞の光強度\(\hspace{2pt}\large{I}\hspace{2pt}\)は、\(\hspace{2pt}\large{\phi_1 = \phi_2}\hspace{2pt}\)の場合を図示しています。\(\hspace{2pt}\large{\phi_1 \neq \phi_2}\hspace{2pt}\)である場合は、初期位相の差分だけx軸方向に平行移動した干渉縞となります。

図3下には、ある時刻における平面波同士の強め合いの位置と弱め合いの位置を示します。赤点が強め合う点、緑点が弱め合う点を表します。

【1-3】平面波による干渉縞の間隔

(2)式から、\(\hspace{2pt}\large{\cos(2 k \sin \theta \cdot x +\phi_1 - \phi_2) =1}\hspace{2pt}\)であるとき、平面波の干渉縞の光強度\(\hspace{2pt}\large{I}\hspace{2pt}\)が最大となります。
したがって、以下を満たす位置\(\hspace{2pt}\large{x}\hspace{2pt}\)において干渉縞の強度が最大となることが分かります。

ここで、上式から\(\hspace{2pt}\large{m+1}\hspace{2pt}\)番目と\(\hspace{2pt}\large{m}\hspace{2pt}\)番目の縞の位置の差分を計算することで、干渉縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)を求めることができます。 \begin{eqnarray} \large \Delta x&=&\large x_{m+1}-x_{m}\\[0.5em] &=&\large \frac{\pi}{k \sin \theta}\\[0.5em] &=&\large \frac{\lambda}{2 \sin \theta} \end{eqnarray}

上式から、平面波の干渉縞の間隔\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)は、平面波とy軸のなす角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)と波長\(\hspace{2pt}\large{\lambda}\hspace{2pt}\)により決まることが分かります。

平面波とy軸のなす角\(\hspace{2pt}\large{\theta}\hspace{2pt}\)を小さくすると、干渉縞の間隔が広がります。
平面波を完全に同じ方向(\(\hspace{2pt}\large{\theta=0}\hspace{2pt}\))としてしまうと、\(\hspace{2pt}\large{\Delta x}\hspace{2pt}\)が無限大となり干渉縞が観測できなくなることが分かります。

また、角度\(\hspace{2pt}\large{\theta}\hspace{2pt}\)を大きくすると、縞の間隔は狭くなります。平面波が直角に交わる\(\displaystyle\hspace{2pt}\large{\theta=\frac{\pi}{2}}\hspace{2pt}\)で最小値\(\displaystyle\hspace{2pt}\large{\Delta x = \frac{\lambda}{2}}\hspace{2pt}\)となります。

---